标签：
1.向量空间和子空间
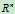:包含所有n维的列向量（之所以使用R：列向量的元素都是实数）
在所有向量空间内都支持的操作：
实数向量空间：
8个规则：
用的较多的还是向量空间和子空间的定义，即乘法和加法的结果仍在集合内。子空间也是向量空间
相反的方面，若一个集合不能构成向量空间，则这个集合的元素相加或相乘的结果可能不在这个集合内。
子空间：
零向量是任何向量空间的子空间。
最小的子空间仅由一个向量构成：0向量。称作0维空间。向量空间不允许是空集。
最大的子空间就是原始的向量空间本身。
3维空间的子空间：
子空间可以缩小维度（由上图），但实质都是从原始空间点集抽出的一个子集和，集合中的元素都来自原始集合。
列向量空间：
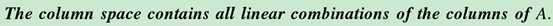
注意向量空间的原子是‘列‘（概念上的列，列实际可以是各种形式，如一个函数，一个矩阵）。
方程解与列向量空间的联系：
对于
Ax = b can be solved if and only if b lies in the plane that is spanned（标定） by the two column vectors .这个plane就是A的列向量空间，同时也是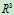
的子空间（过0点）。这个plane是
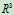的子空间的证明 p89
C（A）：A的列向量空间，是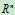
的子空间，证明p89。注意
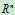是我们讨论各种问题所在的全集，就类似与1属于自然数n这种关系。
N（A）：A的nullspace，是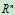
的子空间,证明：
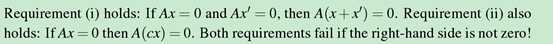
x+x‘在nullspace内，cx也在nullspace内，所以x的全集是
的子空间
注意一开始用
举线性组合的例子，A里只有两列(这种情况就高斯消元法来讲一定是奇异的情况，pivots个数不够)
Nullspace:
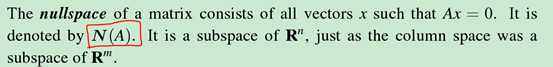
注意：之前说的向量空间都是由b直接构成，nullspace似乎不是这样，它是由构成0向量空间的线性组合的系数构成的，有点区别
了解C(A)和N(A)的目的：
问题集合：
的子空间由四种类型：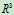
本身，面，线，零。
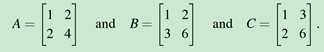
[??]B的列向量空间已经和A的不同了，列向量空间和解是什么关系呢？C的列向量空间仍和A一致。
列向量空间和nullspace的关系，进一步和complete solution的关系，见一下节，在解方程的时候做基本变换虽然改变了列向量空间，但是解是没有变的。
4.a能由两个向量唯一确定，但是不能由三个向量唯一确定
.
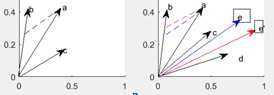
c和d可以确定任意多个向量如e和e‘,e在和b确定a.
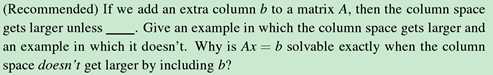
除非b在A的向量空间内，由上面第二图可知，添加了一个仍在A的向量空间内的d仍是可解的。
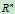
2.解Ax=0和Ax=b
对于可逆矩阵来说，Ax=0的解只有x=0,Ax=b对于任意b都有解。当nullspace里出现了非零解或者A的列向量空间小于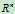
是我们这节要处理的情况。
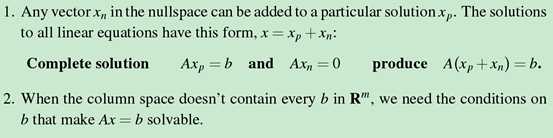
梯队形式（echelon form）：
因为我们使用消元法获得U，将之按照相反的过程还原，自然可以得到原来的矩阵A，因此：
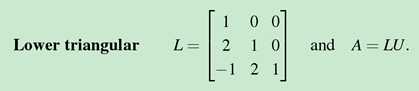
L是方阵，行数等于A和U的行数
PA=LU是一般形式：
获取R: 1.将U的pivots化成0 2.从下往上将pivots正上方的元素化成0，如下：
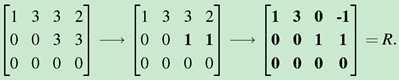
* matlab里获取R R=rref(A)，对于可逆矩阵，R=I
上章中是PA=LDU，Gauss-Jordan方法中[A I]->[U L逆]->[I A逆]，涉及A->U,pivots上方元素化0等，求R的方法和这两个方法神似。
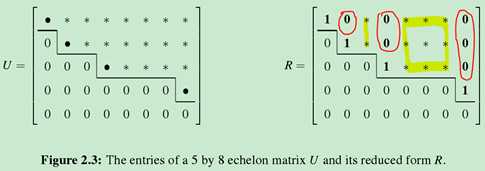
R still contains an identity matrix.in the pivot rows and pivot columns.
Rx=0 Ux=0 Ax=0 具有相同的解。
pivot variables: variables(in vector x) correspond to columns with pivots
Free variables: variables(in vector x) correspond to columns without pivots
从下面可以看出，在对x的表示中pivot varialbes全部由free variables表示了。而free variables之所以叫free variables，是因为这些变量是可以任意取值的。
运用R求Ax=0:
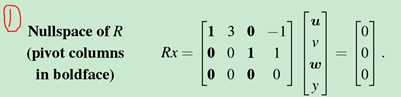
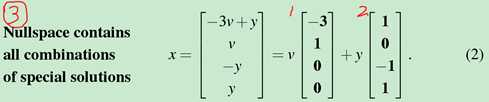
Special solutions for Ax=0:就是③中右侧的每一列是一个special solutions.
A的nullspace可以看成special solutions的combination的集合
在上例中，A的nullspace是 2维 的向量空间。
注意：仔细观察，special solutions的个数等于free variables的个数
对于A（m by n,n>m）来说，至少有n-m个free variables.
一个非常重要的结论：
从解Rx=0的过程可知，每多出一个free variables,就会多出一个special solution,对于A（m by n,n>m）来说，至少有n-m个free variables，这也是得出2C的原因。又因为free variables可以任意取值，所以解的个数是无限个。
Solving Ax = b, U x = c, and Rx = d
和Ax=0中不同的一点：即使n>m（more unkonwns than equations）,也不一定有解。主要是方程右边的b!=0造成了方程的平行（b=0的时候方程重合）。
讲解这个问题的顺序：先找到一个使方程有解的b,主要使用了b应该在列向量空间的方法。使用与上节相同的方法找到方程的解（利用free variables和pivot variables）得出结论。
求Ax=b:
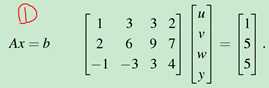
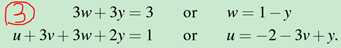
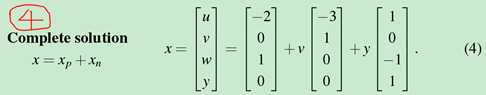
结论：
Every solution to Ax = b is the sum of one particular solution and a solution to Ax = 0:
关于
，可以将b看成0+b,按照上节方法b=0的部分的解为
，b=b的部分的解为
。
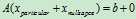。（由现象到结论，这是一种推广）
当b=0时也有特解，只不过特解是0.
将Ax=b化成Rx=d之后就可以直接得出结论，注意这个方法，连同上一节的直接获取结果的方法：
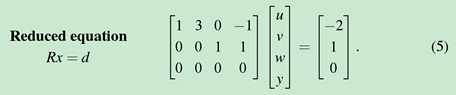
D中值对应到pivot variable对应位置的特解，特解中free variable对应位置为0.free variable对应到special solution里。
Rank of the matrix: 矩阵的秩
You see how the rank r is crucial. It counts the pivot rows in the "row space" and the
pivot columns in the column space. There are n − r special solutions in the nullspace.
There are m − r solvability conditions on b or c or d（之所以这么说，是因为剩下的m-r行决定方程是否有解）.
问题集合：
1.
方程无解的时候仍可以有nullspace,此时有Xn但是无Xp.
2.
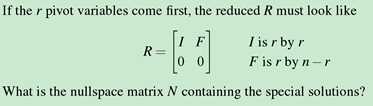ans: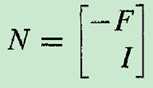
3.
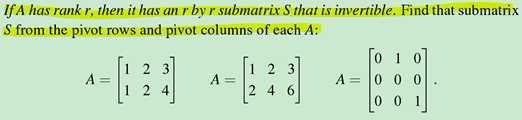
也就是说pivot columns所在的列是线性无关的列
4.[??]
小于A好证（AB的结果是A的线性组合，逃不出A所在的‘plane‘），小于B呢？
5.注意若AB=I,在AB不为方阵的时候也可以成立，定义左逆右逆的公式中都是指的方阵,不是方阵的情况下左逆不等于右逆（维数都不相同），逆的定义中是同时满足左逆右逆才叫逆。
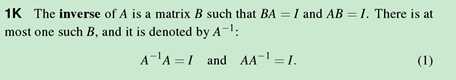
6.
7.[!!]
8. A system Ax=b has at most one particular solution:错。它的任意解都可以认做是一个特解。只要Xp+Xn=X成立就可以。
9.解的情况大概也就这么多了
（a）rows>rank(A),columns=rank(A) (b).rows=rank(A),columns>rows (c)rows>rank(A)，columns>rank(A) (d) invertible
10.
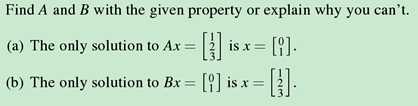
用上面的结论很容易就可以做出来：（a）秩为2且有解即是 （b）秩小于列数，无解或无限解。
11.
方程组相交成点，方程组中没有未知量，相交成线，有一个未知量，因此秩是3.
（b）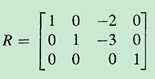
12. 处于后列的pivot variable是无法使用处于前列的free variable的。
13.why does no 3 by 3 matrix have a nullspace that equals its column space
可逆时：nullspace只有一个元素，column space为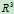
秩为2时：nullspace是线，column space是面
秩为1时：nullspace是面，column space是线
标签：
原文地址：http://www.cnblogs.com/wangxiaotao/p/5656631.html
