Fibonacci数列

标签：

Fibonacci数是组合数学中非常重要的一个数列，它的递推公式是：
　　F(1)=F(2)=1
　　F(n)=F(n-1)+F(n-2)
　　当然，用这个公式来计算F(n)是非常慢的，当计算F(n)时需要从F(1)一直计算到F(n)。Fibonacci数列还满足一些其他的公式，如：
　　F(a+b+1)=F(a+1)*F(b+1)+F(a)*F(b)
　　利用这个公式，可以加速Fibonacci数的计算。我们考虑同时计算F(2n+1)和F(2n)，则按照上面的公式：
　　F(2n+1)=F(n+1)*F(n+1)+F(n)*F(n)
　　F(2n)=F(n+1)*F(n)+F(n)*F(n-1)=F(n+1)*F(n)+F(n)*(F(n+1)-F(n))
　　这样，F(2n+1)和F(2n)的计算变为了F(n+1)和F(n)的计算，即下标变为了原来的一半。重复利用这种方法，可以每次让下标变为原来的一半，总共需要大约log n次计算(以2为底)。
　　当n较大时，后面的方法就比直接的递推要快得多，比如当n=1000000时，后面的方法大概需要20次计算，而直接递推的方法大概需要1000000次计算

Fibonacci的矩阵快速幂算法：

Fibonacci数列

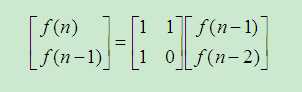
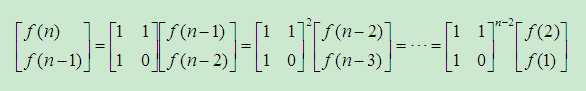
标签：

原文地址：http://www.cnblogs.com/FuTaimeng/p/5657724.html