标签：
难得有想法写一整套题解
首先想说的是，这场CF，我感觉是div2极为不错的一场(对于中档选手<因为我就出了三题，还掉了一个……
说笑了，感觉这一场很耐人寻味。就是那种抓破头皮想不出，知道做法后细细品味，有种 哦~~~~~这样啊~~~~好神奇！！！ 的感觉
首先。。秀一下战绩
不多说了 都在题里
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
While swimming at the beach, Mike has accidentally dropped his cellphone into the water. There was no worry as he bought a cheap replacement phone with an old-fashioned keyboard. The keyboard has only ten digital equal-sized keys, located in the following way:
Together with his old phone, he lost all his contacts and now he can only remember the way his fingers moved when he put some number in. One can formally consider finger movements as a sequence of vectors connecting centers of keys pressed consecutively to put in a number. For example, the finger movements for number "586" are the same as finger movements for number "253":
Mike has already put in a number by his "finger memory" and started calling it, so he is now worrying, can he be sure that he is calling the correct number? In other words, is there any other number, that has the same finger movements?
The first line of the input contains the only integer n (1?≤?n?≤?9) — the number of digits in the phone number that Mike put in.
The second line contains the string consisting of n digits (characters from ‘0‘ to ‘9‘) representing the number that Mike put in.
If there is no other phone number with the same finger movements and Mike can be sure he is calling the correct number, print "YES" (without quotes) in the only line.
Otherwise print "NO" (without quotes) in the first line.
3 586
NO
2 09
NO
9 123456789
YES
3 911
YES
You can find the picture clarifying the first sample case in the statement above.
题目大意是：给出一串电话号(长度<=10，保证不存在重复的数字，问存不存在号码，和该号码手指移动轨迹相同。
更直白的，给出一个锁屏，问存不存在其他锁屏密码跟改密码有同样的移动模式(例如0->9和8->6 移动方向 距离都一样
很多种做法，我稍微简化了一点点，记录每个数字上下左右。然后枚举移动方向和距离，将整个号码拖着移动。看看合不合法
跟头就是。。。方向有负，而我判断合法是用while。然后不断减减。。你懂得……
问我这样不会TLE么……TLE就好了，不至于FST……反正过了这题也会掉分 无所谓了=，= 没TLE‘多亏’我当时的特判……直接非法了……
半夜等到的FST。。一怒之下手机改代码A……改了哪里。。应该很容易看出来吧TOT
代码如下：
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <vector>
#define LL long long
#define Pr pair<int,int>
#define VI vector<int>
using namespace std;
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
char str[11];
int mp[10];
int to[4][10];
int n;
bool mv(int a,int x,int y)
{
int opt;
if(x > 0) opt = 0;
else opt = 1;
while(x)
{
if(to[opt][a] == -1) return false;
a = to[opt][a];
if(x>0)
x--;
else x++;
}
if(y > 0) opt = 2;
else opt = 3;
while(y)
{
if(to[opt][a] == -1) return false;
a = to[opt][a];
if(y>0)
y--;
else y++;
}
return true;
}
bool can(int x,int y)
{
bool f = 1;
for(int i = 0; i < n; ++i)
{
if(!mv(mp[i],x,y)) return false;
}
return true;
}
int main()
{
scanf("%d",&n);
scanf("%s",&str);
memset(to,-1,sizeof(to));
to[0][0] = 8;
for(int i = 4; i <= 9; ++i) to[0][i] = i-3;
to[1][8] = 0;
for(int i = 1; i <= 6; ++i) to[1][i] = i+3;
for(int i = 1; i <= 9; ++i)
{
if(i != 1 && i != 4 && i != 7) to[2][i] = i-1;
}
for(int i = 1; i <= 9; ++i)
{
if(i != 3 && i != 6 && i != 9) to[3][i] = i+1;
}
for(int i = 0; str[i]; ++i)
{
mp[i] = str[i]-'0';
}
for(int i = -3; i <= 3; ++i)
{
for(int j = -3; j <= 3; ++j)
{
if(i == 0 && j == 0) continue;
if(can(i,j))
{
puts("NO");
return 0;
}
}
}
puts("YES");
return 0;
}
Recently, Mike was very busy with studying for exams and contests. Now he is going to chill a bit by doing some sight seeing in the city.
City consists of n intersections numbered from 1 to n.
Mike starts walking from his house located at the intersection number 1 and goes along some sequence of intersections. Walking from intersection
number i to intersection j requires |i?-?j| units
of energy. The total energy spent by Mike to visit a sequence of intersections p1?=?1,?p2,?...,?pk is
equal to 
units
of energy.
Of course, walking would be boring if there were no shortcuts. A shortcut is a special path that allows Mike walking from one intersection to another requiring only 1 unit of energy. There are exactly n shortcuts in Mike‘s city, the ith of them allows walking from intersection i to intersection ai (i?≤?ai?≤?ai?+?1) (but not in the opposite direction), thus there is exactly one shortcut starting at each intersection. Formally, if Mike chooses a sequence p1?=?1,?p2,?...,?pk then for each 1?≤?i?<?k satisfying pi?+?1?=?api and api?≠?pi Mike will spend only 1 unit of energy instead of |pi?-?pi?+?1| walking from the intersection pi to intersection pi?+?1. For example, if Mike chooses a sequencep1?=?1,?p2?=?ap1,?p3?=?ap2,?...,?pk?=?apk?-?1, he spends exactly k?-?1 units of total energy walking around them.
Before going on his adventure, Mike asks you to find the minimum amount of energy required to reach each of the intersections from his home. Formally, for each 1?≤?i?≤?n Mike is interested in finding minimum possible total energy of some sequence p1?=?1,?p2,?...,?pk?=?i.
The first line contains an integer n (1?≤?n?≤?200?000) — the number of Mike‘s city intersection.
The second line contains n integers a1,?a2,?...,?an (i?≤?ai?≤?n ,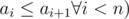 
,
describing shortcuts of Mike‘s city, allowing to walk from intersection i to intersection ai using
only 1 unit of energy. Please note that the shortcuts don‘t allow walking in opposite directions (from ai to i).
In the only line print n integers m1,?m2,?...,?mn, where mi denotes the least amount of total energy required to walk from intersection 1 to intersection i.
3 2 2 3
0 1 2
5 1 2 3 4 5
0 1 2 3 4
7 4 4 4 4 7 7 7
0 1 2 1 2 3 3
In the first sample case desired sequences are:
1:?1; m1?=?0;
2:?1,?2; m2?=?1;
3:?1,?3; m3?=?|3?-?1|?=?2.
In the second sample case the sequence for any intersection 1?<?i is always 1,?i and mi?=?|1?-?i|.
In the third sample case — consider the following intersection sequences:
1:?1; m1?=?0;
2:?1,?2; m2?=?|2?-?1|?=?1;
3:?1,?4,?3; m3?=?1?+?|4?-?3|?=?2;
4:?1,?4; m4?=?1;
5:?1,?4,?5; m5?=?1?+?|4?-?5|?=?2;
6:?1,?4,?6; m6?=?1?+?|4?-?6|?=?3;
7:?1,?4,?5,?7; m7?=?1?+?|4?-?5|?+?1?=?3.
题目很长，废话很多……
简单的说，n个城市排成一排，起点是第一个城市，每次可以向左或者右相邻城市走，路程为1
每个城市有一个捷径ai 表示第i个城市可以直接到ai城市，路程为1.
保证i <= ai <= a(i+1)
问从第一个城市出发，到达每个城市的最短路。
初级思路：dp 从做到右跑一遍 妥妥挂
5 5 5 5 5
dp: 0 1 2 3 1
ans: 0 1 2 2 1
中级思路：截半，走一个捷径后，从捷径开始，往前更新到当前位置和捷径之间的中点处 TLE
正解：bfs/spfa 单元最短路径啊啊啊啊啊！！！！！……
代码如下：
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <vector>
#define LL long long
#define Pr pair<int,int>
#define VI vector<int>
using namespace std;
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
int nt[233333];
int dp[233333];
bool vis[233333];
int n;
void bfs()
{
memset(dp,INF,sizeof(dp));
memset(vis,0,sizeof(vis));
dp[1] = 0;
vis[1] = 1;
queue <int> q;
q.push(1);
int u;
while(!q.empty())
{
u = q.front();
q.pop();
vis[u] = 0;
if(u+1 <= n && dp[u+1] > dp[u]+1)
{
dp[u+1] = dp[u]+1;
if(!vis[u+1])
{
vis[u+1] = 1;
<span style="white-space:pre"> </span>q.push(u+1);
}
}
if(u-1 > 0 && dp[u-1] > dp[u]+1)
{
dp[u-1] = dp[u]+1;
if(!vis[u-1])
{
vis[u-1] = 1;
<span style="white-space:pre"> </span>q.push(u-1);
}
}
if(dp[nt[u]] > dp[u]+1)
{
dp[nt[u]] = dp[u]+1;
if(!vis[nt[u]])
{
vis[nt[u]] = 1;
<span style="white-space:pre"> </span>q.push(nt[u]);
}
}
}
}
int main()
{
scanf("%d",&n);
for(int i = 1; i <= n; ++i)
scanf("%d",&nt[i]);
bfs();
for(int i = 1; i <= n; ++i)
{
if(i != 1) putchar(' ');
printf("%d",dp[i]);
}
return 0;
}Bad news came to Mike‘s village, some thieves stole a bunch of chocolates from the local factory! Horrible!
Aside from loving sweet things, thieves from this area are known to be very greedy. So after a thief takes his number of chocolates for himself, the next thief will take exactly k times more than the previous one. The value of k (k?>?1) is a secret integer known only to them. It is also known that each thief‘s bag can carry at most n chocolates (if they intend to take more, the deal is cancelled) and that there were exactly four thieves involved.
Sadly, only the thieves know the value of n, but rumours say that the numbers of ways they could have taken the chocolates (for a fixedn, but not fixed k) is m. Two ways are considered different if one of the thieves (they should be numbered in the order they take chocolates) took different number of chocolates in them.
Mike want to track the thieves down, so he wants to know what their bags are and value of n will help him in that. Please find the smallest possible value of n or tell him that the rumors are false and there is no such n.
The single line of input contains the integer m (1?≤?m?≤?1015) — the number of ways the thieves might steal the chocolates, as rumours say.
Print the only integer n — the maximum amount of chocolates that thieves‘ bags can carry. If there are more than one n satisfying the rumors, print the smallest one.
If there is no such n for a false-rumoured m, print ?-?1.
1
8
8
54
10
-1
In the first sample case the smallest n that leads to exactly one way of stealing chocolates is n?=?8, whereas the amounts of stealed chocolates are (1,?2,?4,?8) (the number of chocolates stolen by each of the thieves).
In the second sample case the smallest n that leads to exactly 8 ways is n?=?54 with the possibilities:(1,?2,?4,?8),??(1,?3,?9,?27),??(2,?4,?8,?16),??(2,?6,?18,?54),??(3,?6,?12,?24),??(4,?8,?16,?32),??(5,?10,?20,?40),??(6,?12,?24,?48).
There is no n leading to exactly 10 ways of stealing chocolates in the third sample case.
被坑边界了……
题目大意：四个小偷想偷巧克力。偷得方案符合如下规则：
巧克力无数，但小偷们的背包容量固定为n(每个小偷最多偷n块巧克力
第一个小偷随意拿，之后三个小偷按照签一个小偷的倍数拿，保证倍数一定。
譬如 1,2,4,8，第一个拿1块，之后每人拿前一人的二倍。 倍数>1
给出方案数目，问背包容量n为多少可以偷出这么多方案。
如果有多解，输出最少的背包容量。
细想一下，其实中间两个小偷无所谓。如果枚举第一个小偷偷的巧克力x的话。倍数为p，最后一个小偷其实偷了p*p*p*x*（<= n）
这样只要枚举所有背包容量n，每个容量枚举x，对于每个x枚举所有p即可得到总方案数。
没错，这样肯定TLE。
那么优化一下，当背包容量n递增时，其实方案数也是递增状态，同时要求的也是最小的n。单调函数，不就可以二分了么！
二分背包容量，搞出来方案数，跟m比较，然后继续二分。
至于方案数，刚才说枚举第一个小偷偷的巧克力数量，第二层枚举倍数。这样时间复杂度还是很恐怖。其实倒过来，枚举倍数的话，其实对于已知容量n，已知倍数x下。
能偷得方案数其实就是n/x 自然取整即可
挂就挂在二分范围上了。。。再开大点就好……当时测的时候测最大数据了。-1.然后就很单纯的以为应该是-1……
代码如下：
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <vector>
#define LL long long
#define Pr pair<int,int>
#define VI vector<int>
using namespace std;
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
LL cal(LL x, LL m)
{
LL tmp = 2;
LL cnt = 0;
while(1)
{
LL c = tmp*tmp*tmp;
if(c > x) return cnt;
cnt = cnt+x/c;
if(cnt > m) return cnt;
tmp++;
}
}
int main()
{
LL m;
scanf("%lld",&m);
LL l,r;
LL ans = -1;
l = 1,r =1e16;
while(l <= r)
{
LL mid = (l+r)/2;
LL tmp = cal(mid,m);
if(tmp >= m)
{
r = mid-1;
if(tmp == m) ans = mid;
}else l = mid+1;
}
printf("%lld\n",ans);
return 0;
}Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?
Every one of them has an integer sequences a and b of
length n. Being given a query of the form of pair of integers (l,?r),
Mike can instantly tell the value of 
while
!Mike can instantly tell the value of 
.
Now suppose a robot (you!) asks them all possible different queries of pairs of integers (l,?r) (1?≤?l?≤?r?≤?n) (so
he will make exactlyn(n?+?1)?/?2 queries) and counts how many times their answers coincide, thus for how many pairs 
is
satisfied.
How many occasions will the robot count?
The first line contains only integer n (1?≤?n?≤?200?000).
The second line contains n integer numbers a1,?a2,?...,?an (?-?109?≤?ai?≤?109) — the sequence a.
The third line contains n integer numbers b1,?b2,?...,?bn (?-?109?≤?bi?≤?109) — the sequence b.
Print the only integer number — the number of occasions the robot will count, thus for how many pairs is
satisfied.
6 1 2 3 2 1 4 6 7 1 2 3 2
2
3 3 3 3 1 1 1
0
The occasions in the first sample case are:
1.l?=?4,r?=?4 since max{2}?=?min{2}.
2.l?=?4,r?=?5 since max{2,?1}?=?min{2,?3}.
There are no occasions in the second sample case since Mike will answer 3 to any query pair, but !Mike will always answer 1.
RMQ+二分上下边界
没错，就是题面意思的RMQ。。当时做的时候不敢相信RMQ能搞出来，然后就在死扣一些旁门左道……
题目大意：给出两个长为n的序列a和b
问有多少个区间[L,R]满足max<a>[L,R] == min<b>[L,R]
感觉RMQ搞不出，死活往分治上搞……
其实明白做法后真的就是恍然大悟那种……然后深深哀怨自己脑子不够灵光=，=
RMQ二进制预处理还有查询就不说了 这个不知道就百度从RMQ开始补吧
然后就是枚举左边界L，因为对于a序列，L确定后，R从左到右走，最大值是单调不减的 对于序列b，最小值是单调不增的。
也就是两者都满足单调性。这样两者会有一段交集，就是a的最大值 == b的最小值。注意，这是一段R
在往左会出现max<a>[L,R] < min<b>[L,R] 再往右会出现max<a>[L,R] > min<b>[L,R]
这样就很有二分的味道了。
二分两次，第一次找到第一个相等的地方，第二次找到最后。这样对于当前的L，满足题意的区间个数就是两个位置之前的元素(右边界R)个数
不知道会不会爆int 反正我开了long long
代码如下：
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <vector>
#include <cmath>
#define LL long long
#define Pr pair<int,int>
#define VI vector<int>
using namespace std;
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
int rmq[2][20][200200];
void init(int n)
{
for(int i = 0; i < n; ++i)
scanf("%d",&rmq[0][0][i]);
for(int i = 0; i < n; ++i)
scanf("%d",&rmq[1][0][i]);
for(int k = 1; (1<<k) <= n; ++k)
for(int i = 0; i+(1<<k) <= n; ++i)
rmq[0][k][i] = max(rmq[0][k-1][i],rmq[0][k-1][i+(1<<(k-1))]);
for(int k = 1; (1<<k) <= n; ++k)
for(int i = 0; i+(1<<k) <= n; ++i)
rmq[1][k][i] = min(rmq[1][k-1][i],rmq[1][k-1][i+(1<<(k-1))]);
}
int Search(int pos,int l,int r)
{
int k = log((r-l+1)*1.0)/log(2.0);
if(pos) return min(rmq[pos][k][l],rmq[pos][k][r-(1<<k)+1]);
else return max(rmq[pos][k][l],rmq[pos][k][r-(1<<k)+1]);
}
int main()
{
int n;
scanf("%d",&n);
init(n);
// for(int i = 0; i < n; ++i)
// for(int j = i; j < n; ++j)
// printf("%d-%d max:%d min:%d\n",i,j,Search(0,i,j),Search(1,i,j));
LL ans = 0;
int l,r,st,en,a,b;
for(int i = 0; i < n; ++i)
{
l = i;
r = n-1;
st = -1;
while(l <= r)
{
int mid = (l+r)/2;
a = Search(0,i,mid);
b = Search(1,i,mid);
// printf("%d-%d max%d min%d\n",i,mid,a,b);
if(a >= b)
{
if(a == b) st = mid;
r = mid-1;
}
else l = mid+1;
}
if(st == -1) continue;
l = i;
r = n-1;
en = -1;
while(l <= r)
{
int mid = (l+r)/2;
a = Search(0,i,mid);
b = Search(1,i,mid);
// printf("%d-%d max%d min%d\n",i,mid,a,b);
if(a > b) r = mid-1;
else
{
en = mid;
l = mid+1;
}
}
// printf("%d: %d-%d\n",i,st,en);
ans += (en-st+1);
}
printf("%lld\n",ans);
return 0;
}
Mike wants to prepare for IMO but he doesn‘t know geometry, so his teacher gave him an interesting geometry problem. Let‘s definef([l,?r])?=?r?-?l?+?1 to
be the number of integer points in the segment [l,?r] with l?≤?r (say
that 
).
You are given two integers nand k and n closed
intervals [li,?ri] on OX axis
and you have to find:
In other words, you should find the sum of the number of integer points in the intersection of any k of the segments.
As the answer may be very large, output it modulo 1000000007 (109?+?7).
Mike can‘t solve this problem so he needs your help. You will help him, won‘t you?
The first line contains two integers n and k (1?≤?k?≤?n?≤?200?000) — the number of segments and the number of segments in intersection groups respectively.
Then n lines follow, the i-th line contains two integers li,?ri (?-?109?≤?li?≤?ri?≤?109), describing i-th segment bounds.
Print one integer number — the answer to Mike‘s problem modulo 1000000007 (109?+?7) in the only line.
3 2 1 2 1 3 2 3
5
3 3 1 3 1 3 1 3
3
3 1 1 2 2 3 3 4
6
In the first example:
;
;
.
So the answer is 2?+?1?+?2?=?5.
最后一直在扣这题，一直在往排序，然后优先队列那种做法上想。。。
题目大意是给出n个区间，从中取出k个区间，相交可以得到一个交集[L,R] 价值为R-L+1
问所有分法k个区间交集的价值和为多少
扫描线什么原理自行百度。。
这里一样的 存位置(L和R+1)和标记(1<左边界>或者-1<右边界>)
按位置排序。
这样从左到右扫，用一个cnt存扫到当前位置时，还有几个区间在。
用一个pre存放前一个位置
这样当前点位置为x
x-pre这段位置，其实被cnt个区间包含。
这样C(cnt,k)其实就是取到x-pre这一价值的分法个数
这一个先想明白，比较烧脑……
最后结果其实就是所有的C(cnt,k)*(x-pre)
至于C(cnt,k) 因为k比较大，并且题目中对大素数取模
因此可以用小费马预处理一下。
对于C(k,k)为1
C(k+1,k) = (k+1)！/k！*(k+1-k)！= C(k,k)*(k+1)/(k+1-k)
C(k+2,k) = (k+2)！/k！*(k+2-k)！= C(k+1,k)*(k+2)/(k+2-k)
发现了吧。这样O(n)地处理出来，除法用小费马转换为乘法即可。
代码如下：
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <vector>
#include <algorithm>
#define LL long long
#define Pr pair<int,int>
#define VI vector<int>
using namespace std;
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
const int mod = 1e9+7;
struct Node
{
int x,ad;
bool operator <(const struct Node a)const
{
return x == a.x? ad < a.ad: x < a.x;
}
};
Node nd[666666];
LL mult[666666];
int tp;
LL pow_m(LL a,int b)
{
LL ans = 1;
while(b)
{
if(b&1) ans = (ans*a)%mod;
b >>= 1;
a = (a*a)%mod;
}
return ans;
}
void init(int k,int n)
{
mult[k] = 1;
for(int i = k+1; i <= n; ++i)
{
mult[i] = ((mult[i-1]*i)%mod*pow_m(i-k,mod-2))%mod;
}
}
int main()
{
int n,k,l,r;
scanf("%d%d",&n,&k);
init(k,n);
tp = 0;
for(int i = 0; i < n; ++i)
{
scanf("%d%d",&l,&r);
nd[tp].x = l;
nd[tp++].ad = 1;
nd[tp].x = r+1;
nd[tp++].ad = -1;
}
sort(nd,nd+tp);
int cnt = 0,pre = 0;
LL ans = 0;
for(int i = 0; i < tp; ++i)
{
if(cnt >= k) ans = (ans+(nd[i].x-pre)*mult[cnt])%mod;
cnt += nd[i].ad;
pre = nd[i].x;
}
printf("%lld\n",ans);
return 0;
}【CF】Codeforces Round #361 (Div. 2)
标签：
原文地址：http://blog.csdn.net/challengerrumble/article/details/51866796
