[ACM] POJ 2593 Max Sequence (动态规划,最大字段和）

标签：acm   动态规划   

Description

Give you N integers a1, a2 ... aN (|ai| <=1000, 1 <= i <= N). 

You should output S. 

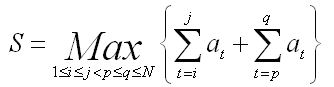
Input

Output

Sample Input

5
-5 9 -5 11 20
0

Sample Output

40

Source

同 POJ 2479http://blog.csdn.net/sr_19930829/article/details/38397435

题意要求为给定一个数字序列，找出两段不相交的子段，使这两个子段的和最大，求出这个最大值。

dp[i]表示 从位置1到i 之间的最大子段和，正向求一遍。然后逆向求最大子段和，比如逆向求出当前位置i的最大字段和为sum,那么 ans= max( ans,dp[i-1]+sum)， ans即为答案。

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
const int maxn=100010;
const int inf=-0x7fffffff;
int dp[maxn];
int num[maxn];
int t,n;

void DP()//正向求最大子段和
{
    memset(dp,0,sizeof(dp));
    int sum=inf,b=inf;
    for(int i=1;i<=n;i++)
    {
        if(b>0)
            b+=num[i];
        else
            b=num[i];
        if(b>sum)
        {
            sum=b;
            dp[i]=sum;
        }
    }
}

int main()
{
    while(scanf("%d",&n)!=EOF&&n)
    {
        for(int i=1;i<=n;i++)
            scanf("%d",&num[i]);
        DP();
        int ans=inf,b=0,sum=inf;//逆向求n到i最大字段和，与正向的最大字段和相加，求出最大值
        for(int i=n;i>1;i--)
        {
            if(b>0)
                b+=num[i];
            else
                b=num[i];
            if(b>sum)
                sum=b;
            if(sum+dp[i-1]>ans)
                ans=sum+dp[i-1];
        }
        printf("%d\n",ans);
    }
    return 0;
}

[ACM] POJ 2593 Max Sequence (动态规划,最大字段和）,布布扣,bubuko.com

[ACM] POJ 2593 Max Sequence (动态规划,最大字段和）

标签：acm   动态规划   

原文地址：http://blog.csdn.net/sr_19930829/article/details/38397597