标签:
例说信号处理与滤波器设计
许多公式在转换时成了乱码,相应的word版本请点这里
目录
信号处理是对原始信号进行改变,以提取有用信息的过程,它是对信号进行变换、滤波、分析、综合等处理过程的统称。数字信号处理是将信号以数字方式表示并处理的理论和技术;模拟信号处理是指用模拟系统对模拟信号进行处理的方法或过程。
数字信号处理课程的主要内容包括信号分析与处理。两者并不是孤立的,不同的信号处理方法往往需要选择不同的信号表示形式。两者的区别主要表现在,信号处理是用系统改变输入信号,以得到所期望的输出信号,如信号去噪;而信号分析往往是通过变换(傅里叶变换、小波变换等),或其它手段提取信号的某些特征,如语音信号的基本频率,图像的直方图等。
早期的信号处理局限于模拟信号,随着数字计算机的飞速发展,信号处理的理论和方法得以飞速发展,出现了不受物理制约的纯数学的加工,即算法,并确立了数字信号处理的领域。现在,对于信号的处理,人们通常是先把模拟信号变成数字信号,然后利用高效的数字信号处理器(DSP:Digital Signal Processor)或计算机对其进行数字形式的信号处理。
一般地讲,数字信号处理涉及三个步骤:

图 1数字信号处理基本步骤

图 2家庭影院(视+听)
高分辨率图像、高保真音质

图 3语音识别
噪声环境下高识别率

图 4图像增强
更清晰、美观

图 5无人驾驶
高度智能、安全
图 6医学成像
更高效、更精确的成像结果
狭义地讲,信号处理可以统称为滤波,根据不同的要求,选用不同性能的滤波器。在数字信号处理应用中,设计合适的滤波器至关重要。什么是数字滤波器呢?数字滤波器就是数字信号处理(Digital Signal Processing)算法,或者是数字信号处理器件(Digital Signal Processor)。什么是数字信号处理算法呢?我们需要借助基本的数学工具和方法。
首先回到信号处理的根本目的:用滤波器改变输入信号,以期得到理想的输出信号,如果输入信号用$x\left[ n \right]$表示,输出信号用$y\left[ n \right]$表示,则数字信号处理或滤波可用如下框图表示:

图 7数字信号滤波图示
上述框图并没有给出数字信号处理算法的具体实现方法,但提供了数字信号处理的基本数学思想:通过系统将$x\left[ n \right]$和$y\left[ n \right]$进行关联。在数学上描述$x$和$y$之间关系的手段有很多,如函数$y = f\left( x \right)$,方程组\[Ax = y\]等,从数学角度来理解,如果$f\left( \cdot \right)$为不同映射,即使同样的自变量$x$,也会得到不同的因变量$y$;如果系数矩阵\[A\]不同,同样的\[x\]经变换之后,将得到不同的\[y\]。在数字信号处理课程中,描述输入输出信号关系的基本数学工具是差分方程:
\[\sum\limits_{k = 0}^Q {{a_k}y\left[ {n - k} \right]} = \sum\limits_{k = 0}^P {{b_k}x\left[ {n - k} \right]} \]
令$N = \max \left( {P,Q} \right)$,上述差分方程可写为
\[\sum\limits_{k = 0}^N {{a_k}y\left[ {n - k} \right]} = \sum\limits_{k = 0}^N {{b_k}x\left[ {n - k} \right]} \]
如果仅局限于基础(经典)的数字信号处理算法研究,全部内容都是围绕这个常系数线性差分方程(Constant Coefficient Linear Difference Equation,CCLDE)展开的。那么,我们需要研究CCLDE什么呢?很显然,我们可以将CCLDE看成一个系统,它描述了输入$x\left[ n \right]$和输出$y\left[ n \right]$之间的关系。哪些参数决定这个系统的性能呢?方程中除了$x\left[ n \right]$和$y\left[ n \right]$,还有三个参数:方程阶数$N$,系数${a_k}$和${b_k}$——数字滤波器设计的根本任务就是确定这三个参数——目标非常明确!!!
从何下手呢?如何判定所设计的滤波器符合预期呢?迷茫中ing…
烈日当空,窗外的知了热得撕心裂肺地吼叫

声音特点:又大又尖,怎叫人不心烦意乱?!
大:能量大,或者信号幅度大(声压级超过120dB即达到痛阈);
尖:频率高,即知了的叫声中包含了丰富的高频成分,因此听起来很"刺耳"。
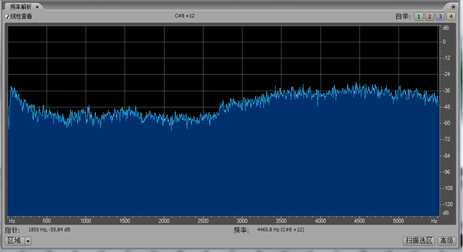
图 8知了声的频谱图(横坐标:频率(Hz);纵坐标:幅度(dB))
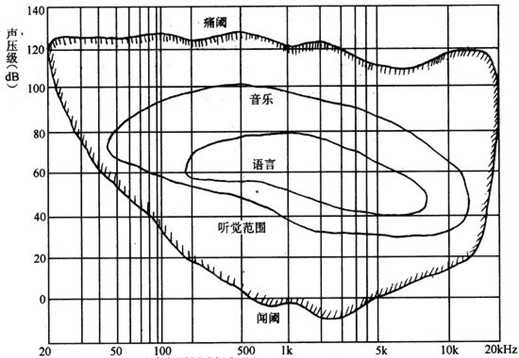
图 9 听觉曲线
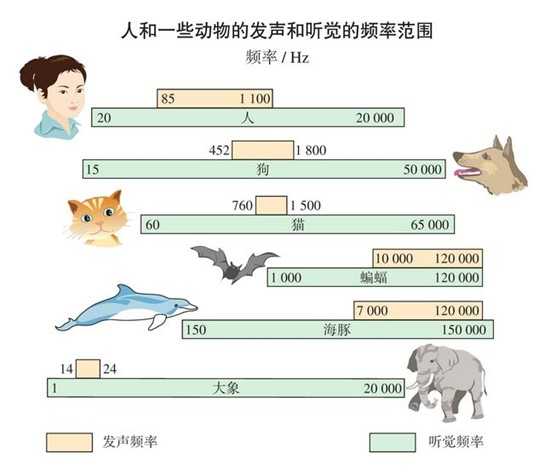
图 10 声音频率范围
可见,幅度和频率是声音信号的主要参数。诸如"低音炮"、"高音喇叭"、"男低音"和"女高音"都是从幅度和频率去描述声音信号的,因此,分析信号的频率特性是信号处理领域的重要内容。
分析信号的频率特性无非就是想知道信号包含了哪些频率成分,各频率成分的大小是多少。傅里叶分析完美地解决了这个问题。在信号与系统课程中,我们通常将傅里叶分析分为傅里叶级数和傅里叶变换,前者用来对付周期信号,后者用来处理非周期信号,但无论是傅里叶级数,还是傅里叶变换(当然,傅里叶级数也可以纳入到傅里叶变换体系中),它们的原理或宗旨都一样:将一般的信号分解为基本信号的线性组合
(连续周期信号) \[\tilde x\left( t \right) = \sum\limits_{k = - \infty }^{ + \infty } {{a_k}{e^{jk{\omega _0}t}}} \]
(离散非周期序列) \[x\left[ n \right] = \frac{1}{{2\pi }}\int_{\left\langle {2\pi } \right\rangle } {X\left( {{e^{j\omega }}} \right)} {e^{j\omega n}}d\omega \]
以式为例,等式左边是一般的(满足收敛条件的)周期信号,而右边则是频率为$k{\omega _0}$、幅度为${a_k}$的虚指数信号\[{e^{jk{\omega _0}t}}\]的线性组合。
现在可以谈论一下滤波的概念了。假设式中\[\tilde x\left( t \right)\]就是知了发出的"嗞哇嗞哇……"没完没了的周期信号,现在我们想把烦人的高频成分去掉,最直观的想法就是需要设计一个滤波器,这个滤波器可以让较低频率的信号顺利通过,同时又能阻止较高频率的信号,这就是所谓的低通滤波器。
再回到常系数线性差分方程,参数$N$,${a_k}$和${b_k}$完全决定了方程所描述的系统的所有特性。什么?难道与输入$x\left[ n \right]$和输出$y\left[ n \right]$没关系?对,没有关系!电阻是一个系统,其阻值仅与自身的材料及结构有关,虽然有关系式$R = v\left( t \right)/i\left( t \right)$,事实上,即使两端没有电压,电阻依然存在;再比如理想的线性放大电器,它的增益仅取决于内部结构,而与输入输出无关,但为了测量放大器的增益(放大倍数),我们可以在输入端接入幅度为$i$的信号,然后测量输出信号的幅度$o$,这样就可以得到放大倍数$g = \frac{o}{i}$,更特殊地,如果取$i = 1$,此时输出信号的幅度就是放大器的增益,即$g = o$。类似的概念推广到CCLDE描述的LTI系统,我们如何获得这个系统的特性呢?输入——输出描述法,即令输入$x\left[ n \right]$取某种特殊值时,计算(或测量)系统的输出$y\left[ n \right]$。那么,什么样的$x\left[ n \right]$算特殊呢?单位脉冲!
\[\delta \left[ n \right] = \left\{ \begin{array}{l}
1,\;\;\;n = 0\\
0,\;\;n \ne 0
\end{array} \right.\]
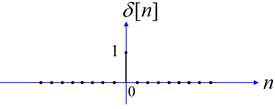
也就是说,令$x\left[ n \right] = \delta \left[ n \right]$,此时系统的输出就是所谓的单位脉冲响应$h\left[ n \right]$。再与放大器的例子对比一下:输入信号幅度$i = 1$,输出信号的幅度$o$就是放大倍数(放大器的重要指标,从应用者角度而言,其实就是唯一关心的指标)。我们有理由相信,对于CCLDE描述的LTI系统,得到了单位脉冲响应$h\left[ n \right]$,就能够掌握系统的全部特性(因果性、稳定性、频率选择性等)。何以见得呢?之后将逐步解答。
现在,我们假设已经知道了LTI系统的单位脉冲响应$h\left[ n \right]$,对于任意输入$x\left[ n \right]$,如何求系统的输出$y\left[ n \right]$呢?其实就是求滤波后的信号。首先,我们要建立已知和需求之间的联系。已知的是 ,需求是
,需求是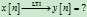 。
。
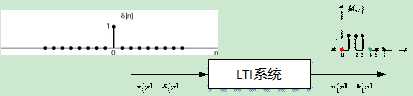
图 11 单位脉冲响应
事实上,任意序列$x\left[ n \right]$很容易用$\delta \left[ n \right]$的移位、加权的线性组合来表示:$x\left[ n \right] = \sum\limits_{k = - \infty }^{ + \infty } {x\left[ k \right]\delta \left[ {n - k} \right]} $。
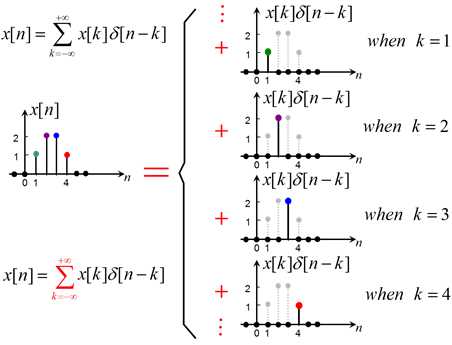
图 12 序列的单位脉冲表示
结合系统的线性和时不变性,有
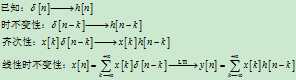
式中最后一个等式\[y\left[ n \right] = \sum\limits_{k = - \infty }^{ + \infty } {x\left[ k \right]h\left[ {n - k} \right]} \]就是卷积和,记作$y\left[ n \right] = x\left[ n \right]*h\left[ n \right]$,表明LTI系统的(零状态)响应$y\left[ n \right]$是单位脉冲响应$h\left[ n \right]$的移位、加权、求和。这句话也描述了求$y\left[ n \right]$的步骤。根据图 4,我们可以假想有这样的一个LTI系统——出钞机:如果你今天往出钞机投币口(输入端)投币一元,它将在接下来的三天,每一天都会从出币口(输出端)吐出一元。试问:如果某个月的1、3、4日,你分别投了2、2、3元,那么,出钞机每天的输出是多少元呢?不妨用图来说明一下。
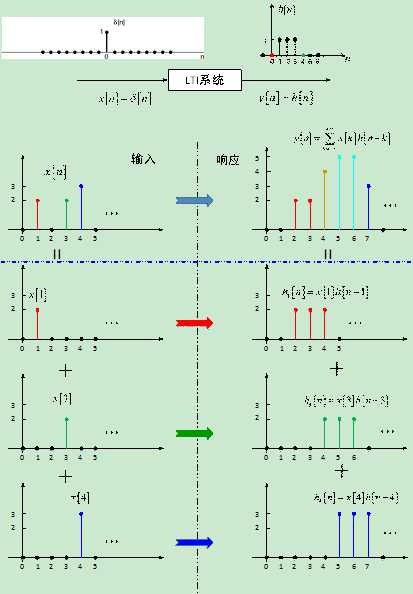
图 13 卷积和的图解
图解结果告诉我们,出钞机在2-7日分别吐出2,2,4,5,5,3元。图解的过程包含了乘积与求和("积"与"和"),但并有体现出"卷"(翻转)这一操作。如果只想求某一天(比如5日)出钞口吐出多少钱,此时就要用另一种方法,即许多教材中描述的步骤:
以上步骤包含了"卷积和"所有的操作(卷——翻转;积——相乘;和——相加)。
图解过程是根据线性时不变系统的定义导出的一种结果,是系统特性的直接反映。卷积和是信号与系统、数字信号处理中最重要的公式之一,它描述了LTI系统输入$x\left[ n \right]$、输出$y\left[ n \right]$以及单位脉冲响应$h\left[ n \right]$之间的关系,已知三者中的任何两个,就可以确定第三者,于是就有以下应用场合:
现在,我们将注意力集中到卷积和公式上来,公式重写如下
\[y\left[ n \right] = \sum\limits_{k = - \infty }^{ + \infty } {x\left[ k \right]h\left[ {n - k} \right]} \]
卷积和只包含了移位、数乘和相加运算,看来,数字信号处理的计算十分简单。如果再上升一个层次,卷积和能很直观解释系统如何改变输入信号的吗?从图 6的结果很难看出系统是如何将$x\left[ n \right]$变成$y\left[ n \right]$的,而且也很难说明这种变化意味着什么,因此,卷积和在解释系统行为特性时很不直观,这是卷积和运算本身决定的。
了解运算背后的物理或几何含义对理解问题的本质至关重要。例如向量的乘法和加法:设两个向量\[\vec A = {x_1} + i{y_1}\],\[\vec B = {x_2} + i{y_2}\],向量的加法符合平行四边形法则,从图 7很容易看出两个向量相加的几何意义,而相应的代数运算也很简单——对应分量相加即可,即有
\[\vec C = \vec A + \vec B = \left( {{x_1} + {x_2}} \right) + i\left( {{y_1} + {y_2}} \right)\]
但如果要求两个向量的乘法呢?代数运算的结果是
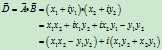
相比两个向量的加法,向量的乘法运算要复杂一些,更重要的是,根据运算结果,我们很难看清向量乘法的几何意义。如果将向量$\vec A$和$\vec B$用极坐标表示,情况又会如何呢?设
\[\begin{array}{l}
\vec A = \left( {{\rho _1},{\theta _1}} \right) = {\rho _1}{e^{j{\theta _1}}}\\
\vec B = \left( {{\rho _2},{\theta _2}} \right) = {\rho _2}{e^{j{\theta _2}}}
\end{array}\]
则两个向量的乘法

计算简单,几何意义明确——模相乘,相位相加。
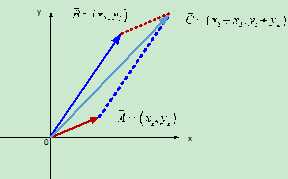
图 14 向量加的直角坐标表示
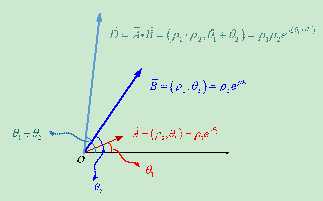
图 15 向量乘法的极坐标表示
向量运算的例子告诉我们,选择不同的坐标系,不仅影响运算的复杂度,在解释运算的几何意义时也各有千秋。上例告诉我们,如果是向量的加法,直角坐标系比极坐标系方便;如果是向量的乘法,很显然,极坐标系比直角坐标系方便。
回到数字信号处理的话题,卷积和是让无数人困惑的公式,然而,它又是经典数字信号处理算法的根源。既然卷积和运算就是滤波,我们如何评判滤波的效果呢?从什么角度理解系统的滤波行为更好呢?
再想想知了的叫声,之所以烦人,是因为包含了大量的高频分量。看来,用频率这一参数来解释信号特性很符合人的直观感觉。我们有更好的方式来洞悉卷积和的物理意义吗?能不能站在频(率)域的角度来解释卷积和呢?当然可以,因为我们有卷积定理(性质):
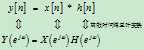
通过傅里叶变换,将时域中的卷积和运算换成了频域中的相乘运算。那么频域中的相乘运算有什么好处呢?不要忘了,我们主要是为了直观解释滤波的行为和特性。
图 9是一段滤波前知了声$x\left[ n \right]$的时域波形,单从图形上看,似乎很难说出这一段信号的特点,运用傅里叶变换,得到$x\left[ n \right]$的幅度谱\[\left| {X\left( {{e^{j\omega }}} \right)} \right|\]如图 10所示,很明显,该图说明信号$x\left[ n \right]$包含了丰富的高频成分。现在,我们希望设计一个滤波器,可以滤除2500Hz以上的频率分量,目的是仅保留红框内的频率分量,因此要求滤波器的频率响应(幅频响应)是
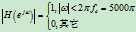
滤波器的幅频特性如图 11所示,截止频率${f_c} = 2500$Hz。由卷积定理可知,输出信号的幅度谱为
\[\left| {Y\left( {{e^{j\omega }}} \right)} \right| = \left| {X\left( {{e^{j\omega }}} \right)} \right|\left| {H\left( {{e^{j\omega }}} \right)} \right|\]
从图形上来看就更直观了:图 10与图 11相乘,得到了滤波后信号的幅度谱,滤波前、后信号频谱的变化一目了然,很显然,它是按照滤波器频率响应\[H\left( {{e^{j\omega }}} \right)\]所规定的形状去改变的。而对比滤波前、后的时域波形,很难解释信号的什么特性被改变了。
在上述的讨论中,我们只关注幅度谱,实际中,相位谱也必须考虑,更完整的表达式为
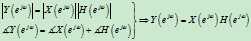
对比极坐标系下两个向量的乘法,能找到相似之处吗?——模相乘、相位相加。如果将卷积和$y\left[ n \right] = x\left[ n \right]*h\left[ n \right]$看作直角坐标系下两个向量的乘法,那么\[Y\left( {{e^{j\omega }}} \right) = X\left( {{e^{j\omega }}} \right)H\left( {{e^{j\omega }}} \right)\]就类似于极坐标系下两个向量的乘法——运算简单、物理意义直观。[通过向量乘法运算的例子,我们可以看到,向量的表示方式起到了关键性的作用;同样地,信号也有不同的描述方式,如时域、频域、复频域,不同的表示方法都是为了使分析问题更简单、物理意义更明确]
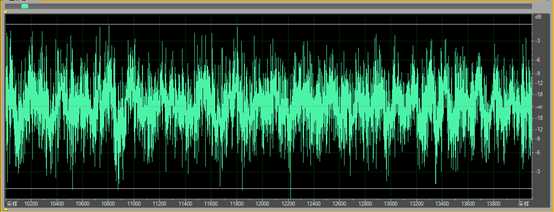
图 16滤波前知了声$x\left[ n \right]$时域波形
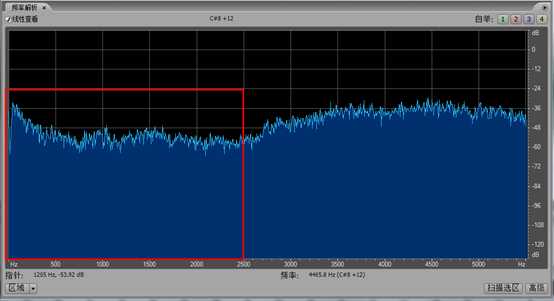
图 17滤波前知了声的幅度谱\[\left| {X\left( {{e^{j\omega }}} \right)} \right|\] (红框是希望保留的低频分量)
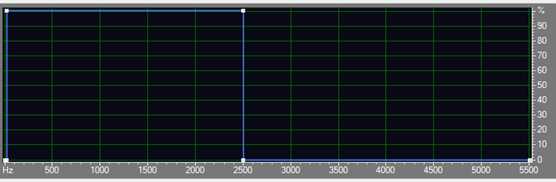
图 18低通滤波器幅频特性\[\left| {H\left( {{e^{j\omega }}} \right)} \right|\] (蓝色线)
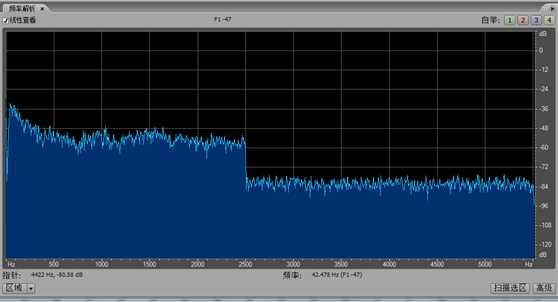
图 19滤波后知了声的幅度谱\[\left| {Y\left( {{e^{j\omega }}} \right)} \right|\]
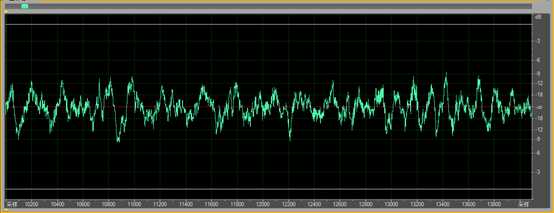
图 20滤波后知了声$y\left[ n \right]$时域波形
借助系统的频率响应\[H\left( {{e^{j\omega }}} \right)\],可以很方便地解释滤波器的特性(主要是指频率选择性)。有什么定量指标来描述频率选择性吗?通常有四个指标——横坐标两个,纵坐标两个。以低通滤波器为例来说明。如图 14所示,横坐标两个指标为通带截止频率\[{\omega _p}\]和阻带截止频率\[{\omega _s}\],纵坐标两个指标为通带衰减\[{A_p}\]和阻带衰减\[{A_s}\]。
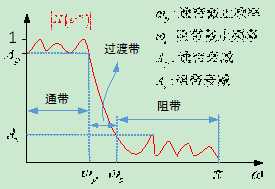
图 21数字低通滤波器指标
通常而言,滤波器设计就是指根据应用的需求,提出合理的滤波器指标(通带截止频率和衰减,阻带截止频率和衰减),然后借助滤波器设计工具得到滤波器参数(系数)。滤波器系数?没听说过啊,是什么东西?其实我们早见过面了,就是差分方程中的${a_k}$和${b_k}$!早就说过,数字滤波器设计要不忘初心,根本任务就是确定这三个参数——方程的阶数$N$,系数${a_k}$和${b_k}$。
如何建立起滤波器指标和滤波器系数之间的联系呢?很显然,滤波器的指标约束着其频率响应\[H\left( {{e^{j\omega }}} \right)\],而\[H\left( {{e^{j\omega }}} \right)\]与CCLDE的阶数$N$,系数${a_k}$和${b_k}$直接相关。傅里叶变换又该出场了。对差分方程两边取傅里叶变换得
\[\sum\limits_{k = 0}^N {{a_k}{e^{ - jk\omega }}Y\left( {{e^{j\omega }}} \right)} = \sum\limits_{k = 0}^N {{b_k}{e^{ - jk\omega }}X\left( {{e^{j\omega }}} \right)} \]
从而可得频率响应
\[H\left( {{e^{j\omega }}} \right) = \frac{{Y\left( {{e^{j\omega }}} \right)}}{{X\left( {{e^{j\omega }}} \right)}} = \frac{{\sum\limits_{k = 0}^N {{b_k}{e^{ - jk\omega }}} }}{{\sum\limits_{k = 0}^N {{a_k}{e^{ - jk\omega }}} }}\]
易见,频率响应\[H\left( {{e^{j\omega }}} \right)\]完全由$N$,${a_k}$和${b_k}$确定。综上可知,滤波器设计就是如何根据滤波器指标求解滤波器系数的过程,从数学角度来看,就是函数逼近和数值优化的过程。经典滤波器设计理论发展较完备(巴特沃斯、切比雪夫I、切比雪夫II、椭圆……,各自的特点是什么?更多内容,请点这里),许多教科书都有详细讨论,此处不再赘述,我们的重点是要借助现代化的设计工具,轻松完成设计任务并实施滤波处理。此处仅以MATLAB工具为例,并通过两种方式来实现滤波器设计——脚本代码和可视化方法。
需求:设计一个低通滤波器来处理知了声,通带截止频率\[{F_p} = 2000\]Hz,通带衰减${A_p} = 0.1$dB,阻带截止频率\[{F_s} = 2500\]Hz,通带衰减${A_p} = 50$dB。
乍一看,这些指标与图 14中的指标完全不同,实际需求的指标往往同本例,频率指标为模拟频率,衰减指标以dB为单位,而设计数字滤波器时,往往需要数字频率指标。如何进行指标转换呢?直接用公式计算${\omega _p} = 2\pi {F_p} = 4000\pi $,${\omega _s} = 2\pi {F_s} = 5000\pi $吗?图 14告诉我们,无论通带截止频率,还是阻带截止频率都不会超过$\pi $。难道最大的数字角频率就是$\pi $吗?为什么?这个问题同样令许多人困惑。如何衡量数字频率的大小呢?先考虑一个简单的数字信号:$x\left[ n \right] = \cos \left( {\omega n} \right)$,针对$\omega $取不同的值,分别画出对应的波形如下:
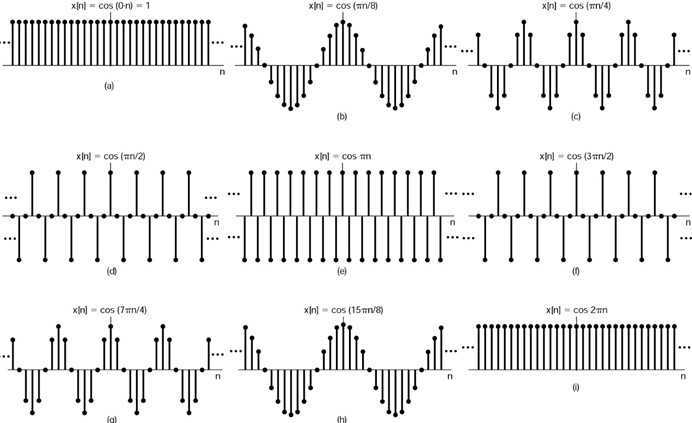
图 22$\cos \left( {\omega n} \right)$波形图
振荡得越厉害,意味着频率越高,这是符合常理的。上图中的9个波形,哪个振荡得最厉害呢?第二排中间那个——+1和-1交替,而此时$\omega = \pi $。而且还发现,$\omega = 0$和$\omega = 2\pi $的波形一样,并不是$\omega $的值越大,振荡得越快。如果是连续时间信号$x\left( t \right) = \cos \left( {2\pi ft} \right) = \cos \left( {\Omega t} \right)$,大家都知道,随着$\Omega $的增大,波形会振荡得越快。从连续时间信号到离散时间信号,是什么原因导致两者出现如此大的差异呢?通过对采样过程的探索,我们便可理解其中的奥妙。设以时间间隔${T_s}$对$x\left( t \right) = \cos \left( {\Omega t} \right)$采样,这样便得到
$x\left( {n{T_s}} \right) = \cos \left( {\Omega n{T_s}} \right) = \cos \left( {\omega n} \right)$
因此有
$\omega = \Omega {T_s} = \Omega /{f_s}$
其中\[{f_s} = 1/{T_s}\]为采样频率,$\Omega $为模拟角频率,$\omega $为数字角频率。结论是:数字频率是模拟频率关于采样频率的归一化。
根据Nyquist采样定理,当采样频率大于信号最高频率2倍时,可以由样点完全恢复原来的信号。我们不妨假设信号的最高频率正好是采样频率的一半,即\[{f_{\max }} = {f_s}/2\],对应的最高模拟角频率${\Omega _{\max }} = 2\pi {f_{\max }} = \pi {f_s}$,代入式得
${\omega _{\max }} = {\Omega _{\max }}/{f_s} = \pi {f_s}/{f_s} = \pi $
这也证明了为什么最高数字角频率为$\pi $。(如果不满足Nyquist采样条件又会怎样呢?事实上并不影响结论成立)。关于各种频率之间的关系的讨论,可以参考这里(注意文中"fdtool工具中归一化频率为什么最大只到0.5的原因",应改为"最大只到1的原因"。)
再回到滤波器设计题目,第一步,需要将模拟频率指标转换为归一化数字频率指标,转换公式是
\[\omega = 2f/{f_s}\;\;\;\;(\pi )\]
很显然,我们需要知道采样频率${f_s}$。知了声的采样频率${f_s} = 11025$Hz。将模拟频率指标代入式计算出对应的归一化数字频率指标
\[\begin{array}{l}
{\omega _p} = 2{F_p}/{f_s} = 2 \times 2000/11025 \approx 0.36\\
{\omega _s} = 2{F_s}/{f_s} = 2 \times 2500/11025 \approx 0.45
\end{array}\]
这样,我们就得到了数字域的四个指标:${\omega _p},{A_p},{\omega _s},{A_s}$。如何从这四个指标去计算滤波器系数呢?有现成的公式套用,即许多教科书上所说的各类滤波器原型。我们选择椭圆型滤波器为例。MATLAB代码如下:
clc;
close all
fs=11025; %采样频率(Hz)
Fp = 2000; %通带截止频率(Hz)
Fs = 2500; %阻带截止频率(Hz)
Ap = 0.1; %通带衰减(dB)
As = 50; %阻带衰减(dB)
wp=2*Fp/fs; %归一化通带截止频率
ws=2*Fs/fs; %归一化阻带截止频率
[N,Wp]=ellipord(wp,ws,Ap,As); %确定带通滤波器的阶数和截止频率
[b,a]=ellip(N,Ap,As,Wp); %确定滤波器系数
[h,w]=freqz(b,a); %求数字带通滤波器的频率响应
%以下为绘图命令,绘制带通滤波器的幅频响应
figure;
plot(w*fs/(2*pi),20*log10(abs(h)/max(abs(h))));
axis([0,fs/2,-100,0]);
title(‘数字低通滤波器的幅度响应‘);
xlabel(‘频率(Hz)‘);
ylabel(‘幅度(dB)‘);
grid
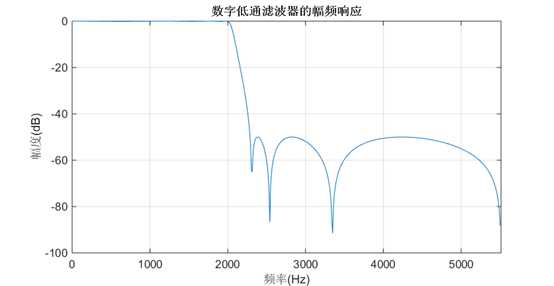
滤波器系数
a = [1 -2.98876196757509 5.41154092244290 -6.18465137960809 4.94650037623018 -2.65349822687766 0.903727225595414 -0.150115115698030]
b = [0.0204237714181223 0.0185281305134523 0.0518202070683316 0.0515988082549051 0.0515988082549052 0.0518202070683315 0.0185281305134523 0.0204237714181222]
分别对应式中的${a_k}$和${b_k}$,得到了这两个参数,滤波器设计基本上算完成了。
如果你掌握了滤波器设计的基本理论,但又不想写代码,你可以利用FDATool轻松完成滤波器设计的全过程。
在命令窗口输入:fdatool,回车,就可以看到下图所示的界面:
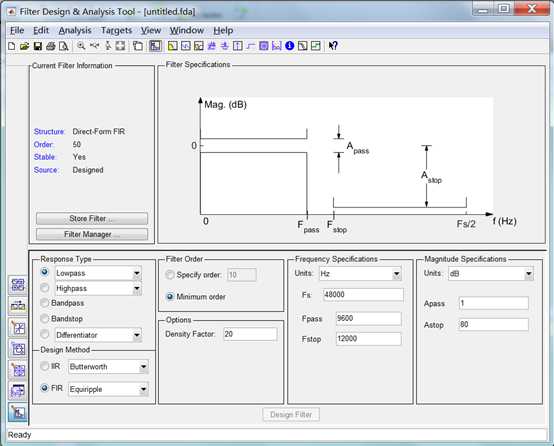
然后动动鼠标就可以完成滤波器设计了。针对本例,我们按下图红框所示设定指标,在完成指标设定之后,点"Design Filter"按钮即完成设计。关于滤波器的所有信息,都可以通过菜单或工具栏获得。注意"Current Filter Information"部分,它描述了当前所设计出的滤波器基本信息,包括结构、阶次、稳定性等。有一个问题值得思考:滤波器的结构对滤波器的工程实现有什么影响呢?成本、稳定性、抗噪声性能,这些都与结构有关,因此,掌握滤波器各种结构的优缺点也十分重要。
很显然,用FDATool设计滤波器十分简单!无论采用什么方法,都不要忘记滤波器设计的根本目标——得到滤波器系数。关于FDATool更多内容,请点这里和这里。
当滤波器设计完成之后,我们该考虑如何用所得到的系数对输入信号进行滤波了。
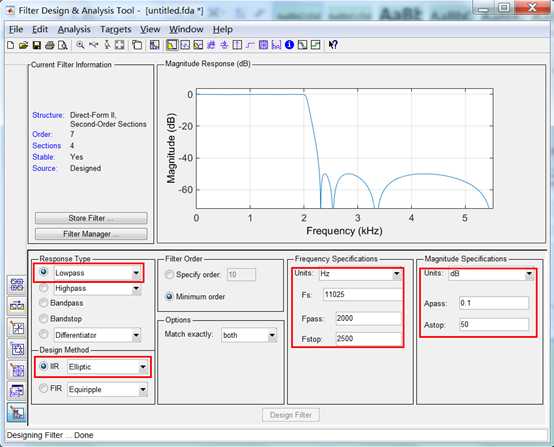
当滤波器系数${a_k}$和${b_k}$确定之后,方程也就完全确定了,所谓的滤波,就是要对给定的输入$x\left[ n \right]$,求系统的响应$y\left[ n \right]$。MATLAB提供了几种滤波实现函数:
conv:线性卷积,可以用来实现滤波
filter:滤波,但是输出点数和输入点数相同,其余的存在内部状态中,以便处理后续输入
filtfilt:零相位滤波,输出通过滤波器后再反向通过滤波器,消除相位影响
fftfilt:利用基于FFT的重叠相加法对数据进行滤波,这种频域滤波技术只对FIR滤波器有效
完整例子:用MATLAB读入知了声的音频文件,画时域波形和频谱,设计滤波器,对音频文件进行滤波,最后画滤波后的信号时域波形和频谱。程序如下:
clc;
close all
[xn, fs] = wavread(‘cicada.wav‘); %读wav文件(知了声),获得样点值xn和采样频率fs
%计算信号xn的频谱
xn_FFT = fft(xn); %FFT频谱分析
xn_FFT_AMP = abs(xn_FFT); %求xn的幅度谱
xn_FFT_AMP_db = 20*log10(xn_FFT_AMP/max(xn_FFT_AMP)); %用对数表示
%画xn时域波形
figure
n = 1:length(xn); %生成样点横坐标向量
plot(n,xn); %以n为横坐标,画xn
axis([1 length(xn) -1 1]) %设定坐标轴显示范围
xlabel(‘样点‘); %设定x坐标标记
ylabel(‘幅度‘); %设定y坐标标记
title(‘知了声时域波形‘); %设定标题
%画xn的幅度谱(对数形式)
figure
faxis = (0:length(xn)-1)*fs/length(xn); %生成横坐标(频率轴)刻度,FFT的频率范围[0 fs]
plot(faxis,xn_FFT_AMP_db); %以faxis为横轴画xn频谱图
axis([0 fs/2 -100 0]) %设定显示范围,由于FFT频谱具有对称性,因此只显示前半部分
xlabel(‘频率(Hz)‘);
ylabel(‘幅度(dB)‘);
title(‘知了声幅度谱‘);
% 设计低通滤波器
Fp = 2000; %通带截止频率(Hz)
Fs = 2500; %阻带截止频率(Hz)
Ap = 0.1; %通带衰减(dB)
As = 50; %阻带衰减(dB)
wp=2*Fp/fs; %归一化通带截止频率
ws=2*Fs/fs; %归一化阻带截止频率
[N,Wp]=ellipord(wp,ws,Ap,As); %确定带通滤波器的阶数和边缘频率
[b,a]=ellip(N,Ap,As,Wp); %确定滤波器系数
[h,w]=freqz(b,a); %求数字带通滤波器的频率响应
%以下为绘图命令,绘制带通滤波器的幅频响应
figure;
plot(w*fs/(2*pi),20*log10(abs(h)/max(abs(h))));
axis([0,fs/2,-100,0]);
title(‘数字低通滤波器的幅度响应‘);
xlabel(‘频率(Hz)‘);
ylabel(‘幅度(dB)‘);
grid
%利用设计的滤波器对xn进行滤波,得到滤波输出yn
yn = filter(b,a,xn); %滤波函数,b和a为滤波器系数,xn是输入信号
wavwrite(yn,fs,8,‘cicada_LPFiltered.wav‘); %保存滤波后的信号
%画滤波后的信号yn时域波形
figure
n = 1:length(yn);
plot(n,yn);
axis([1 length(yn) -1 1])
xlabel(‘样点‘);
ylabel(‘幅度‘);
title(‘低通滤波后知了声时域波形‘);
%计算滤波后信号yn的频谱
yn_FFT = fft(yn);
yn_FFT_AMP = abs(yn_FFT);
yn_FFT_AMP_db = 20*log10(yn_FFT_AMP/max(yn_FFT_AMP));
figure
faxis = (0:length(yn)-1)*fs/length(yn);
plot(faxis,yn_FFT_AMP_db);
axis([0 fs/2 -100 0])
xlabel(‘频率(Hz)‘);
ylabel(‘幅度(dB)‘);
title(‘滤波后知了声幅度谱‘);
结果:
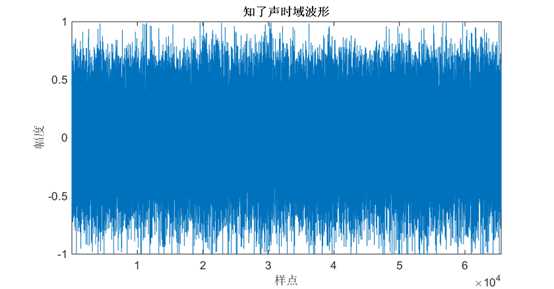
图 23知了声时域波形
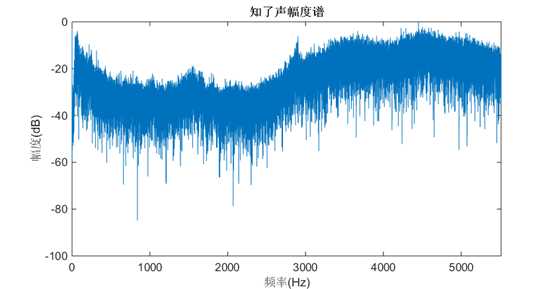
图 24知了声频谱(幅度频)
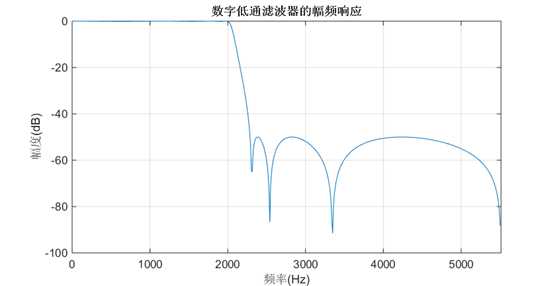
图 25低通滤波器频率响应(幅频响应)
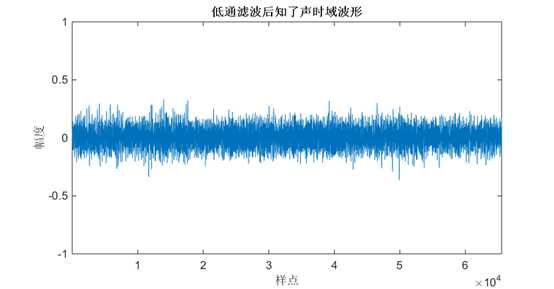
图 26低通滤波后知了声时域波形
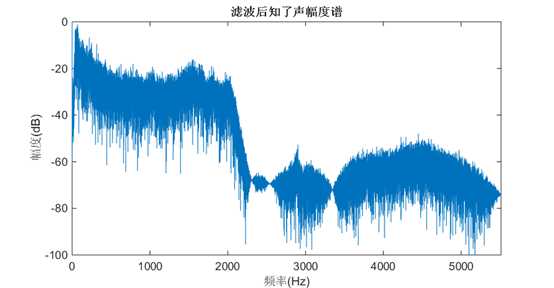
图 27滤波后知了声频谱图(幅度谱)
经典信号处理课程的主要内容:
欢迎加入数字信号处理群:152346662
标签:
原文地址:http://www.cnblogs.com/gemstoneatxm/p/5659569.html