标签:
作者:白宁超
2016年7月12日14:28:10
摘要:最早接触马尔可夫模型的定义源于吴军先生《数学之美》一书,起初觉得深奥难懂且无什么用场。直到学习自然语言处理时,才真正使用到隐马尔可夫模型,并体会到此模型的妙用之处。马尔可夫模型在处理序列分类时具体强大的功能,诸如解决:词类标注、语音识别、句子切分、字素音位转换、局部句法剖析、语块分析、命名实体识别、信息抽取等。另外广泛应用于自然科学、工程技术、生物科技、公用事业、信道编码等多个领域。本文写作思路如下:第一篇对马尔可夫个人简介和马尔科夫链的介绍;第二篇介绍马尔可夫链(显马尔可夫模型)和隐马尔可夫模型以及隐马尔可夫模型的三大问题(似然度、编码、参数学习);第三至五篇逐一介绍三大问题相关算法:(向前算法、维特比算法、向前向后算法);最后非常得益于冯志伟先生自然语言处理教程一书,冯老研究自然语言几十余载,在此领域别有建树。(本文原创,转载注明出处:向前向后算法解决隐马尔可夫模型机器学习问题 )
【自然语言处理:马尔可夫模型(一)】:初识马尔可夫和马尔可夫链
【自然语言处理:马尔可夫模型(二)】:马尔可夫模型与隐马尔可夫模型
【自然语言处理:马尔可夫模型(三)】:向前算法解决隐马尔可夫模型似然度问题
【自然语言处理:马尔可夫模型(四)】:维特比算法解决隐马尔可夫模型解码问题(中文句法标注)
【自然语言处理:马尔可夫模型(五)】:向前向后算法解决隐马尔可夫模型机器学习问题
安德烈·马尔可夫,俄罗斯人,物理-数学博士,圣彼得堡科学院院士,彼得堡数学学派的代表人物,以数论和概率论方面的工作著称,他的主要著作有《概率演算》等。1878年,荣获金质奖章,1905年被授予功勋教授称号。马尔可夫是彼得堡数学学派的代表人物。以数论和概率论方面的工作著称。他的主要著作有《概率演算》等。在数论方面,他研究了连分数和二次不定式理论 ,解决了许多难题 。在概率论中,他发展了矩阵法,扩大了大数律和中心极限定理的应用范围。马尔可夫最重要的工作是在1906~1912年间,提出并研究了一种能用数学分析方法研究自然过程的一般图式——马尔可夫链。同时开创了对一种无后效性的随机过程——马尔可夫过程的研究。马尔可夫经多次观察试验发现,一个系统的状态转换过程中第n次转换获得的状态常取决于前一次(第(n-1)次)试验的结果。马尔可夫进行深入研究后指出:对于一个系统,由一个状态转至另一个状态的转换过程中,存在着转移概率,并且这种转移概率可以依据其紧接的前一种状态推算出来,与该系统的原始状态和此次转移前的马尔可夫过程无关。马尔可夫链理论与方法在现代已经被广泛应用于自然科学、工程技术和公用事业中。
向前向后算法解决:问题3(学习问题):给定一个观察序列O和一个HMM中的状态集合,自动学习HMM的参数A和B。
此算法涉及机器学习,较为复杂,笔者不打算深入讲解,感兴趣的同学可以参考冯志伟《自然语言处理简明教程》P594—602,本文只是做为了解方面讲解。
鲍姆-韦尔奇算法(Baum-Welch algorithm):训练HMM的标准算法是向前向后算法,这是期望最大化算法或者叫鲍姆-韦尔奇算法,这个算法帮助我们训练HMM的转移概率B和发射概率A。
鲍姆-韦尔奇算法思路:
(1) 反复的估计所得的计数,从转移概率和观察概率的一个估计值开始,反复的使用这些估计概率来推出越来越好的概率。
(2) 对于一个观察,计算它向前概率,从而得到我们估计的概率。然后把这个估计的概率量,在对于这个向前概率有贡献的所有不同路径上进行分摊。
向后概率:向后概率记住 β是对于给定自动机 λ,在状态i和时刻t观察下一个时刻t+1到终点的观察概率,用公式表示如下:
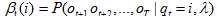
计算向前概率相似的归纳法来计算向后概率:

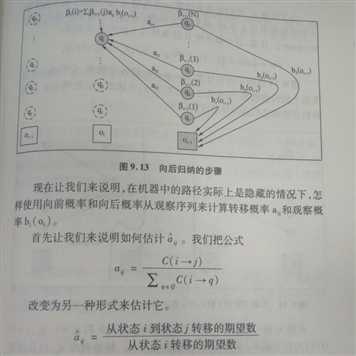



【1】统计自然语言处理基础 Christopher.Manning等 著 宛春法等 译
【2】自然语言处理简明教程 冯志伟 著
【3】数学之美 吴军 著
【4】Viterbi算法分析文章 王亚强
声明:关于此文各个篇章,本人采取梳理扼要,顺畅通明的写作手法。一则参照相关资料二则根据自己理解进行梳理。避免冗杂不清,每篇文章读者可理清核心知识,再找相关文献系统阅读。另外,要学会举一反三,不要死盯着定义或者某个例子不放。诸如:此文章例子冰淇淋数量(观察值)与天气冷热(隐藏值)例子,读者不免问道此有何用?我们将冰淇淋数量换成中文文本或者语音(观察序列),将天气冷热换成英文文本或者语音文字(隐藏序列)。把这个问题解决了不就是解决了文本翻译、语音识别、自然语言理解等等。解决了自然语言的识别和理解,再应用到现在机器人或者其他设备中,不就达到实用和联系现实生活的目的了?本文原创,转载注明出处:向前向后算法解决隐马尔可夫模型机器学习问题
标签:
原文地址:http://www.cnblogs.com/baiboy/p/hmm5.html