标签:
在连续随机变量这部分,有一种特殊的随机变量X,对于X所有可能取值,P(X)都相等,我们称其为均匀随机变量。
基于均匀随机变量的定义,我们容易看到,其密度函数f(x)必然是一条平行于x轴的直线,因为这样才能够保证如下等式成立。
对于X∈[a,b]的随机变量,我们能够直接得到其密度函数是f(x)=1/(b-a),x∈[a,b].
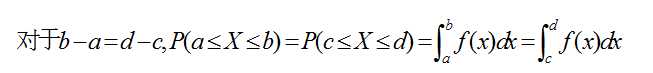
下面我们来看一个均匀随机变量的例子。
Q:向一个圆当中随机取一条弦,这条弦比该圆内接正三角形的边长要长的概率是多少?
分析:这其实是1889年法国数学家贝特朗提出的贝特朗悖论。
按照一般解决概率问题的策略,我们首相应该给出样本空间。
法一:样本空间Ω1={x|x为弦到圆心的距离}
法二:样本空间Ω2={x|x过弦端点的切线和弦围成的角度}
容易看到,对于不同的样本空间的定义方法,最终得到的结果是不同的。对于法一是1/2,对于法二的概率是1/3。
《A First Course in Probability》-chaper4-连续型随机变量-均匀随机变量
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5664157.html