标签:
大根堆的定义:1 大根堆是一个大根树 2 大根堆是一个完全二叉树
所以大根堆用数组表示是连续的,不会出现空白字段。
对于大根堆的插入
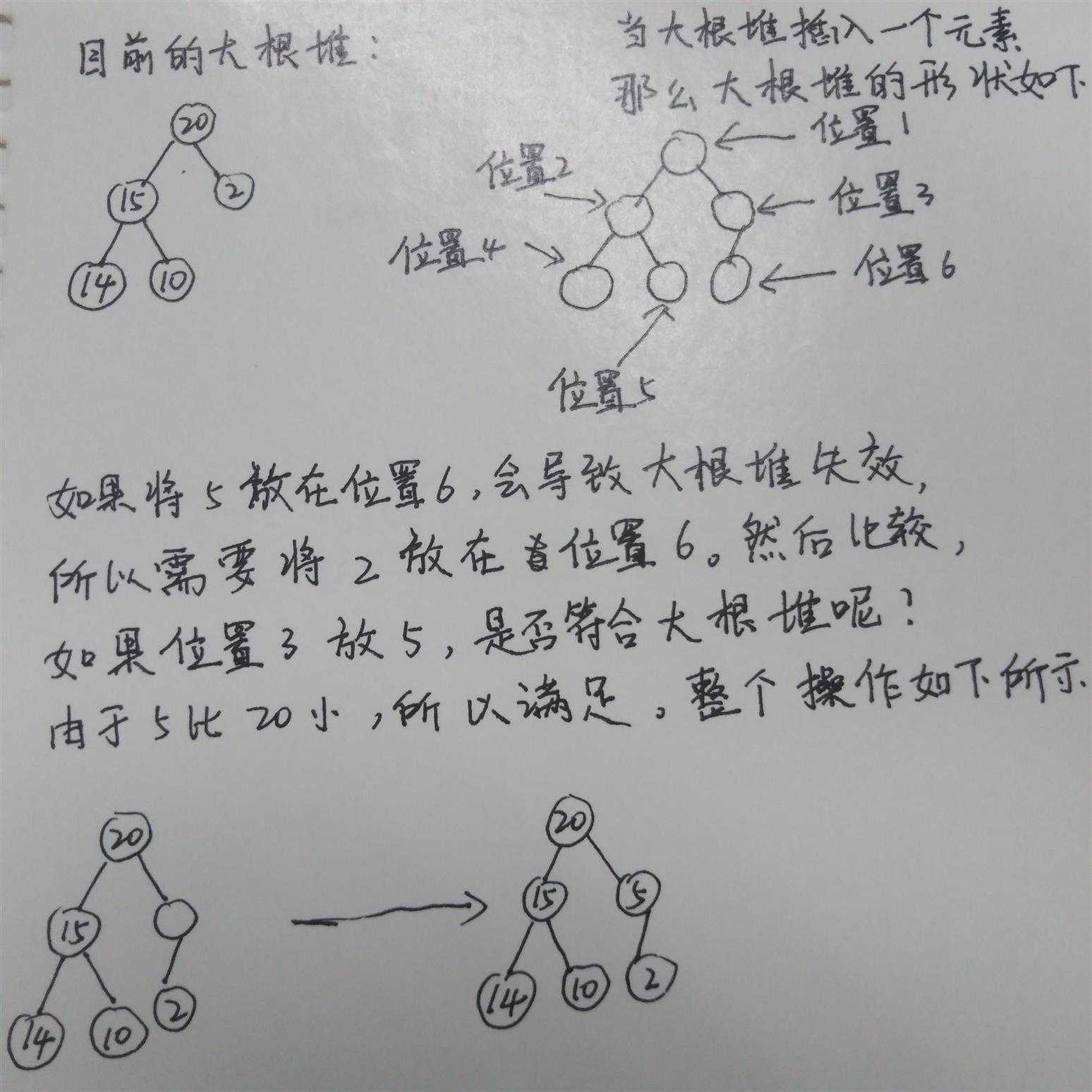
对于大根堆的插入,可以在排序前确定大根堆的形状,可以确定元素5从位置6插入,那么比较元素5和位置3的元素2,
元素5比元素2大,将2下移。接着比较元素5和元素20,一次类推,直到找到元素5的合理位置。
接着看一下如果插入的元素是21,怎么进行排序。
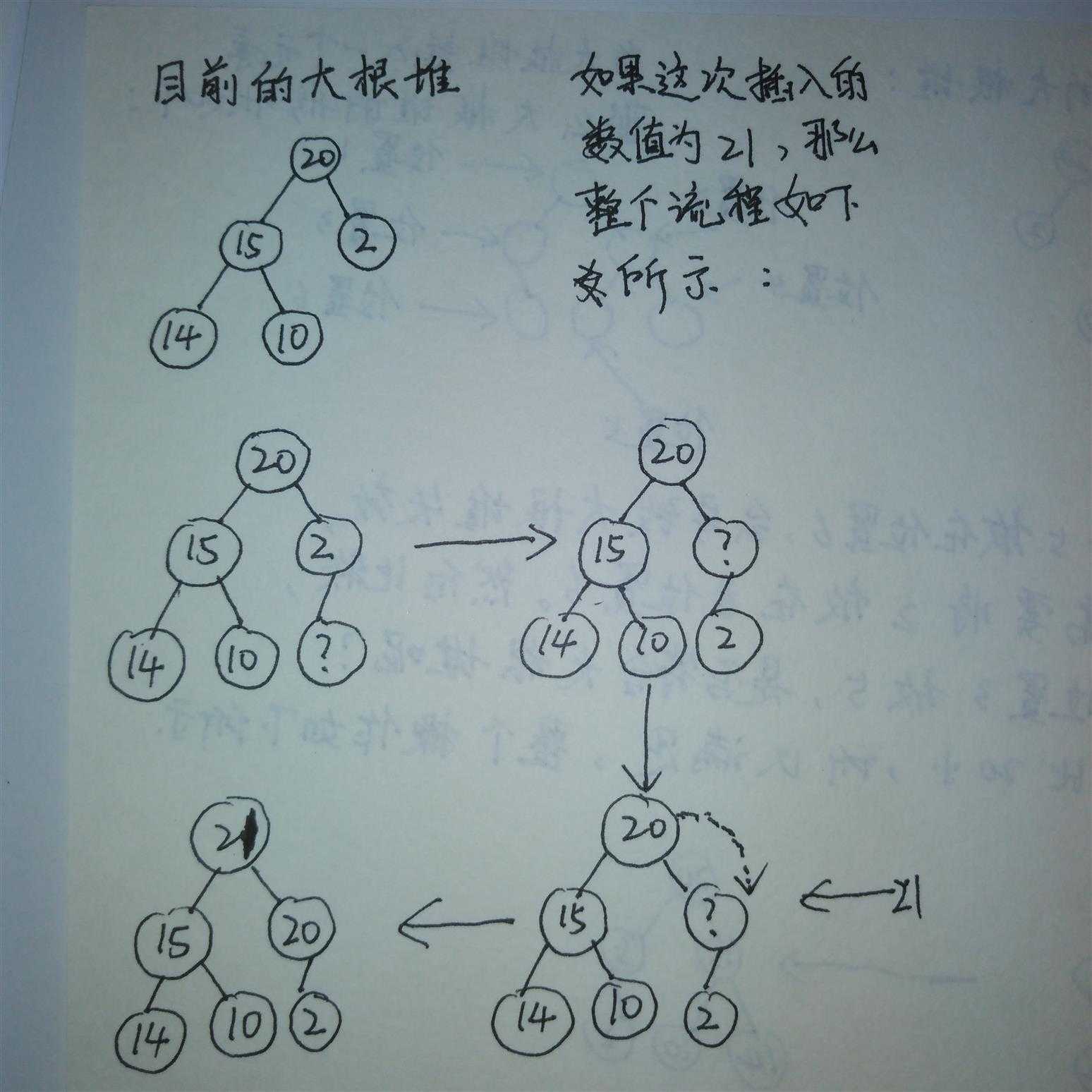
21比2大,所以将2下移,接着比较21和20,发现20比21小,20下移,最终21放到
根的位置。形成大根堆。
对于大根堆的删除
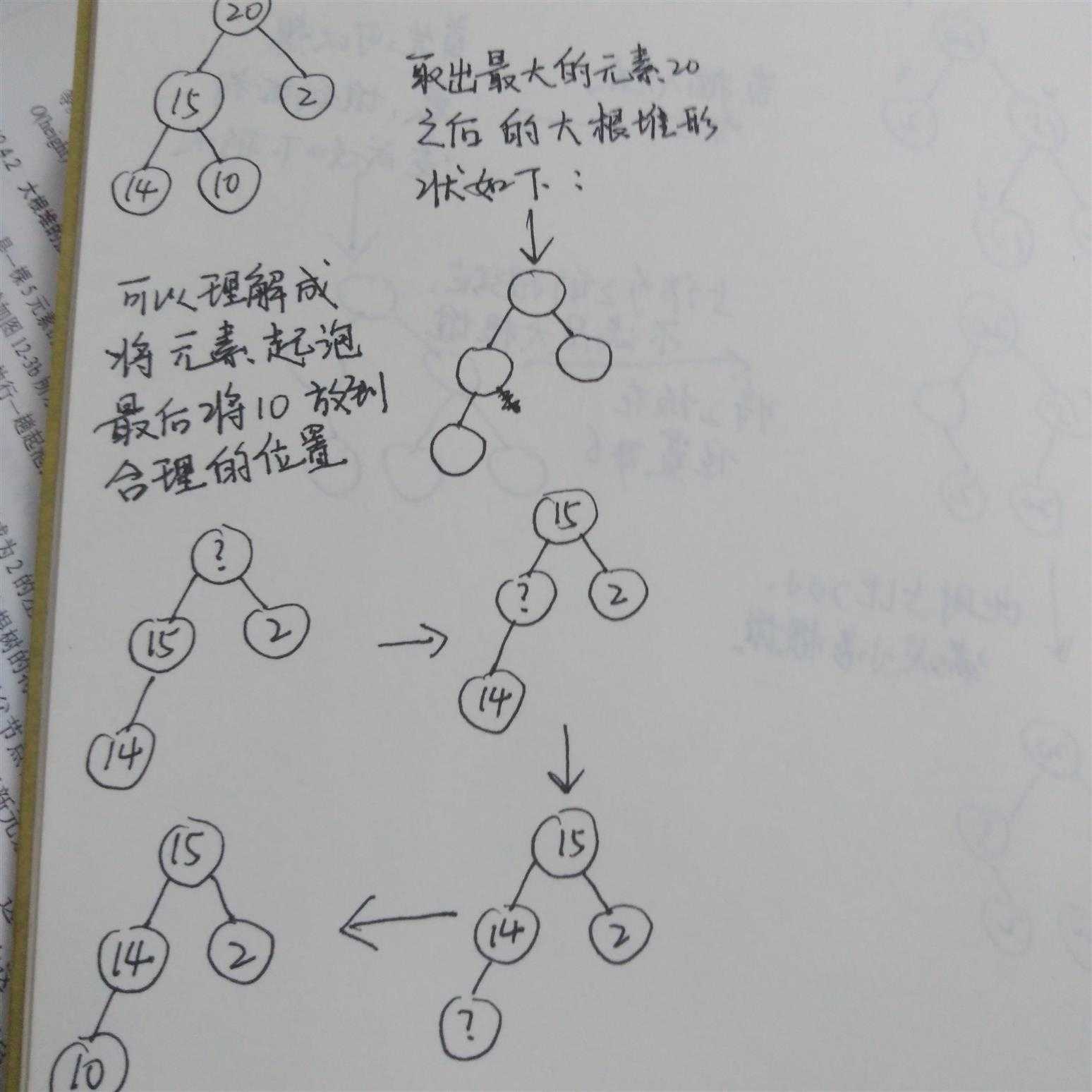
大根堆删除根元素,那么可以确定删除后的形状。可以理解成将最后一个叶子节点放在
合理位置,首先比较叶子节点元素10和根节点的两个孩子15和2,选出两个节点中最大的
元素15,15比10大,所以15进行气泡。放到根节点。然后15所在的位置2,变为不确定的问号。
由于14比10大,那么14起泡放到位置2,根据大根堆的形状,最后将10放到左节点。
将一个无序的完全二叉树变为大根堆

将一个无序的完全二叉树变为大根堆(或者小根堆),首先要找到最有一个叶子节点的父节点,
对该父节点为根节点的子树进行排序,生成一个大根堆(小根堆)。然后从节点位置依次
向前做同样的排序,将该节点到根节点的所有子树变为大根堆(小根堆)
举例子:

如上图所示,因为总共有6个节点,6/2 = 3,所以元素19的父节点是位置3的元素4,
将以4位根的子树变为大根堆。因为19比4大,所以19上移,4做叶子节点。依次类推,
从位置3到位置1的所有子树都按照这种逻辑处理,最终变成大根堆。
接着要处理位置2的子树,位置2的元素为1,两个节点为25和12,选最大的元素25,因为
25比1大,所以25进行上移,1变为叶子节点。这样位置2的子树就处理完了。
接着处理位置1,因为位置1的元素为6,两个节点分别为25和19,取最大节点元素25,
因为25比6大,所以25上移,而此时位置2还有两个节点元素1和元素12,需要比较元素6
和这两个节点中最大的,以确定大根堆。由于12比6大,所以12上移,6变为叶子节点。
最终用数组表示这个大根堆就是[25,12,19,1,6,4]
下面是代码实现和测试:
大根堆的类结构:
template <class T> class maxHeap { public: maxHeap(void) { m_nHeapSize = 0; m_nHeapCapacity = 0; m_pHeapArray = NULL; } maxHeap(const maxHeap& tempHeap); maxHeap(T * heapArray, int arrayLen); ~maxHeap(){ if(m_pHeapArray) { free(m_pHeapArray); } m_pHeapArray = NULL; m_nHeapSize = 0; m_nHeapCapacity = 0; } //插入节点 void insertNode(const T& t); //pop堆顶元素 const T& popRoot(); //打印自己的堆元素,用数组表示法输出 void printHeap(); //将一个无序的数组变为大根堆 void createMaxHeap(T * heapArray, int arrayLen); //销毁自己的堆元素 void deallocMaxHeap(); //打印数组的元素 void printHeap(T * heapArray, int arrayLen); private: //堆的数组元素,连续区间首地址 T* m_pHeapArray; //当前使用的大小 int m_nHeapSize; //堆的容量,实际开辟的大小 int m_nHeapCapacity; };
两个构造函数:
template <class T> maxHeap<T>::maxHeap(const maxHeap &tempHeap){ m_nHeapSize = tempHeap.m_nHeapSize; m_pHeapArray = malloc(sizeof(class maxHeap) *m_nHeapSize); m_nHeapCapacity = m_nHeapSize; } template <class T> maxHeap<T>::maxHeap(T * heapArray, int arrayLen) { m_nHeapSize = arrayLen; m_pHeapArray = malloc(sizeof(class maxHeap) * m_nHeapSize); m_nHeapCapacity = arrayLen; }
插入节点:
template <class T> void maxHeap<T>::insertNode(const T& node) { m_nHeapSize ++; if(m_nHeapSize >= m_nHeapCapacity) { m_pHeapArray = (T *)realloc(m_pHeapArray, sizeof(T) * m_nHeapSize *2); } m_nHeapCapacity = m_nHeapSize*2; //当前节点所在位置 int currentIndex = m_nHeapSize; //该节点父节点所在位置 int parentIndex = currentIndex/2; //当前节点为根节点,跳出循环直接插入即可 while(currentIndex != 1) { //父节点元素小于该node,因为是大根堆,所以父节点下移 if(m_pHeapArray[parentIndex -1] < node) { //父节点数据下移 m_pHeapArray[currentIndex - 1] = m_pHeapArray[parentIndex -1]; //更新当前节点位置,当前比较位置上移 currentIndex = currentIndex/2; //父节点位置同样上移 parentIndex = parentIndex/2; } else { break; } } //因为节点数是从1开始的,所以节点数-1表示数组中的位置 m_pHeapArray[currentIndex -1] = node; }
打印元素:
template <class T> void maxHeap<T>::printHeap() { cout <<"current max heap array is :" << endl; for(int i = 0; i < m_nHeapSize; i++) { cout << m_pHeapArray[i] << " "; } cout << endl; } template <class T> void maxHeap<T>::printHeap(T * heapArray, int arrayLen) { cout <<"current max heap array is :" << endl; for(int i = 0; i < arrayLen; i++) { cout << heapArray[i] << " "; } cout << endl; }
pop堆顶的元素,取出最大值
template <class T> const T& maxHeap<T>::popRoot() { //先取出最后的叶子节点 const T& lastEle = m_pHeapArray[m_nHeapSize-1]; //更新heapsize m_nHeapSize --; //删除时需要从根节点开始,找到最大值起泡 int currentIndex= 1; //当前节点的做孩子 int leftChild = currentIndex *2; //当前节点的孩子节点超过堆大小,说明该节点为叶子节点 while(leftChild <= m_nHeapSize) { int bigChild = leftChild; //取出两个孩子中大的孩子,然后将大的孩子节点数据上移 if(leftChild < m_nHeapSize && m_pHeapArray[leftChild-1] < m_pHeapArray[leftChild]) { //更新大孩子节点为右节点 bigChild = leftChild +1; } //比较两个节点中大的孩子节点和取出的最后叶子节点,那个数值大 //如果最后的叶子节点数值大,那么可以跳出循环,因为找到了lastEle的合理位置 //剩余的树也是大根堆 if(m_pHeapArray[bigChild -1] <= lastEle) { break; } //大节点数据上移 m_pHeapArray[currentIndex -1] = m_pHeapArray[bigChild-1]; //更新插入位置为当前大节点位置 currentIndex = bigChild; leftChild = currentIndex *2; } m_pHeapArray[currentIndex-1] = lastEle; return lastEle; }
将一个无序的数组元素,变为大根堆
template <class T> void maxHeap<T>::createMaxHeap(T * heapArray, int arrayLen) { //判断异常 if(arrayLen <= 0 || heapArray == NULL) { return ; } //从最后一个叶子节点的父节点开始,依次从该位置到根节点 //例如该位置为3,那么位置3,位置2,位置1的根节点的子树依次处理为大根堆 int currentIndex = arrayLen; //父节点位置 int beginIndex = currentIndex/2; //依次处理,形成子树大根堆 for(int i = beginIndex; i > 0; i--) { int rootEle = heapArray[i-1]; int curNode = i; int leftChild = i *2; while(leftChild <= arrayLen) { int bigChild = leftChild; int rootElePrint = heapArray[leftChild-1]; int rightElePrint = heapArray[leftChild+1 -1] ; if(leftChild +1 <= arrayLen && heapArray[leftChild+1 -1] > heapArray[leftChild-1]) { bigChild = leftChild +1; } if(heapArray[bigChild -1] <= rootEle ) { break; } heapArray[curNode -1] = heapArray[bigChild -1]; curNode = bigChild; leftChild = curNode *2; } heapArray[curNode -1] = rootEle; } }
源代码下载地址: http://download.csdn.net/detail/secondtonone1/9575112
整个代码就到这里吧,这是我的公众号,希望关注下:

标签:
原文地址:http://www.cnblogs.com/secondtonone1/p/5663047.html