标签：
The GCD table G of size n × n for an array of positive integers a of length n is defined by formula
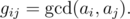
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as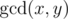 
. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
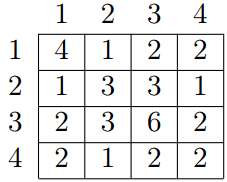
Given all the numbers of the GCD table G, restore array a.
The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.
All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.
In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.
4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
4 3 6 2
1
42
42
2
1 1 1 1
1 1
一眼就看出出现奇数次的一定是答案，然后yy了一下，觉得出现两次以上的偶数次的也是答案，五分钟出了这题，结果就fst了（出题人用心险恶，好吧其实是我太弱）。
正解应该是显然知道最大的数一定在答案中，每次引入答案中的数一定会和之前答案中有的数产生两个新的gcd值，划去原来数组中的这两个值，到最后就会留下答案了。
#include<iostream> #include<cstdio> #include<queue> #include<map> #include<algorithm> using namespace std; #define maxn 620 int a[maxn * maxn]; map<int, int> mp; int main() { int n; while(~scanf("%d", &n)) { for(int i = 1; i <= n * n; i++){ scanf("%d", &a[i]); mp[a[i]]++; } sort(a + 1, a + 1 + n * n); int cnt = 0; int ans[maxn]; for(int i = n * n; i >= 1; i--) { if(!mp[a[i]]) continue; mp[a[i]] --; for(int j = 1; j <= cnt; j++) { mp[__gcd(a[i], ans[j])] -= 2; } ans[++cnt] = a[i]; } for(int i = 1; i <= cnt; i++) printf("%d ", ans[i]); puts(""); } }
Codeforces Round #323 (Div. 2) C. GCD Table
标签：
原文地址：http://www.cnblogs.com/lonewanderer/p/5668213.html
