标签:
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2604
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4428 Accepted Submission(s): 1961

用f(n)表示n个人满足条件的结果,那么如果最后一个人是m的话,那么前n-1个满足条件即可,就是f(n-1);
如果最后一个是f那么这个还无法推出结果,那么往前再考虑一位:那么后三位可能是:mmf, fmf, mff, fff,其中fff和fmf不满足题意所以我们不考虑,但是如果是
mmf的话那么前n-3可以找满足条件的即:f(n-3);如果是mff的话,再往前考虑一位的话只有mmff满足条件即:f(n-4)
所以f(n)=f(n-1)+f(n-3)+f(n-4),递推会跪,可用矩阵快速幂
构造一个矩阵。
用f(n)表示n个人满足条件的结果,那么如果最后一个人是m的话,那么前n-1个满足条件即可,就是f(n-1);
如果最后一个是f那么这个还无法推出结果,那么往前再考虑一位:那么后三位可能是:mmf, fmf, mff, fff,其中fff和fmf不满足题意所以我们不考虑,但是如果是
mmf的话那么前n-3可以找满足条件的即:f(n-3);如果是mff的话,再往前考虑一位的话只有mmff满足条件即:f(n-4)
所以f(n)=f(n-1)+f(n-3)+f(n-4),递推会跪,可用矩阵快速幂
构造一个矩阵: 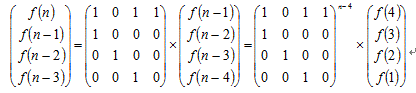
1 //快速幂矩阵 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 struct Mat 7 { 8 int mat[4][4]; 9 }; 10 int m; 11 Mat operator *(Mat a, Mat b) 12 { 13 Mat c; 14 memset(c.mat,0,sizeof(c.mat)); 15 int i, j, k; 16 //这儿的顺序按照 17 for(i = 0; i < 4; i++) 18 for(j = 0; j < 4; j++) 19 for(k = 0; k < 4; k++) 20 c.mat[i][j] = (c.mat[i][j] + a.mat[i][k]*b.mat[k][j])%m; 21 return c; 22 } 23 Mat multi(int n)//计算一个已知矩阵的n次方%m 24 { 25 Mat ans; 26 for(int i = 0; i < 4; i++) 27 { 28 for(int j = 0; j < 4; j++) 29 { 30 if(i==j) 31 ans.mat[i][j] = 1; 32 else ans.mat[i][j] = 0; 33 } 34 35 } 36 Mat a; 37 memset(a.mat,0,sizeof(a.mat)); 38 a.mat[0][0] = a.mat[0][2] = a.mat[0][3] = a.mat[1][0] = a.mat[2][1] = a.mat[3][2] = 1; 39 40 while(n>0) 41 { 42 if(n&1) ans = ans*a; 43 a = a*a; 44 n>>=1; 45 } 46 return ans; 47 } 48 int main() 49 { 50 int n; 51 while(~scanf("%d%d",&n,&m)) 52 { 53 if(n==1) printf("%d\n",2%m); 54 else if(n==2) printf("%d\n",4%m); 55 else if(n==3) printf("%d\n",6%m); 56 else if(n==4) printf("%d\n",9%m); 57 else 58 { 59 Mat t; 60 t = multi(n-4); 61 int sol = ((t.mat[0][0]*9)%m+(t.mat[0][1]*6)%m+(t.mat[0][2]*4)%m+(t.mat[0][3]*2)%m)%m; 62 printf("%d\n",sol); 63 } 64 } 65 return 0; 66 }
标签:
原文地址:http://www.cnblogs.com/shanyr/p/5668983.html