LSTM

In a traditional recurrent neural network, during the gradient back-propagation phase, the gradient signal can end up being multiplied a large number of times (as many as the number of timesteps) by the weight matrix associated with the connections between the neurons of the recurrent hidden layer. This means that, the magnitude of weights in the transition matrix can have a strong impact on the learning process.

If the weights in this matrix are small (or, more formally, if the leading eigenvalue of the weight matrix is smaller than 1.0), it can lead to a situation calledvanishing gradients where the gradient signal gets so small that learning either becomes very slow or stops working altogether. It can also make more difficult the task of learning long-term dependencies in the data. Conversely, if the weights in this matrix are large (or, again, more formally, if the leading eigenvalue of the weight matrix is larger than 1.0), it can lead to a situation where the gradient signal is so large that it can cause learning to diverge. This is often referred to as exploding gradients.

These issues are the main motivation behind the LSTM model which introduces a new structure called a memory cell (see Figure 1 below). A memory cell is composed of four main elements: an input gate, a neuron with a self-recurrent connection (a connection to itself), a forget gate and an output gate. The self-recurrent connection has a weight of 1.0 and ensures that, barring any outside interference, the state of a memory cell can remain constant from one timestep to another. The gates serve to modulate the interactions between the memory cell itself and its environment. The input gate can allow incoming signal to alter the state of the memory cell or block it. On the other hand, the output gate can allow the state of the memory cell to have an effect on other neurons or prevent it. Finally, the forget gate can modulate the memory cell’s self-recurrent connection, allowing the cell to remember or forget its previous state, as needed.

Figure 1 : Illustration of an LSTM memory cell.

The equations below describe how a layer of memory cells is updated at every timestep . In these equations :

•  is the input to the memory cell layer at time 
• , , , , , , ,  and  are weight matrices
• , ,  and  are bias vectors

First, we compute the values for , the input gate, and  the candidate value for the states of the memory cells at time  :

Second, we compute the value for , the activation of the memory cells’ forget gates at time  :

Given the value of the input gate activation , the forget gate activation  and the candidate state value , we can compute  the memory cells’ new state at time  :

With the new state of the memory cells, we can compute the value of their output gates and, subsequently, their outputs :

Our model

The model we used in this tutorial is a variation of the standard LSTM model. In this variant, the activation of a cell’s output gate does not depend on the memory cell’s state . This allows us to perform part of the computation more efficiently (see the implementation note, below, for details). This means that, in the variant we have implemented, there is no matrix  and equation (5) is replaced by equation (7) :

Our model is composed of a single LSTM layer followed by an average pooling and a logistic regression layer as illustrated in Figure 2 below. Thus, from an input sequence , the memory cells in the LSTM layer will produce a representation sequence . This representation sequence is then averaged over all timesteps resulting in representation h. Finally, this representation is fed to a logistic regression layer whose target is the class label associated with the input sequence.

Figure 2 : Illustration of the model used in this tutorial. It is composed of a single LSTM layer followed by mean pooling over time and logistic regression.

Implementation note : In the code included this tutorial, the equations (1), (2), (3) and (7) are performed in parallel to make the computation more efficient. This is possible because none of these equations rely on a result produced by the other ones. It is achieved by concatenating the four matrices  into a single weight matrix  and performing the same concatenation on the weight matrices  to produce the matrix  and the bias vectors  to produce the vector . Then, the pre-nonlinearity activations can be computed with :

The result is then sliced to obtain the pre-nonlinearity activations for , , , and  and the non-linearities are then applied independently for each.

Code

The LSTM implementation can be found in the two following files :

• lstm.py : Main script. Defines and train the model.
• imdb.py : Secondary script. Handles the loading and preprocessing of the IMDB dataset.

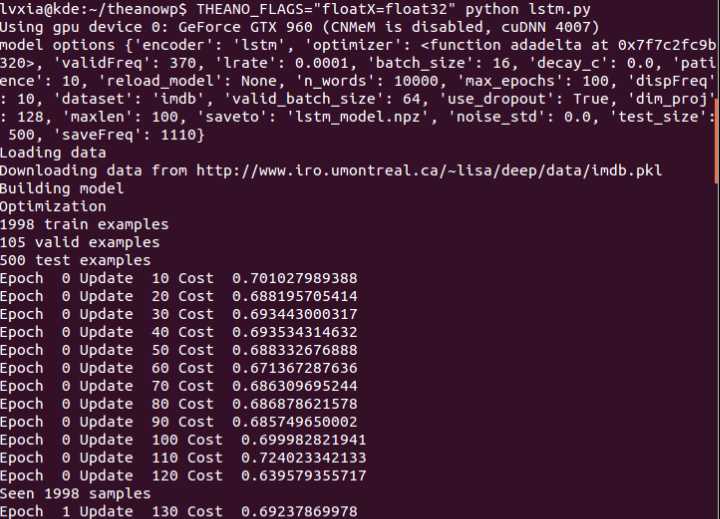
After downloading both scripts and putting both in the same folder, the user can run the code by calling:

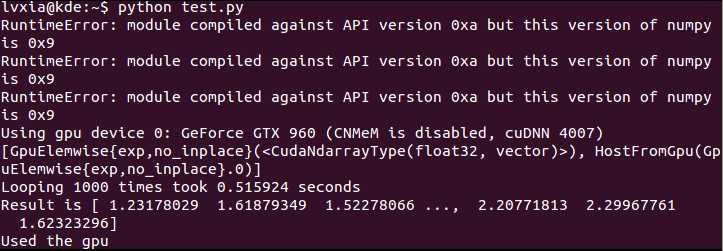
THEANO_FLAGS="floatX=float32" python lstm.py

The script will automatically download the data and decompress it.

Note : The provided code supports the Stochastic Gradient Descent (SGD), AdaDelta and RMSProp optimization methods. You are advised to use AdaDelta or RMSProp because SGD appears to performs poorly on this task with this particular model.

Papers

If you use this tutorial, please cite the following papers.

Introduction of the LSTM model:

• [pdf] Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.

Addition of the forget gate to the LSTM model:

• [pdf] Gers, F. A., Schmidhuber, J., & Cummins, F. (2000). Learning to forget: Continual prediction with LSTM. Neural computation, 12(10), 2451-2471.

More recent LSTM paper:

• [pdf] Graves, Alex. Supervised sequence labelling with recurrent neural networks. Vol. 385. Springer, 2012.

Papers related to Theano:

• [pdf] Bastien, Frédéric, Lamblin, Pascal, Pascanu, Razvan, Bergstra, James, Goodfellow, Ian, Bergeron, Arnaud, Bouchard, Nicolas, and Bengio, Yoshua. Theano: new features and speed improvements. NIPS Workshop on Deep Learning and Unsupervised Feature Learning, 2012.
• [pdf] Bergstra, James, Breuleux, Olivier, Bastien, Frédéric, Lamblin, Pascal, Pascanu, Razvan, Desjardins, Guillaume, Turian, Joseph, Warde-Farley, David, and Bengio, Yoshua. Theano: a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy), June 2010.

Thank you!

实验运行结果：

lstm.py

‘‘‘
Build a tweet sentiment analyzer
‘‘‘

from __future__ import print_function
import six.moves.cPickle as pickle

from collections import OrderedDict
import sys
import time

import numpy
import theano
from theano import config
import theano.tensor as tensor
from theano.sandbox.rng_mrg import MRG_RandomStreams as RandomStreams

import imdb

datasets = {‘imdb‘: (imdb.load_data, imdb.prepare_data)}

# Set the random number generators‘ seeds for consistency
SEED = 123
numpy.random.seed(SEED)

def numpy_floatX(data):
return numpy.asarray(data, dtype=config.floatX)

def get_minibatches_idx(n, minibatch_size, shuffle=False):
"""
Used to shuffle the dataset at each iteration.
"""

idx_list = numpy.arange(n, dtype="int32")

if shuffle:
numpy.random.shuffle(idx_list)

minibatches = []
minibatch_start = 0
for i in range(n // minibatch_size):
minibatches.append(idx_list[minibatch_start:
minibatch_start + minibatch_size])
minibatch_start += minibatch_size

if (minibatch_start != n):
# Make a minibatch out of what is left
minibatches.append(idx_list[minibatch_start:])

return zip(range(len(minibatches)), minibatches)

def get_dataset(name):
return datasets[name][0], datasets[name][1]

def zipp(params, tparams):
"""
When we reload the model. Needed for the GPU stuff.
"""
for kk, vv in params.items():
tparams[kk].set_value(vv)

def unzip(zipped):
"""
When we pickle the model. Needed for the GPU stuff.
"""
new_params = OrderedDict()
for kk, vv in zipped.items():
new_params[kk] = vv.get_value()
return new_params

def dropout_layer(state_before, use_noise, trng):
proj = tensor.switch(use_noise,
(state_before *
trng.binomial(state_before.shape,
p=0.5, n=1,
dtype=state_before.dtype)),
state_before * 0.5)
return proj

def _p(pp, name):
return ‘%s_%s‘ % (pp, name)

def init_params(options):
"""
Global (not LSTM) parameter. For the embeding and the classifier.
"""
params = OrderedDict()
# embedding
randn = numpy.random.rand(options[‘n_words‘],
options[‘dim_proj‘])
params[‘Wemb‘] = (0.01 * randn).astype(config.floatX)
params = get_layer(options[‘encoder‘])[0](options,
params,
prefix=options[‘encoder‘])
# classifier
params[‘U‘] = 0.01 * numpy.random.randn(options[‘dim_proj‘],
options[‘ydim‘]).astype(config.floatX)
params[‘b‘] = numpy.zeros((options[‘ydim‘],)).astype(config.floatX)

return params

def load_params(path, params):
pp = numpy.load(path)
for kk, vv in params.items():
if kk not in pp:
raise Warning(‘%s is not in the archive‘ % kk)
params[kk] = pp[kk]

return params

def init_tparams(params):
tparams = OrderedDict()
for kk, pp in params.items():
tparams[kk] = theano.shared(params[kk], name=kk)
return tparams

def get_layer(name):
fns = layers[name]
return fns

def ortho_weight(ndim):
W = numpy.random.randn(ndim, ndim)
u, s, v = numpy.linalg.svd(W)
return u.astype(config.floatX)

def param_init_lstm(options, params, prefix=‘lstm‘):
"""
Init the LSTM parameter:

:see: init_params
"""
W = numpy.concatenate([ortho_weight(options[‘dim_proj‘]),
ortho_weight(options[‘dim_proj‘]),
ortho_weight(options[‘dim_proj‘]),
ortho_weight(options[‘dim_proj‘])], axis=1)
params[_p(prefix, ‘W‘)] = W
U = numpy.concatenate([ortho_weight(options[‘dim_proj‘]),
ortho_weight(options[‘dim_proj‘]),
ortho_weight(options[‘dim_proj‘]),
ortho_weight(options[‘dim_proj‘])], axis=1)
params[_p(prefix, ‘U‘)] = U
b = numpy.zeros((4 * options[‘dim_proj‘],))
params[_p(prefix, ‘b‘)] = b.astype(config.floatX)

return params

def lstm_layer(tparams, state_below, options, prefix=‘lstm‘, mask=None):
nsteps = state_below.shape[0]
if state_below.ndim == 3:
n_samples = state_below.shape[1]
else:
n_samples = 1

assert mask is not None

def _slice(_x, n, dim):
if _x.ndim == 3:
return _x[:, :, n * dim:(n + 1) * dim]
return _x[:, n * dim:(n + 1) * dim]

def _step(m_, x_, h_, c_):
preact = tensor.dot(h_, tparams[_p(prefix, ‘U‘)])
preact += x_

i = tensor.nnet.sigmoid(_slice(preact, 0, options[‘dim_proj‘]))
f = tensor.nnet.sigmoid(_slice(preact, 1, options[‘dim_proj‘]))
o = tensor.nnet.sigmoid(_slice(preact, 2, options[‘dim_proj‘]))
c = tensor.tanh(_slice(preact, 3, options[‘dim_proj‘]))

c = f * c_ + i * c
c = m_[:, None] * c + (1. - m_)[:, None] * c_

h = o * tensor.tanh(c)
h = m_[:, None] * h + (1. - m_)[:, None] * h_

return h, c

state_below = (tensor.dot(state_below, tparams[_p(prefix, ‘W‘)]) +
tparams[_p(prefix, ‘b‘)])

dim_proj = options[‘dim_proj‘]
rval, updates = theano.scan(_step,
sequences=[mask, state_below],
outputs_info=[tensor.alloc(numpy_floatX(0.),
n_samples,
dim_proj),
tensor.alloc(numpy_floatX(0.),
n_samples,
dim_proj)],
name=_p(prefix, ‘_layers‘),
n_steps=nsteps)
return rval[0]

# ff: Feed Forward (normal neural net), only useful to put after lstm
# before the classifier.
layers = {‘lstm‘: (param_init_lstm, lstm_layer)}

def sgd(lr, tparams, grads, x, mask, y, cost):
""" Stochastic Gradient Descent

:note: A more complicated version of sgd then needed. This is
done like that for adadelta and rmsprop.

"""
# New set of shared variable that will contain the gradient
# for a mini-batch.
gshared = [theano.shared(p.get_value() * 0., name=‘%s_grad‘ % k)
for k, p in tparams.items()]
gsup = [(gs, g) for gs, g in zip(gshared, grads)]

# Function that computes gradients for a mini-batch, but do not
# updates the weights.
f_grad_shared = theano.function([x, mask, y], cost, updates=gsup,
name=‘sgd_f_grad_shared‘)

pup = [(p, p - lr * g) for p, g in zip(tparams.values(), gshared)]

# Function that updates the weights from the previously computed
# gradient.
f_update = theano.function([lr], [], updates=pup,
name=‘sgd_f_update‘)

return f_grad_shared, f_update

def adadelta(lr, tparams, grads, x, mask, y, cost):
"""
An adaptive learning rate optimizer

Parameters
----------
lr : Theano SharedVariable
Initial learning rate
tpramas: Theano SharedVariable
Model parameters
grads: Theano variable
Gradients of cost w.r.t to parameres
x: Theano variable
Model inputs
mask: Theano variable
Sequence mask
y: Theano variable
Targets
cost: Theano variable
Objective fucntion to minimize

Notes
-----
For more information, see [ADADELTA]_.

.. [ADADELTA] Matthew D. Zeiler, *ADADELTA: An Adaptive Learning
Rate Method*, arXiv:1212.5701.
"""

zipped_grads = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_grad‘ % k)
for k, p in tparams.items()]
running_up2 = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_rup2‘ % k)
for k, p in tparams.items()]
running_grads2 = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_rgrad2‘ % k)
for k, p in tparams.items()]

zgup = [(zg, g) for zg, g in zip(zipped_grads, grads)]
rg2up = [(rg2, 0.95 * rg2 + 0.05 * (g ** 2))
for rg2, g in zip(running_grads2, grads)]

f_grad_shared = theano.function([x, mask, y], cost, updates=zgup + rg2up,
name=‘adadelta_f_grad_shared‘)

updir = [-tensor.sqrt(ru2 + 1e-6) / tensor.sqrt(rg2 + 1e-6) * zg
for zg, ru2, rg2 in zip(zipped_grads,
running_up2,
running_grads2)]
ru2up = [(ru2, 0.95 * ru2 + 0.05 * (ud ** 2))
for ru2, ud in zip(running_up2, updir)]
param_up = [(p, p + ud) for p, ud in zip(tparams.values(), updir)]

f_update = theano.function([lr], [], updates=ru2up + param_up,
on_unused_input=‘ignore‘,
name=‘adadelta_f_update‘)

return f_grad_shared, f_update

def rmsprop(lr, tparams, grads, x, mask, y, cost):
"""
A variant of SGD that scales the step size by running average of the
recent step norms.

Parameters
----------
lr : Theano SharedVariable
Initial learning rate
tpramas: Theano SharedVariable
Model parameters
grads: Theano variable
Gradients of cost w.r.t to parameres
x: Theano variable
Model inputs
mask: Theano variable
Sequence mask
y: Theano variable
Targets
cost: Theano variable
Objective fucntion to minimize

Notes
-----
For more information, see [Hint2014]_.

.. [Hint2014] Geoff Hinton, *Neural Networks for Machine Learning*,
lecture 6a,
http://cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
"""

zipped_grads = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_grad‘ % k)
for k, p in tparams.items()]
running_grads = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_rgrad‘ % k)
for k, p in tparams.items()]
running_grads2 = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_rgrad2‘ % k)
for k, p in tparams.items()]

zgup = [(zg, g) for zg, g in zip(zipped_grads, grads)]
rgup = [(rg, 0.95 * rg + 0.05 * g) for rg, g in zip(running_grads, grads)]
rg2up = [(rg2, 0.95 * rg2 + 0.05 * (g ** 2))
for rg2, g in zip(running_grads2, grads)]

f_grad_shared = theano.function([x, mask, y], cost,
updates=zgup + rgup + rg2up,
name=‘rmsprop_f_grad_shared‘)

updir = [theano.shared(p.get_value() * numpy_floatX(0.),
name=‘%s_updir‘ % k)
for k, p in tparams.items()]
updir_new = [(ud, 0.9 * ud - 1e-4 * zg / tensor.sqrt(rg2 - rg ** 2 + 1e-4))
for ud, zg, rg, rg2 in zip(updir, zipped_grads, running_grads,
running_grads2)]
param_up = [(p, p + udn[1])
for p, udn in zip(tparams.values(), updir_new)]
f_update = theano.function([lr], [], updates=updir_new + param_up,
on_unused_input=‘ignore‘,
name=‘rmsprop_f_update‘)

return f_grad_shared, f_update

def build_model(tparams, options):
trng = RandomStreams(SEED)

# Used for dropout.
use_noise = theano.shared(numpy_floatX(0.))

x = tensor.matrix(‘x‘, dtype=‘int64‘)
mask = tensor.matrix(‘mask‘, dtype=config.floatX)
y = tensor.vector(‘y‘, dtype=‘int64‘)

n_timesteps = x.shape[0]
n_samples = x.shape[1]

emb = tparams[‘Wemb‘][x.flatten()].reshape([n_timesteps,
n_samples,
options[‘dim_proj‘]])
proj = get_layer(options[‘encoder‘])[1](tparams, emb, options,
prefix=options[‘encoder‘],
mask=mask)
if options[‘encoder‘] == ‘lstm‘:
proj = (proj * mask[:, :, None]).sum(axis=0)
proj = proj / mask.sum(axis=0)[:, None]
if options[‘use_dropout‘]:
proj = dropout_layer(proj, use_noise, trng)

pred = tensor.nnet.softmax(tensor.dot(proj, tparams[‘U‘]) + tparams[‘b‘])

f_pred_prob = theano.function([x, mask], pred, name=‘f_pred_prob‘)
f_pred = theano.function([x, mask], pred.argmax(axis=1), name=‘f_pred‘)

off = 1e-8
if pred.dtype == ‘float16‘:
off = 1e-6

cost = -tensor.log(pred[tensor.arange(n_samples), y] + off).mean()

return use_noise, x, mask, y, f_pred_prob, f_pred, cost

def pred_probs(f_pred_prob, prepare_data, data, iterator, verbose=False):
""" If you want to use a trained model, this is useful to compute
the probabilities of new examples.
"""
n_samples = len(data[0])
probs = numpy.zeros((n_samples, 2)).astype(config.floatX)

n_done = 0

for _, valid_index in iterator:
x, mask, y = prepare_data([data[0][t] for t in valid_index],
numpy.array(data[1])[valid_index],
maxlen=None)
pred_probs = f_pred_prob(x, mask)
probs[valid_index, :] = pred_probs

n_done += len(valid_index)
if verbose:
print(‘%d/%d samples classified‘ % (n_done, n_samples))

return probs

def pred_error(f_pred, prepare_data, data, iterator, verbose=False):
"""
Just compute the error
f_pred: Theano fct computing the prediction
prepare_data: usual prepare_data for that dataset.
"""
valid_err = 0
for _, valid_index in iterator:
x, mask, y = prepare_data([data[0][t] for t in valid_index],
numpy.array(data[1])[valid_index],
maxlen=None)
preds = f_pred(x, mask)
targets = numpy.array(data[1])[valid_index]
valid_err += (preds == targets).sum()
valid_err = 1. - numpy_floatX(valid_err) / len(data[0])

return valid_err

def train_lstm(
dim_proj=128, # word embeding dimension and LSTM number of hidden units.
patience=10, # Number of epoch to wait before early stop if no progress
max_epochs=5000, # The maximum number of epoch to run
dispFreq=10, # Display to stdout the training progress every N updates
decay_c=0., # Weight decay for the classifier applied to the U weights.
lrate=0.0001, # Learning rate for sgd (not used for adadelta and rmsprop)
n_words=10000, # Vocabulary size
optimizer=adadelta, # sgd, adadelta and rmsprop available, sgd very hard to use, not recommanded (probably need momentum and decaying learning rate).
encoder=‘lstm‘, # TODO: can be removed must be lstm.
saveto=‘lstm_model.npz‘, # The best model will be saved there
validFreq=370, # Compute the validation error after this number of update.
saveFreq=1110, # Save the parameters after every saveFreq updates
maxlen=100, # Sequence longer then this get ignored
batch_size=16, # The batch size during training.
valid_batch_size=64, # The batch size used for validation/test set.
dataset=‘imdb‘,

# Parameter for extra option
noise_std=0.,
use_dropout=True, # if False slightly faster, but worst test error
# This frequently need a bigger model.
reload_model=None, # Path to a saved model we want to start from.
test_size=-1, # If >0, we keep only this number of test example.
):

# Model options
model_options = locals().copy()
print("model options", model_options)

load_data, prepare_data = get_dataset(dataset)

print(‘Loading data‘)
train, valid, test = load_data(n_words=n_words, valid_portion=0.05,
maxlen=maxlen)
if test_size > 0:
# The test set is sorted by size, but we want to keep random
# size example. So we must select a random selection of the
# examples.
idx = numpy.arange(len(test[0]))
numpy.random.shuffle(idx)
idx = idx[:test_size]
test = ([test[0][n] for n in idx], [test[1][n] for n in idx])

ydim = numpy.max(train[1]) + 1

model_options[‘ydim‘] = ydim

print(‘Building model‘)
# This create the initial parameters as numpy ndarrays.
# Dict name (string) -> numpy ndarray
params = init_params(model_options)

if reload_model:
load_params(‘lstm_model.npz‘, params)

# This create Theano Shared Variable from the parameters.
# Dict name (string) -> Theano Tensor Shared Variable
# params and tparams have different copy of the weights.
tparams = init_tparams(params)

# use_noise is for dropout
(use_noise, x, mask,
y, f_pred_prob, f_pred, cost) = build_model(tparams, model_options)

if decay_c > 0.:
decay_c = theano.shared(numpy_floatX(decay_c), name=‘decay_c‘)
weight_decay = 0.
weight_decay += (tparams[‘U‘] ** 2).sum()
weight_decay *= decay_c
cost += weight_decay

f_cost = theano.function([x, mask, y], cost, name=‘f_cost‘)

grads = tensor.grad(cost, wrt=list(tparams.values()))
f_grad = theano.function([x, mask, y], grads, name=‘f_grad‘)

lr = tensor.scalar(name=‘lr‘)
f_grad_shared, f_update = optimizer(lr, tparams, grads,
x, mask, y, cost)

print(‘Optimization‘)

kf_valid = get_minibatches_idx(len(valid[0]), valid_batch_size)
kf_test = get_minibatches_idx(len(test[0]), valid_batch_size)

print("%d train examples" % len(train[0]))
print("%d valid examples" % len(valid[0]))
print("%d test examples" % len(test[0]))

history_errs = []
best_p = None
bad_count = 0

if validFreq == -1:
validFreq = len(train[0]) // batch_size
if saveFreq == -1:
saveFreq = len(train[0]) // batch_size

uidx = 0 # the number of update done
estop = False # early stop
start_time = time.time()
try:
for eidx in range(max_epochs):
n_samples = 0

# Get new shuffled index for the training set.
kf = get_minibatches_idx(len(train[0]), batch_size, shuffle=True)

for _, train_index in kf:
uidx += 1
use_noise.set_value(1.)

# Select the random examples for this minibatch
y = [train[1][t] for t in train_index]
x = [train[0][t]for t in train_index]

# Get the data in numpy.ndarray format
# This swap the axis!
# Return something of shape (minibatch maxlen, n samples)
x, mask, y = prepare_data(x, y)
n_samples += x.shape[1]

cost = f_grad_shared(x, mask, y)
f_update(lrate)

if numpy.isnan(cost) or numpy.isinf(cost):
print(‘bad cost detected: ‘, cost)
return 1., 1., 1.

if numpy.mod(uidx, dispFreq) == 0:
print(‘Epoch ‘, eidx, ‘Update ‘, uidx, ‘Cost ‘, cost)

if saveto and numpy.mod(uidx, saveFreq) == 0:
print(‘Saving...‘)

if best_p is not None:
params = best_p
else:
params = unzip(tparams)
numpy.savez(saveto, history_errs=history_errs, **params)
pickle.dump(model_options, open(‘%s.pkl‘ % saveto, ‘wb‘), -1)
print(‘Done‘)

if numpy.mod(uidx, validFreq) == 0:
use_noise.set_value(0.)
train_err = pred_error(f_pred, prepare_data, train, kf)
valid_err = pred_error(f_pred, prepare_data, valid,
kf_valid)
test_err = pred_error(f_pred, prepare_data, test, kf_test)

history_errs.append([valid_err, test_err])

if (best_p is None or
valid_err <= numpy.array(history_errs)[:,
0].min()):

best_p = unzip(tparams)
bad_counter = 0

print( (‘Train ‘, train_err, ‘Valid ‘, valid_err,
‘Test ‘, test_err) )

if (len(history_errs) > patience and
valid_err >= numpy.array(history_errs)[:-patience,
0].min()):
bad_counter += 1
if bad_counter > patience:
print(‘Early Stop!‘)
estop = True
break

print(‘Seen %d samples‘ % n_samples)

if estop:
break

except KeyboardInterrupt:
print("Training interupted")

end_time = time.time()
if best_p is not None:
zipp(best_p, tparams)
else:
best_p = unzip(tparams)

use_noise.set_value(0.)
kf_train_sorted = get_minibatches_idx(len(train[0]), batch_size)
train_err = pred_error(f_pred, prepare_data, train, kf_train_sorted)
valid_err = pred_error(f_pred, prepare_data, valid, kf_valid)
test_err = pred_error(f_pred, prepare_data, test, kf_test)

print( ‘Train ‘, train_err, ‘Valid ‘, valid_err, ‘Test ‘, test_err )
if saveto:
numpy.savez(saveto, train_err=train_err,
valid_err=valid_err, test_err=test_err,
history_errs=history_errs, **best_p)
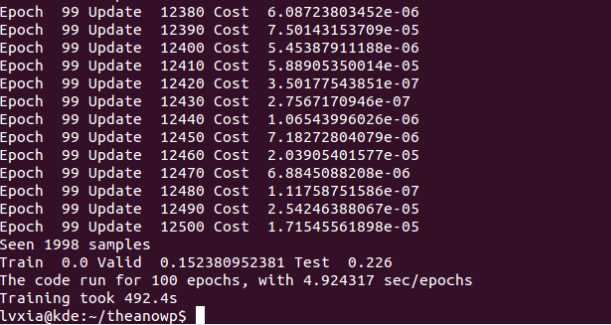
print(‘The code run for %d epochs, with %f sec/epochs‘ % (
(eidx + 1), (end_time - start_time) / (1. * (eidx + 1))))
print( (‘Training took %.1fs‘ %
(end_time - start_time)), file=sys.stderr)
return train_err, valid_err, test_err

if __name__ == ‘__main__‘:
# See function train for all possible parameter and there definition.
train_lstm(
max_epochs=100,
test_size=500,
)