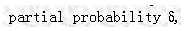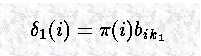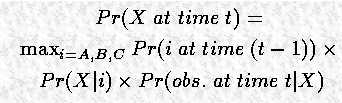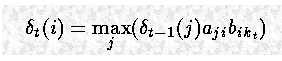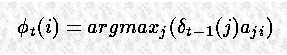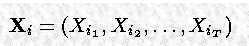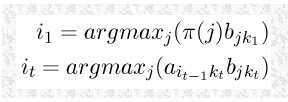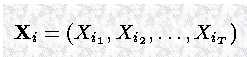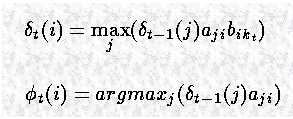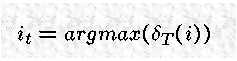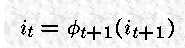标签:
Finding the most probable sequence of hidden states
给出一个HMM,以及某个观测序列,你可能想得到概率最大的那个隐式序列 sequence of hidden states.
1. Exhaustive search for a solution
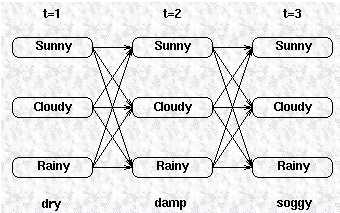
可以采用执行网格 Execution trellis 来对状态和 观测 observations 的关系可视化:
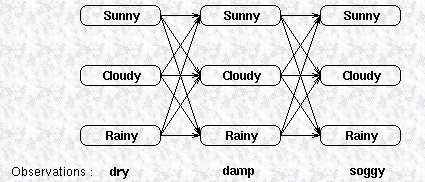
通过列出所有可能的隐式序列,并对每个序列计算以下概率,可以找到概率最大的隐式序列。

例如对于执行网格中的观测序列,可能的隐式序列概率:

这种方法很直观,可是计算量很大。与 forward algorithm 类似,我们也可以利用概率的时间不变性 time invariance of probabilities 来降低计算复杂度。
2. Reducint complexity using recursion
考虑通过递归的方法来找出最有可能的隐式序列。首先定义
(以下简称 Y),Y是到达某个中间状态的概率。
Partial probability Y 和在 forward algorithm中计算的不同,因为 Y 代表了在时间 t 到达某个状态的最有可能的路径的概率,而不是全部。
2a. Partial probabilities (Y) 和 Partial best paths
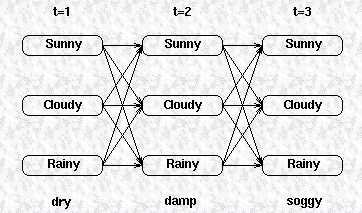
对于上述网格,每个 中间 和 终结 状态 (intermediate and terminating state),都有一个最有可能的路径到达该状态。例如:t=3 时,三个状态的最可能路径可能是这样的:
这些路径成为 partial best paths. 每个 Partial best paths 都有一个概率,称为 partial probability Y。
Y(i,t) 是所有在时间 t 到达状态 i 的所有序列中的最大概率,partial best path 是有最大概率的序列。
特别地,t = T 时,每个状态都有一个 partial probability 以及一个 partial best path。通过选择拥有最大的 partial probability 的路径,可以找出全局的最优路径 overall best path.
2b. Calculating Y‘s at time t=1
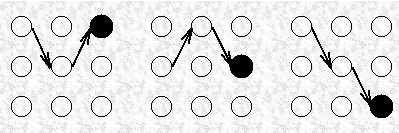
当 t = 1时,到达某状态的最可能路径是并不存在;不过可以使用 t=1时,系统在该状态,且观察状态在 k1的概率来计算:
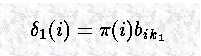
这和 forward algorithm 中的计算方法是一样的。
2c. Calculating Y‘s at time t > 1
计算时间 t 到达状态 X 的最可能路径,这个路径需要在时间 t-1 通过状态 A,B 或 C中的某一个。因此到达 X 的最可能路径是其中的一个:
我们希望找出以 AX, BX, CX 结尾的,拥有最大概率的序列。
Markov 假设当前状态的概率只依赖于前 n 个状态的,因此对于 first order markov assumption, X 在某序列发生的概率只依赖于前一个状态。因此以 AX 结尾的,最可能路径的概率是:
因此到 X 的最可能路径的概率是:
其中第一项是由 Y 在 t-1 时刻给出的,第二项是由 transition probabilities 给出的,第三项是由 observation probabilities 给出的。
将以上的公式一般化,可以得到在时间 t 到达状态 i 的 partial best path,且观测状态是 kt 的概率是:
2d. Back pointers, F‘s
在每个中间和终结状态 (intermediate and end state),我们都可以得到 partial probabilities, Y(i,t)。然而,我们的目标是在给定观测序列的情况下,找出最可能路径。因此我们需要某种记录下 partial best paths 的方式。
在计算 partial probability 的过程中,Y 在时间 t 的值,我们只需要知道 Y 在 t-1 时刻的值。在计算了这个 partial probability 的情况下,可以记录下是由哪一个状态产生的 Y(i,t) 的。这种记录方法通过为每个状态保持一个 back pointer F 来实现, F 指向上一个时刻产生当前 Y(i,t) 的那个状态。
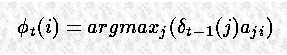
注意到这个表达式是从 Y 的上一个状态的值以及 transition probabilities 得到的,并不需要包含 observation probability (和计算 Y 是不一样的)。这是因为我们希望 F 可以解决 “通过那个路径最优可能到我所在的这个状态。”这个问题和 hidden states 有关,因由于观测产生的 confusing factors 可以忽略。
2e. Advantage of the approach
采用 Viterbi algorithm 对观测序列进行解码,有两个优势:
1. 计算复杂度降低了;
2. Viterbi algorithm 有很好的性质,可以在整个观测序列的基础上提供最好的解释。
另一种可以用来求得 执行序列的方法是:
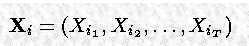
其中,
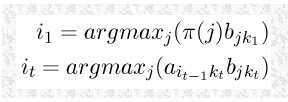
这种方法可能出现偏离正确答案的情况。
然而 Viterbi algorithm 会考虑整个观测序列,然后通过 F pointers (指针) 回溯 backtracking,找出最可能路径。
3. Section Summary
Viterbi algorithm 提供了一种计算方便的分析 HMM观测序列的方法,找出最可能序列。算法通过为每个节点计算 Partial Probability,同时使用一个 back-pointer F 指向如何到达该节点。 在完成计算后,就可以通过 后向指针 找到整个路径。
Definition
Viterbi algorithm definition
1. Formal definition of algorithm
对于 i = 1,。。。, n,
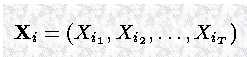
通过 初始隐式状态 (initial hidden state) 的概率以及观测概率 observation probabilities 可以计算 t=1 时的 partial probabilities.
对于 t=2,...,T,i=1,..., n,
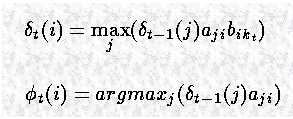
因此可以得到 到下一个状态的最可能路径,并记录下是如何到达该状态的。
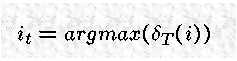
记录了在 t=T 时刻哪个状态是最可能的。
对于 t=T-1, ... , 1,
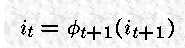
可以回溯得到整个最可能的路径。
2. Calculating individual Y‘s and F‘s
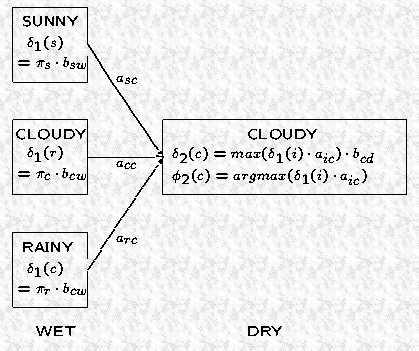
这里的计算方法和 forward algorithm 中的计算方法类似,不同之处在于 forward algorithm 中采用的是 summation 运算,而这里采用的是 max 运算。 在是因为 forward algorithm 是计算到达某个状态的总概率,而这里计算的是最大概率。
HMM系列之三:Viterbi Algorithm
标签:
原文地址:http://www.cnblogs.com/zhang123shuo/p/5674321.html