标签:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1000+10,INF=1000000;
int maze[MAXN][MAXN],d[MAXN][MAXN],sign[MAXN][MAXN]; //maze为保存input的数组,d为保存每个位置表面积的数组,sign为标记数组,判断是否进行dfs
int dx[4]={0,-1,0,1},dy[4]={1,0,-1,0}; //四方向遍历的数组
int squ=0,m,n; //使用全局变量是因为很多main函数中的变量在调用函数中也需要使用。
void dfs(int x,int y) //dfs函数作用是改变原来d数组中的表面积值。从而直接在main函数中累加出结果
{
sign[x][y]=0; //一开始将sign[x][y]归0,没有标记数组程序会停止工作。注: d数组减去表面积的值是依赖于周围
for(int i=0;i<4;i++) //的maze值,但是dfs在同一个位置只能执行一次。
{
int nx=x+dx[i],ny=y+dy[i];
if(nx>=0&&nx<m&&ny>=0&&ny<n) //判断是否越界。
{
if(maze[x][y]<=maze[nx][ny]) d[x][y]-=maze[x][y]; //如果比周围的要小,等于说那一个方向的面积全部被覆盖了。
else if(maze[x][y]>maze[nx][ny]) d[x][y]-=maze[nx][ny]; //如果比周围的要高,等于说那一个方向的面积需要去掉周围的高度值
if(sign[nx][ny]==INF) //只有未标记的maze需要dfs
dfs(nx,ny);
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&m,&n);
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
scanf("%d",&maze[i][j]);
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
d[i][j]=4*maze[i][j]+(maze[i][j]?1:0); //初始值为maze值乘侧面积也就是4,以及顶部的一块(分0和非0讨论)
sign[i][j]=INF; //标记初始全为INF
}
squ=0;
dfs(0,0);
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
squ+=d[i][j]; //计算剩下的表面积
printf("%d\n",squ);
}
return 0;
}
Description


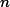


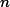

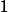

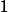



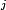

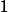



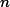

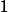








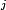


Input
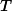
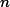


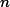




















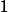

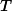



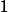

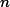










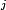




Output
Sample Input
2 3 3 1 0 0 3 1 2 1 1 0 3 3 1 0 1 0 0 0 1 0 1
Sample Output
30 20
本题目一开始没有头绪,整个的思路是比较乱的,样例我是数出结果的,甚至一开始还想过直接一整面一整面地求解,显然是不现实的。
然后想到了遍历,但具体几个方向遍历也有点问题,四个方向遍历肯定是需要的,但是否要向上遍历也是个问题。后来仔细想了一下,向上遍历无非就是再加4个侧面。
可能会觉得如果加上一块在上面,被挡住的侧面不就不同了么。实际上,四方向遍历改变的状态已经包括了挡住侧面的考虑。即为高度差。
一开始停止工作了,以为是数组越界了,实际上是没有加标记导致程序不停地执行bfs函数然后自然崩了,一开始我没加标记数组是因为我觉得加了标记数组后状态无法转移
到之前经过的状态会导致缺面积。实际上还是思路不清,每遍历到一个位置,改变的表面积是从初始值经过对周围砖块的高度判定来改变自身那一方向的面积的,也就是说周围的砖块仍然要对自身判断,而且没必要对同一方向的自己判断两次。所以,标记数组是必要的。
所以啊。做题之前一定要有整体的思路,再用代码实现。而且对不可能的方法要进行排除换别的方法。
别想着边想边敲了,我这个菜鸟。
标签:
原文地址:http://blog.csdn.net/huangjinlv/article/details/51919047