标签:style blog http color os io strong 数据
之前写线段树套splay数组版。。写了6.2k。。然后弃疗了。现在发现还是很水的。。嘎嘎。。
zju过不了,超时。
upd:才发现zju是多组数据。。TLE一版才发现。然后改了,MLE。。。手写内存池。。尼玛终于过了。。附zju2112代码于后。
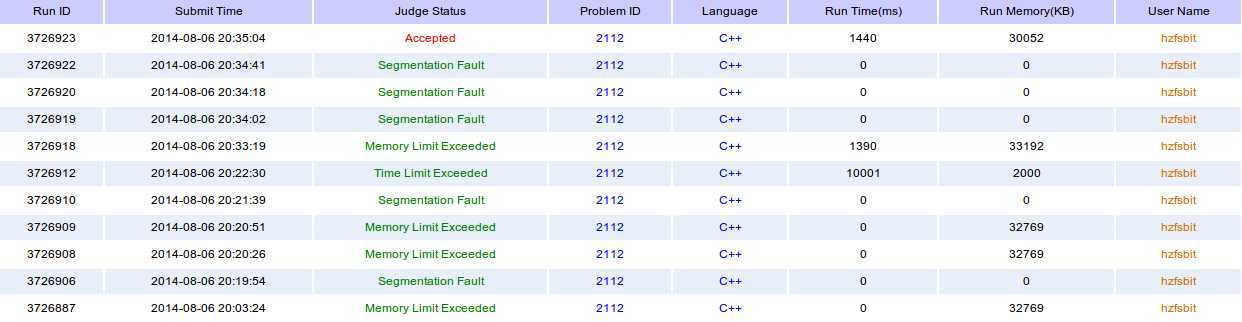
bzoj倒是过了,1A的感觉还是很爽的。。可是时间不好看。。这就是所谓\(O(nlog^3n)\)的复杂度的可怜之处么?
写挂的地方:
做法:线段树约束区间,平衡树支持修改和查询,没了。
修改:每次在包含点的线段树节点所包含的平衡树中删除要改的节点值,在插入新的值,\(O(log^2n)\)。
查询:由于无法直接查询,所以二分答案,求得答案在区间內的排名,等于各区间小于该值的节点数量,select直接搞,总共\(O(log^3n)\),具体可以先插入一个值节点,在求值节点的rank,最后删掉即可。
我是用线段树套treap。
然后树状数组套平衡树也可以过,常数小很多。。。
达成成就:AC树套树。

1 #include <cstdio> 2 #include <cstdlib> 3 #include <ctime> 4 #include <cstring> 5 typedef long long LL; 6 const int maxn = 10000 + 20; 7 int n, m, sum, a[maxn], INF = 0x3f3f3f3f; 8 struct treap_node { 9 treap_node *ch[2]; 10 int key, fix, cnt, size; 11 treap_node() { 12 ch[0] = ch[1] = NULL; 13 } 14 treap_node(int _key) { 15 ch[0] = ch[1] = NULL; 16 key = _key; 17 size = cnt = 1; 18 fix = rand(); 19 } 20 } *T[maxn << 2]; 21 inline void maintain(treap_node *t) { 22 t->size = t->cnt; 23 if(t->ch[0]) t->size += t->ch[0]->size; 24 if(t->ch[1]) t->size += t->ch[1]->size; 25 } 26 void rot(treap_node *&t, int d) { 27 treap_node *p = t->ch[d ^ 1]; 28 t->ch[d ^ 1] = p->ch[d], p->ch[d] = t; 29 maintain(t), maintain(p); 30 t = p; 31 } 32 void insert(treap_node *&t, int val) { 33 if(t == NULL) { 34 t = new treap_node(val); 35 } else { 36 if(val < t->key) { 37 insert(t->ch[0], val); 38 if(t->ch[0]->fix < t->fix) rot(t, 1); 39 } else if(t->key < val) { 40 insert(t->ch[1], val); 41 if(t->ch[1]->fix < t->fix) rot(t, 0); 42 } else 43 ++t->cnt; 44 } 45 maintain(t); 46 } 47 void del(treap_node *&t, int val) { 48 if(t->key == val) { 49 if(t->cnt == 1) { 50 if(!t->ch[0] || !t->ch[1]) { 51 treap_node *p = t; 52 if(!p->ch[0]) p = t->ch[1]; 53 else p = t->ch[0]; 54 delete t; 55 t = p; 56 } else { 57 int d = t->ch[0]->fix < t->ch[1]->fix; 58 rot(t, d); 59 del(t->ch[d], val); 60 } 61 } else --t->cnt; 62 } else del(t->ch[t->key < val], val); 63 if(t) maintain(t); 64 } 65 int select(treap_node *t, int val) { 66 if(t == NULL) return 0; 67 if(val < t->key) return select(t->ch[0], val); 68 int p = (t->ch[0]) ? t->ch[0]->size + t->cnt : t->cnt; 69 if(t->key < val) p += select(t->ch[1], val); 70 return p; 71 } 72 bool ok; 73 void query(int l, int r, int rt, int ql, int qr, int val) { 74 if(ql <= l && r <= qr) { 75 sum += select(T[rt], val); 76 return ; 77 } else { 78 int mid = (l + r) >> 1; 79 if(ql <= mid) query(l, mid, rt << 1, ql, qr, val); 80 if(mid < qr) query(mid + 1, r, rt << 1 | 1, ql, qr, val); 81 } 82 } 83 void seg_del(int l, int r, int rt, int pos, int val) { 84 del(T[rt], val); 85 if(l == r) return ; 86 int mid = (l + r) >> 1; 87 if(pos <= mid) seg_del(l, mid, rt << 1, pos, val); 88 else if(mid < pos) seg_del(mid + 1, r, rt << 1 | 1, pos, val); 89 } 90 void seg_insert(int l, int r, int rt, int pos, int val) { 91 insert(T[rt], val); 92 if(l == r) return ; 93 int mid = (l + r) >> 1; 94 if(pos <= mid) seg_insert(l, mid, rt << 1, pos, val); 95 else if(mid < pos) seg_insert(mid + 1, r, rt << 1 | 1, pos, val); 96 } 97 98 char gchar() { 99 char ret = getchar(); 100 for(; ret == ‘\n‘ || ret == ‘\r‘ || ret == ‘ ‘; ret = getchar()); 101 return ret; 102 } 103 int main() { 104 #ifndef ONLINE_JUDGE 105 freopen("data.in", "r", stdin), freopen("data.out", "w", stdout); 106 #endif 107 scanf("%d%d", &n, &m); 108 srand(n * m + 258); 109 for(int i = 1; i <= n; ++i) { 110 scanf("%d", &a[i]); 111 seg_insert(1, n, 1, i, a[i]); 112 } 113 ok = false; 114 for(int i = 1, p, b, c, d; i <= m; ++i) { 115 d = gchar(); 116 if(d == ‘C‘) { 117 scanf("%d%d", &p, &b); 118 seg_del(1, n, 1, p, a[p]); 119 a[p] = b; 120 seg_insert(1, n, 1, p, a[p]); 121 } else { 122 scanf("%d%d%d", &b, &c, &p); 123 LL l = 0, r = INF; 124 while(l < r) { 125 LL mid = (l + r) >> 1; 126 sum = 0; 127 query(1, n, 1, b, c, mid); 128 if(sum < p) { 129 l = mid + 1; 130 } else { 131 r = mid; 132 } 133 } 134 printf("%lld\n", l); 135 } 136 } 137 return 0; 138 }

1 #include <cstdio> 2 #include <cstdlib> 3 #include <ctime> 4 #include <cstring> 5 typedef long long LL; 6 const int maxn = 50000 + 1; 7 int n, m, sum, a[maxn], INF = 0x3f3f3f3f; 8 struct treap_node { 9 treap_node *ch[2]; 10 int key, fix, cnt, size; 11 treap_node() { 12 ch[0] = ch[1] = NULL; 13 } 14 treap_node(int _key) { 15 ch[0] = ch[1] = NULL; 16 key = _key; 17 size = cnt = 1; 18 fix = rand(); 19 } 20 } *T[maxn << 2]; 21 treap_node null_thing; 22 struct storage { 23 treap_node free_node[maxn * 18]; 24 int top, rec; 25 void init() { 26 rec = maxn * 18; 27 for(int i = 0; i < rec; ++i) free_node[top++] = i; 28 } 29 treap_node _new(int val) { 30 return free_node[--top] = treap_node(val); 31 } 32 void back_data() { 33 for(int i = top; i < rec; ++i) free_node[top++] = i; 34 } 35 }S; 36 37 inline void maintain(treap_node *t) { 38 t->size = t->cnt; 39 if(t->ch[0]) t->size += t->ch[0]->size; 40 if(t->ch[1]) t->size += t->ch[1]->size; 41 } 42 void rot(treap_node *&t, int d) { 43 treap_node *p = t->ch[d ^ 1]; 44 t->ch[d ^ 1] = p->ch[d], p->ch[d] = t; 45 maintain(t), maintain(p); 46 t = p; 47 } 48 void insert(treap_node *&t, int val) { 49 if(t == NULL) { 50 S._new(val); 51 t = &S.free_node[S.top]; 52 } else { 53 if(val < t->key) { 54 insert(t->ch[0], val); 55 if(t->ch[0]->fix < t->fix) rot(t, 1); 56 } else if(t->key < val) { 57 insert(t->ch[1], val); 58 if(t->ch[1]->fix < t->fix) rot(t, 0); 59 } else 60 ++t->cnt; 61 } 62 maintain(t); 63 } 64 void del(treap_node *&t, int val) { 65 if(t->key == val) { 66 if(t->cnt == 1) { 67 if(!t->ch[0] || !t->ch[1]) { 68 treap_node *p = t; 69 if(!p->ch[0]) p = t->ch[1]; 70 else p = t->ch[0]; 71 t = p; 72 } else { 73 int d = t->ch[0]->fix < t->ch[1]->fix; 74 rot(t, d); 75 del(t->ch[d], val); 76 } 77 } else --t->cnt; 78 } else del(t->ch[t->key < val], val); 79 if(t) maintain(t); 80 } 81 int select(treap_node *t, int val) { 82 if(t == NULL) return 0; 83 if(val < t->key) return select(t->ch[0], val); 84 int p = (t->ch[0]) ? t->ch[0]->size + t->cnt : t->cnt; 85 if(t->key < val) p += select(t->ch[1], val); 86 return p; 87 } 88 bool ok; 89 void query(int l, int r, int rt, int ql, int qr, int val) { 90 if(ql <= l && r <= qr) { 91 sum += select(T[rt], val); 92 return ; 93 } else { 94 int mid = (l + r) >> 1; 95 if(ql <= mid) query(l, mid, rt << 1, ql, qr, val); 96 if(mid < qr) query(mid + 1, r, rt << 1 | 1, ql, qr, val); 97 } 98 } 99 void seg_del(int l, int r, int rt, int pos, int val) { 100 del(T[rt], val); 101 if(l == r) return ; 102 int mid = (l + r) >> 1; 103 if(pos <= mid) seg_del(l, mid, rt << 1, pos, val); 104 else if(mid < pos) seg_del(mid + 1, r, rt << 1 | 1, pos, val); 105 } 106 void seg_insert(int l, int r, int rt, int pos, int val) { 107 insert(T[rt], val); 108 if(l == r) return ; 109 int mid = (l + r) >> 1; 110 if(pos <= mid) seg_insert(l, mid, rt << 1, pos, val); 111 else if(mid < pos) seg_insert(mid + 1, r, rt << 1 | 1, pos, val); 112 } 113 114 char gchar() { 115 char ret = getchar(); 116 for(; ret == ‘\n‘ || ret == ‘\r‘ || ret == ‘ ‘; ret = getchar()); 117 return ret; 118 } 119 void del_tree(int l, int r, int rt) { 120 T[rt] = NULL; 121 if(l == r) return ; 122 int mid = (l + r) >> 1; 123 del_tree(l, mid, rt << 1); 124 del_tree(mid + 1, r, rt << 1 | 1); 125 } 126 int main() { 127 128 int test_num; 129 scanf("%d", &test_num); 130 S.init(); 131 while(test_num--) { 132 S.back_data(); 133 scanf("%d%d", &n, &m); 134 del_tree(1, n, 1); 135 srand(n * m + 258); 136 for(int i = 1; i <= n; ++i) { 137 scanf("%d", &a[i]); 138 seg_insert(1, n, 1, i, a[i]); 139 } 140 ok = false; 141 for(int i = 1, p, b, c, d; i <= m; ++i) { 142 d = gchar(); 143 if(d == ‘C‘) { 144 scanf("%d%d", &p, &b); 145 seg_del(1, n, 1, p, a[p]); 146 a[p] = b; 147 seg_insert(1, n, 1, p, a[p]); 148 } else { 149 scanf("%d%d%d", &b, &c, &p); 150 LL l = 0, r = INF; 151 while(l < r) { 152 LL mid = (l + r) >> 1; 153 sum = 0; 154 query(1, n, 1, b, c, mid); 155 if(sum < p) { 156 l = mid + 1; 157 } else { 158 r = mid; 159 } 160 } 161 printf("%lld\n", l); 162 } 163 } 164 } 165 return 0; 166 }
BZOJ 1901: Zju2112 Dynamic Rankings 区间k大 带修改 在线 线段树套平衡树,布布扣,bubuko.com
BZOJ 1901: Zju2112 Dynamic Rankings 区间k大 带修改 在线 线段树套平衡树
标签:style blog http color os io strong 数据
原文地址:http://www.cnblogs.com/hzf-sbit/p/3895524.html