标签:style blog http color os io for art
LCS:给出两个序列S1和S2,求出的这两个序列的最大公共部分S3就是就是S1和S2的最长公共子序列了。公共部分
必须是以相同的顺序出现,但是不必要是连续的。
LCS具有最优子结构,且满足重叠子问题的性质。所以我们可以用动态规划来解决LCS问题。
由LCS问题的最优子结构可得出递归式:
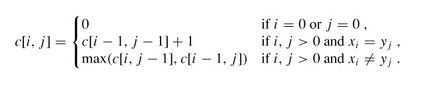
参考代码:

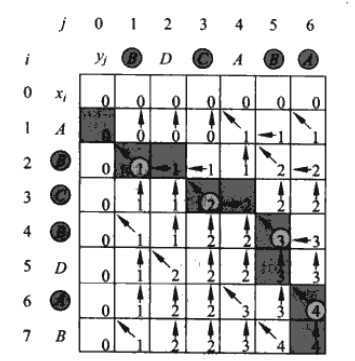
#include<iostream> using namespace std; #define M 7 #define N 6 int lcs(char *x,char *y,int c[M+1][N+1],int b[M+1][N+1]) { int m=M,n=N; for(int i=0;i<=m;i++) c[i][0]=0; for(int j=0;j<=n;j++) c[0][j]=0; for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { if(x[i]==y[j]) { c[i][j]=c[i-1][j-1]+1; b[i][j]=0; } else if(c[i-1][j]>=c[i][j-1]) { c[i][j]=c[i-1][j]; b[i][j]=1; } else { c[i][j]=c[i][j-1]; b[i][j]=-1; } } } return c[m][n]; } void printLcs(int b[][7],char *x,int i,int j) { if(i==0||j==0) { return; } if(b[i][j]==0) { printLcs(b,x,i-1,j-1); cout<<x[i]; } else if(b[i][j]==1) { printLcs(b,x,i-1,j); } else { printLcs(b,x,i,j-1); } } int main() { char x[M+1]={‘0‘,‘A‘,‘B‘,‘C‘,‘B‘,‘D‘,‘A‘,‘B‘}; char y[N+1]={‘0‘,‘B‘,‘D‘,‘C‘,‘A‘,‘B‘,‘A‘}; int c[M+1][N+1];//注意大小要为strlen+1;因为要存0 int b[M+1][N+1]; cout<<lcs(x,y,c,b)<<endl; cout<<"X:"<<x<<endl; cout<<"y:"<<y<<endl; for(int i=1;i<=7;i++) { for(int j=1;j<=6;j++) { cout<<b[i][j]<<ends; } cout<<endl; } cout<<"最长子序列为:"<<endl; printLcs(b,x,7,6); }
注意我们的b[0][i] b[i][0]没有存储任何东西。
输出:4
BCBA.
标签:style blog http color os io for art
原文地址:http://www.cnblogs.com/mmcmmc/p/3895565.html