标签:
学习汇编的过程中,一个很容易搞混的概念就是有符号数和无符号数的运算。
一个很自然的问题是,当对两个数做运算时(比如加法、减法),运算操作会因为两个符号有所不同吗?比如,我们都知道,在汇编里面,将两个数相加和相减,是这样的:
addl %eax, %edx
subl %eax, %edx
那么,这两个操作会因为有符号数、无符号数的差别而有不同吗?是不是有有符号的 addl 和无符号的 addl 呢?
在这里,只讨论 加、减、乘、除 四种操作,搞明白了这个,其他的就容易懂了。
对于上面问题的回答,答案是,对于加、减两种操作,处理器是不区分有符号数和无符号数的区别的,不管是有符号数还是无符号数,都是一样的操作。至于所操作的数是有符号还是无符号,那就看你如何看待这个数了。比如,对于一个四位的数: 1111 ,假如你把它看成有符号数,那么它就是 -1 ;假如你把它看成无符号数,那么它就是 15 。
在这种前提下,一个这样的指令: addl %eax, %edx ,其结果是固定的,并不会因为有符号数加法和无符号数加法而有不同的结果(处理器根本就不知道什么有符号和无符号数,你让它加,它就会按照我们所熟悉的加法操作那样一位一位地加,你让它减它就一位一位地减。只是,对于相加/相减的结果,会因为不同的解释(解释成有符号数还是无符号数)而有所不同。
比如,有两个三位数: 110 , 111 ,两者相加: addl %eax, %edx ,其结果是: 101 。假如看成无符号数,则是 5 ,假如看成有符号数,则是 -3 。
有一个很有意思的现象要提一提,那就是所谓的clock arithmetic:
对于这个三位数,最多只能表示八个数字:000, 001, 010, 011, 100, 101, 110, 111, 000, 010, ...
当达到111的时候,再往下加,又回到了000了。所以,可以把这八个数字串起来看做一个时钟:
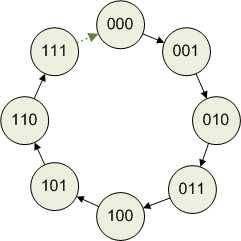
对于这个 101 三位数来说,将其看成无符号数,其值为5,将其看成有符号数其值为 -3;而clock arithmetic的意义就表现在,从000出发,往前(正方向)走5部和往后(负方向)走3部,其结果是一样的。
参考这里:http://igoro.com/archive/why-computers-represent-signed-integers-using-twos-complement/
接下来是乘法和除法。
对于乘法,其实处理器做的操作也是一样的。
容易引起混淆的是,在IA32中,有 MUL 和 IMUL 两个不同的乘法指令,前者用于无符号乘法,后者用于有符号乘法。
那么,为什么又说”处理器做的操作是一样的“呢?
这是因为,在乘法操作这一层上,处理器所做的操作确实是一样的。比如:
int a = -1; /*IA32中的二进制表示是 11111111 11111111 11111111 11111110 */ int b = -2; /* 11111111 11111111 11111111 11111101 */ int c = a * b /* 等于2, 二进制表示是 00000000 00000000 00000000 00000010 */ /* ----------------------- */ unsigned a = 429496729496; /* = 2^32 -2,和上面的表示一样: 11111111 11111111 11111111 11111110 */ unsigned b = 429496729495; /* 11111111 11111111 11111111 11111101 */ unsigned c = a * b; /* = 2 ,二进制表示和上面一样: 00000000 00000000 00000000 00000010 */
上面两个乘法操作,在汇编层面上的指令都很有可能会是这样子的(随便写的):
... movl $0xFFFFFFFE, %eax
movl $0xFFFFFFFD, %edx imul %eax, %edx ... ...
两者使用的都是相同的 IMUL 指令。实际上,两者产生的结果也是相同的。
那么,要 MUL 何用?为什么又要有两个不同的指令?答案是,对overflow flag有影响。在上面的有符号乘法中, -1 x -2 = 2这没错,也没有overflow;但是无符号乘法就有溢出了。对于这种情况,用 IMUL ,处理器就不会把这个看做是溢出,就不会在EFLAGS寄存器中设置overflow flag;但是如果用 MUL ,那么处理器就会看做是溢出,就会设置overflow flags。参考:http://igoro.com/archive/why-computers-represent-signed-integers-using-twos-complement/
对于除法,就真的是有区别了:http://www.tutorialspoint.com/assembly_programming/assembly_arithmetic_instructions.htm
对于overflow flag和carry flag,其实也差不多。容易引人困惑的是,有人说,overflow flag的设置发生于有符号数运算溢出时,carry flag的设置发生与无符号数运算的溢出时。为什么又牵扯到有符号和无符号?不是说加法和减法是不区分有符号和无符号的吗?
只需要记住这个就能明白:在一个算术运算中,overflow flag和carry flag可能会被同时设置。为什么呢?因为当把这个运算看成两个有符号数的运算时,就(有可能)会设置overflow flag;如果把这个运算看成是无符号数的运算时,就(有可能)会设置carry flag。换句话说,假如你在做有符号运算,看overflow flag就行,不用管carry flag;假如在做无符号运算,看carry flag就行,不用管overflow flag。可以参考这个很好的解释:http://teaching.idallen.com/dat2343/10f/notes/040_overflow.txt
这里摘录全文:
=====================================================
The CARRY flag and OVERFLOW flag in binary arithmetic
=====================================================
- Ian! D. Allen - idallen@idallen.ca - www.idallen.com
Do not confuse the "carry" flag with the "overflow" flag in integer
arithmetic. Each flag can occur on its own, or both together. The CPU‘s
ALU doesn‘t care or know whether you are doing signed or unsigned
mathematics; the ALU always sets both flags appropriately when doing any
integer math. The ALU doesn‘t know about signed/unsigned; the ALU just
does the binary math and sets the flags appropriately. It‘s up to you,
the programmer, to know which flag to check after the math is done.
If your program treats the bits in a word as unsigned numbers, you
must watch to see if your arithmetic sets the carry flag on, indicating
the result is wrong. You don‘t care about the overflow flag when doing
unsigned math. (The overflow flag is only relevant to signed numbers, not
unsigned.)
If your program treats the bits in a word as two‘s complement signed
values, you must watch to see if your arithmetic sets the overflow flag
on, indicating the result is wrong. You don‘t care about the carry
flag when doing signed, two‘s complement math. (The carry flag is only
relevant to unsigned numbers, not signed.)
In unsigned arithmetic, watch the carry flag to detect errors.
In unsigned arithmetic, the overflow flag tells you nothing interesting.
In signed arithmetic, watch the overflow flag to detect errors.
In signed arithmetic, the carry flag tells you nothing interesting.
English
-------
Do not confuse the English verb "to overflow" with the "overflow flag"
in the ALU. The verb "to overflow" is used casually to indicate that
some math result doesn‘t fit in the number of bits available; it could be
integer math, or floating-point math, or whatever. The "overflow flag"
is set specifically by the ALU as described below, and it isn‘t the same
as the casual English verb "to overflow".
In English, we may say "the binary/integer math overflowed the number
of bits available for the result, causing the carry flag to come on".
Note how this English usage of the verb "to overflow" is *not* the same as
saying "the overflow flag is on". A math result can overflow (the verb)
the number of bits available without turning on the ALU "overflow" flag.
Carry Flag
----------
The rules for turning on the carry flag in binary/integer math are two:
1. The carry flag is set if the addition of two numbers causes a carry
out of the most significant (leftmost) bits added.
1111 + 0001 = 0000 (carry flag is turned on)
2. The carry (borrow) flag is also set if the subtraction of two numbers
requires a borrow into the most significant (leftmost) bits subtracted.
0000 - 0001 = 1111 (carry flag is turned on)
Otherwise, the carry flag is turned off (zero).
* 0111 + 0001 = 1000 (carry flag is turned off [zero])
* 1000 - 0001 = 0111 (carry flag is turned off [zero])
In unsigned arithmetic, watch the carry flag to detect errors.
In signed arithmetic, the carry flag tells you nothing interesting.
Overflow Flag
-------------
The rules for turning on the overflow flag in binary/integer math are two:
1. If the sum of two numbers with the sign bits off yields a result number
with the sign bit on, the "overflow" flag is turned on.
0100 + 0100 = 1000 (overflow flag is turned on)
2. If the sum of two numbers with the sign bits on yields a result number
with the sign bit off, the "overflow" flag is turned on.
1000 + 1000 = 0000 (overflow flag is turned on)
Otherwise, the overflow flag is turned off.
* 0100 + 0001 = 0101 (overflow flag is turned off)
* 0110 + 1001 = 1111 (overflow flag is turned off)
* 1000 + 0001 = 1001 (overflow flag is turned off)
* 1100 + 1100 = 1000 (overflow flag is turned off)
Note that you only need to look at the sign bits (leftmost) of the three
numbers to decide if the overflow flag is turned on or off.
If you are doing two‘s complement (signed) arithmetic, overflow flag on
means the answer is wrong - you added two positive numbers and got a
negative, or you added two negative numbers and got a positive.
If you are doing unsigned arithmetic, the overflow flag means nothing
and should be ignored.
The rules for two‘s complement detect errors by examining the sign of
the result. A negative and positive added together cannot be wrong,
because the sum is between the addends. Since both of the addends fit
within the allowable range of numbers, and their sum is between them, it
must fit as well. Mixed-sign addition never turns on the overflow flag.
In signed arithmetic, watch the overflow flag to detect errors.
In unsigned arithmetic, the overflow flag tells you nothing interesting.
How the ALU calculates the Overflow Flag
----------------------------------------
This material is optional reading.
There are several automated ways of detecting overflow errors in two‘s
complement binary arithmetic (for those of you who don‘t like the manual
inspection method). Here are two:
Calculating Overflow Flag: Method 1
-----------------------------------
Overflow can only happen when adding two numbers of the same sign and
getting a different sign. So, to detect overflow we don‘t care about
any bits except the sign bits. Ignore the other bits.
With two operands and one result, we have three sign bits (each 1 or
0) to consider, so we have exactly 2**3=8 possible combinations of the
three bits. Only two of those 8 possible cases are considered overflow.
Below are just the sign bits of the two addition operands and result:
ADDITION SIGN BITS
num1sign num2sign sumsign
---------------------------
0 0 0
*OVER* 0 0 1 (adding two positives should be positive)
0 1 0
0 1 1
1 0 0
1 0 1
*OVER* 1 1 0 (adding two negatives should be negative)
1 1 1
We can repeat the same table for subtraction. Note that subtracting
a positive number is the same as adding a negative, so the conditions that
trigger the overflow flag are:
SUBTRACTION SIGN BITS
num1sign num2sign sumsign
---------------------------
0 0 0
0 0 1
0 1 0
*OVER* 0 1 1 (subtracting a negative is the same as adding a positive)
*OVER* 1 0 0 (subtracting a positive is the same as adding a negative)
1 0 1
1 1 0
1 1 1
A computer might contain a small logic gate array that sets the overflow
flag to "1" iff any one of the above four OV conditions is met.
A human need only remember that, when doing signed math, adding
two numbers of the same sign must produce a result of the same sign,
otherwise overflow happened.
Calculating Overflow Flag: Method 2
-----------------------------------
When adding two binary values, consider the binary carry coming into
the leftmost place (into the sign bit) and the binary carry going out
of that leftmost place. (Carry going out of the leftmost [sign] bit
becomes the CARRY flag in the ALU.)
Overflow in two‘s complement may occur, not when a bit is carried out
out of the left column, but when one is carried into it and no matching
carry out occurs. That is, overflow happens when there is a carry into
the sign bit but no carry out of the sign bit.
The OVERFLOW flag is the XOR of the carry coming into the sign bit (if
any) with the carry going out of the sign bit (if any). Overflow happens
if the carry in does not equal the carry out.
Examples (2-bit signed 2‘s complement binary numbers):
11
+01
===
00
- carry in is 1
- carry out is 1
- 1 XOR 1 = NO OVERFLOW
01
+01
===
10
- carry in is 1
- carry out is 0
- 1 XOR 0 = OVERFLOW!
11
+10
===
01
- carry in is 0
- carry out is 1
- 0 XOR 1 = OVERFLOW!
10
+01
===
11
- carry in is 0
- carry out is 0
- 0 XOR 0 = NO OVERFLOW
Note that this XOR method only works with the *binary* carry that goes
into the sign *bit*. If you are working with hexadecimal numbers, or
decimal numbers, or octal numbers, you also have carry; but, the carry
doesn‘t go into the sign *bit* and you can‘t XOR that non-binary carry
with the outgoing carry.
Hexadecimal addition example (showing that XOR doesn‘t work for hex carry):
8Ah
+8Ah
====
14h
The hexadecimal carry of 1 resulting from A+A does not affect the
sign bit. If you do the math in binary, you‘ll see that there is
*no* carry *into* the sign bit; but, there is carry out of the sign
bit. Therefore, the above example sets OVERFLOW on. (The example
adds two negative numbers and gets a positive number.)
--
| Ian! D. Allen - idallen@idallen.ca - Ottawa, Ontario, Canada
| Home Page: http://idallen.com/ Contact Improv: http://contactimprov.ca/
| College professor (Free/Libre GNU+Linux) at: http://teaching.idallen.com/
| Defend digital freedom: http://eff.org/ and have fun: http://fools.ca/
另外一个比较难缠的汇编问题: 那些在cmp后面来一个jg/jnle/jl/jnge的汇编到底在干什么?
在cmp后面来一个jmp就是conditional jump(同理,那些长得像cmovxxx的就是conditional move了),jump不jump是看cmp的结果是大于零还是等于零还是小于零。
这些jmp类型的指令都很self-explanatory:jg就是jump when greater,jl就是jump when less,jne就是jump when not equal......
cmp其实就等价于用一个数与另一个数做减法运算:
cmp dl, al 等价于:(注意这里采用的是AT&T的汇编格式)
al > dl
al - dl > dl -dl
al - dl > 0
很简单,就是做一个减法,看谁大,然后设置相应的flag (ZF,OF,SF,PF,CF)。也没有涉及到有符号和无符号。
但是有一个让人很头疼的地方就是,虽然cmp这个操作是和有符号/无符号无关的,依赖于cmp指令的众多的jmp中却有很多是和有符号/无符号有关的!
来看一个完整的列表:(摘自这里:http://unixwiz.net/techtips/x86-jumps.html)
| Instruction | Description | signed-ness | Flags | short jump opcodes | near jump opcodes |
|---|---|---|---|---|---|
| JO | Jump if overflow | OF = 1 | 70 | 0F 80 | |
| JNO | Jump if not overflow | OF = 0 | 71 | 0F 81 | |
| JS | Jump if sign | SF = 1 | 78 | 0F 88 | |
| JNS | Jump if not sign | SF = 0 | 79 | 0F 89 | |
| JE JZ |
Jump if equal Jump if zero |
ZF = 1 | 74 | 0F 84 | |
| JNE JNZ |
Jump if not equal Jump if not zero |
ZF = 0 | 75 | 0F 85 | |
| JB JNAE JC |
Jump if below Jump if not above or equal Jump if carry |
unsigned | CF = 1 | 72 | 0F 82 |
| JNB JAE JNC |
Jump if not below Jump if above or equal Jump if not carry |
unsigned | CF = 0 | 73 | 0F 83 |
| JBE JNA |
Jump if below or equal Jump if not above |
unsigned | CF = 1 or ZF = 1 | 76 | 0F 86 |
| JA JNBE |
Jump if above Jump if not below or equal |
unsigned | CF = 0 and ZF = 0 | 77 | 0F 87 |
| JL JNGE |
Jump if less Jump if not greater or equal |
signed | SF <> OF | 7C | 0F 8C |
| JGE JNL |
Jump if greater or equal Jump if not less |
signed | SF = OF | 7D | 0F 8D |
| JLE JNG |
Jump if less or equal Jump if not greater |
signed | ZF = 1 or SF <> OF | 7E | 0F 8E |
| JG JNLE |
Jump if greater Jump if not less or equal |
signed | ZF = 0 and SF = OF | 7F | 0F 8F |
| JP JPE |
Jump if parity Jump if parity even |
PF = 1 | 7A | 0F 8A | |
| JNP JPO |
Jump if not parity Jump if parity odd |
PF = 0 | 7B | 0F 8B | |
| JCXZ JECXZ |
Jump if %CX register is 0 Jump if %ECX register is 0 |
%CX = 0 %ECX = 0 |
E3 | |
Thanks.
:)
misc: 2's complement, signed / unsigned number,carry flags, and overflow flags
标签:
原文地址:http://www.cnblogs.com/walkerlala/p/5686014.html