标签:矩阵构造
题目链接: http://acm.nyist.net/JudgeOnline/problem.php?pid=298
题目大意:已知n个点(n<10000),现在对所有点进行以下操作:
平移一定距离(M),相对X轴上下翻转(X),相对Y轴左右翻转(Y),坐标缩小或放大一定的倍数(S),所有点对坐标原点逆时针旋转一定角度(R)。
操作的次数不超过1000000次,求最终所有点的坐标。
首先我们要知道矩阵乘法的概念。
在数学中,一个矩阵说穿了就是一个二维数组。一个n行m列的矩阵可以乘以一个m行p列的矩阵,得到的结果是一个n行p列的矩阵,其中的第i行第j列位置上的数等于前一个矩阵第i行上的m个数与后一个矩阵第j列上的m个数对应相乘后所有m个乘积的和。
比如,下面的算式表示一个2行2列的矩阵乘以2行3列的矩阵,其结果是一个2行3列的矩阵。其中,结果的那个4等于2*2+0*1:
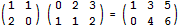
下面的算式则是一个1 x 3的矩阵乘以3 x 2的矩阵,得到一个1 x 2的矩阵:
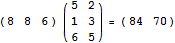
一个n行m列的矩阵可以乘以一个m行p列的矩阵,其时间的复杂性是O(m*p)。
矩阵乘法的两个重要性质:一,矩阵乘法不满足交换律;二,矩阵乘法满足结合律。为什么矩阵乘法不满足交换律呢?废话,交换过来后两个矩阵有可能根本不能相乘。为什么它又满足结合律呢?仔细想想你会发现这也是废话。假设你有三个矩阵A、B、C,那么(AB)C和A(BC)的结果的第i行第j列上的数都等于所有A(ik)*B(kl)*C(lj)的和(枚举所有的k和l)。
然后话题继续回到本题。
若是n个点,进行m次操作。要是直接模拟的话时间的复杂度是O(m*n)。
现在我们来进行矩阵的介绍:已知每个点的坐标是(x,y),构造一个矩阵3*1的矩阵来表示点。具体图如下:

我们能利用矩阵把m次操作(也就是不同的矩阵)在O(m)(准确来说是O(9*m))的操作里合并为一个矩阵,然后将这个矩阵与n个点组成的3*1的矩阵进行乘法运算,其复杂度为O(n)。于是我们就把复杂度从O(m*n)降到了O(m+n)。想想还是挺神的,原来没有想到过这样的用法。
下面是代码:
分别构造出类似于以上图片上面的代码,然后相乘,关键是!!尼玛矩阵要左乘呀,卡了两小时!!!!!!!!!!!!!!!
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<math.h>
#define PI acos(-1.0)
using namespace std;
struct Mat
{
double v[3][3];
};
Mat X,Y,M,S,R;
Mat operator * (Mat x,Mat y) //矩阵乘法
{
int i,j,k;
Mat tmp;
memset(tmp.v,0,sizeof(tmp.v));
for(i=0;i<3;i++)
for(j=0;j<3;j++)
for(k=0;k<3;k++)
tmp.v[i][j]+=x.v[i][k]*y.v[k][j];
return tmp;
}
void out(Mat A)
{
for(int i=0; i<3; i++)
{
for(int j=0; j<3; j++)
printf("%.0lf ",A.v[i][j]);
cout<<endl;
}
cout<<endl;
}
int main ()
{
int n,m;
scanf("%d%d",&n,&m);
double x[10005],y[10005];
char op;
Mat ans,org;
memset(org.v,0,sizeof(org.v));
for(int i=0; i<3; i++) org.v[i][i]=1;
ans=org;
Mat X,Y,M,S,R;
for(int i=0; i<n; i++)
scanf("%lf%lf",&x[i],&y[i]);
for(int j=0; j<m; j++)
{
getchar();
scanf("%c",&op);
if(op=='X')
{
X=org;
X.v[1][1]=-1;
ans=X*ans; //左乘!!!!!!!!!!!!!!!!!!!!!!
}
else if(op=='Y')
{
Y=org;
Y.v[0][0]=-1;
ans=Y*ans;
}
else if(op=='M')
{
M=org;
double vx,vy;
scanf("%lf%lf",&vx,&vy);
M.v[0][2]=vx;
M.v[1][2]=vy;
//out(M);
//out(ans);
ans=M*ans;
//ut(ans);
}
else if(op=='S')
{
S=org;
double k;
scanf("%lf",&k);
S.v[0][0]=k;
S.v[1][1]=k;
ans=S*ans;
}
else if(op=='R')
{
R=org;
double ar;
scanf("%lf",&ar);
R.v[0][0]= cos(ar/180.0*PI);
R.v[0][1]=-sin(ar/180.0*PI);
R.v[1][0]= sin(ar/180.0*PI);
R.v[1][1]= cos(ar/180.0*PI);
ans=R*ans;
}
}
for(int i=0; i<n; i++)
{
Mat tem;
//memset(tem.v,0,sizeof(tem.v));
tem.v[0][0]=x[i];
tem.v[1][0]=y[i];
tem.v[2][0]=1;
//out(tem);
tem=ans*tem; //左乘!!!!!!!!!!!!!!!!!!!!!
//out(tem);
printf("%.1lf %.1lf\n",tem.v[0][0],tem.v[1][0]);
}
}
标签:矩阵构造
原文地址:http://blog.csdn.net/u010468553/article/details/38405837