标签:
http://blog.csdn.net/libin56842/article/details/8530197
基础可以看上面这篇文章
风格:
maxn是题目给的最大区间,而节点数要开4倍,确切的说……
lson和rson辨别表示结点的左孩子和右孩子。
PushUp(int rt)是把当前结点的信息更新到父节点
PushDown(int rt)是把当前结点的信息更新给孩子结点。
rt表示当前子树的根(root),也就是当前所在的结点。
思想:
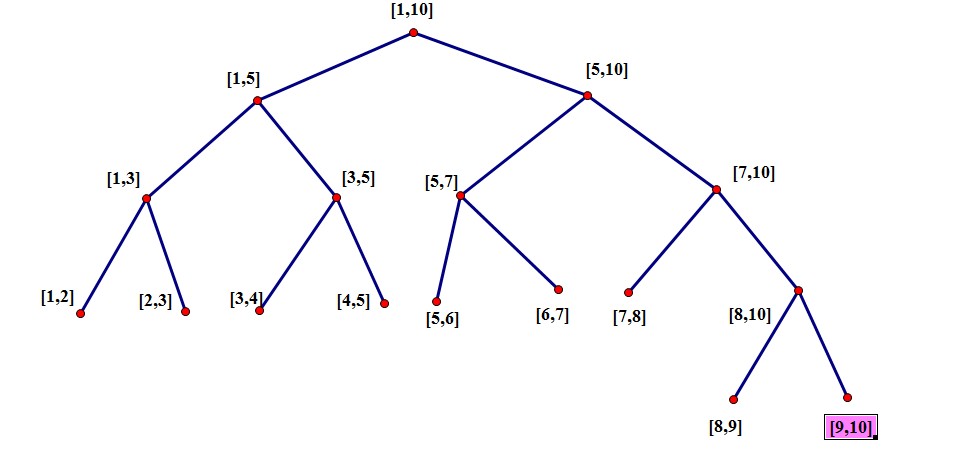
对于每个非叶节点所标示的结点 [a,b],其做孩子表示的区间是[a,(a+b)/2],其右孩子表示[(a+b)/2,b].
构造:
离散化和线段树:
题目:x轴上有若干个线段,求线段覆盖的总长度。
普通解法:设置坐标范围[min,max],初始化为0,然后每一段分别染色为1,最后统计1的个数,适用于线段数目少,区间范围小。
离散化的解法:离散化就是一一映射的关系,即将一个大坐标和小坐标进行一一映射,适用于线段数目少,区间范围大。
例如:[10000,22000],[30300,55000],[44000,60000],[55000,60000].
第一步:排序 10000 22000 30300 44000 55000 60000
第二部:编号 1 2 3 4 5 6
第三部:用编号来代替原数,即小数代大数 。
[10000,22000]~[1,2]
[30300,55000]~[3,5]
[44000,60000]~[4,6]
[55000,60000]~[5,6]
然后再用小数进行普通解法的步骤,最后代换回去。
线段树的解法:线段树通过建立线段,将原来染色O(n)的复杂度减小到 log(n),适用于线段数目多,区间范围小的情况。
离散化的线段树:适用于线段数目多,区间范围大的情况。
构造:
动态数据结构:
struct node{
node* left;
node* right;
……
}
静态全局数组模拟(完全二叉树):
struct node{
int left;
int right;
……
}Tree[MAXN]
http://www.xuebuyuan.com/1470670.html
线段树主要用四种用法
模板:
struct node { int l,r,c; }T[MAXN*4]; void PushUp(int rt) { T[rt].c = T[rt<<1].c + T[(rt<<1)+1].c; } void build(int l,int r,int x) { T[x].l = l; T[x].r = r; T[x].c = 0; if (l == r) return; int mid = (l+r)>>1; build(l,mid,x<<1); build(mid+1,r,(x<<1) + 1); } void update(int val,int l,int x) { if(T[x].l == T[x].r && T[x].l == l) { T[x].c += val; return; } int mid = (T[x].l + T[x].r)>>1; if (l > mid) { update(val,l,(x<<1) + 1); } else { update(val,l,x<<1); } PushUp(x); } int n,m,ans; void query(int l,int r,int x) { if(T[x].l == l && T[x].r == r) { ans += T[x].c; return; } int mid = (T[x].l + T[x].r)>>1; if (l > mid) { query(l,r,(x<<1)+1); } else if(r<=mid) { query(l,r,(x<<1)); } else { query(l,mid,(x<<1)); query(mid+1,r,(x<<1)+1); } }
HDU 1166
#include <iostream> #include <string> #include <cstring> #include <cstdlib> #include <cstdio> #include <cmath> #include <algorithm> #include <stack> #include <queue> #include <cctype> #include <vector> #include <iterator> #include <set> #include <map> #include <sstream> using namespace std; #define mem(a,b) memset(a,b,sizeof(a)) #define pf printf #define sf scanf #define spf sprintf #define pb push_back #define debug printf("!\n") #define MAXN 55555 #define MAX(a,b) a>b?a:b #define blank pf("\n") #define LL long long #define ALL(x) x.begin(),x.end() #define INS(x) inserter(x,x.begin()) #define pqueue priority_queue #define INF 0x3f3f3f3f struct node { int l,r,c; }T[MAXN*4]; void PushUp(int rt) { T[rt].c = T[rt<<1].c + T[(rt<<1)+1].c; } void build(int l,int r,int x) { T[x].l = l; T[x].r = r; T[x].c = 0; if (l == r) return; int mid = (l+r)>>1; build(l,mid,x<<1); build(mid+1,r,(x<<1) + 1); } void update(int val,int l,int x) { if(T[x].l == T[x].r && T[x].l == l) { T[x].c += val; return; } int mid = (T[x].l + T[x].r)>>1; if (l > mid) { update(val,l,(x<<1) + 1); } else { update(val,l,x<<1); } PushUp(x); } int n,m,ans; void query(int l,int r,int x) { if(T[x].l == l && T[x].r == r) { ans += T[x].c; return; } int mid = (T[x].l + T[x].r)>>1; if (l > mid) { query(l,r,(x<<1)+1); } else if(r<=mid) { query(l,r,(x<<1)); } else { query(l,mid,(x<<1)); query(mid+1,r,(x<<1)+1); } } int main() { int t,i,kase=1; char d[10]; sf("%d",&t); while(t--) { mem(T,0); pf("Case %d:\n",kase++); sf("%d",&n); build(1,n,1); for(i=1;i<=n;i++) { int tmp; sf("%d",&tmp); update(tmp,i,1); } while (sf("%s",d) != EOF) { if (d[0] == ‘E‘) break; int x, y; sf("%d%d", &x, &y); if (d[0] == ‘Q‘) { ans = 0; query(x,y,1); pf("%d\n",ans); } if (d[0] == ‘S‘) update(-y,x,1); if (d[0] == ‘A‘) update(y,x,1); } } return 0; }
标签:
原文地址:http://www.cnblogs.com/qlky/p/5690265.html