标签:
最近接触了不少机器学习的知识,我对人工智能领域相当感兴趣。人工神经网络是机器学习的一个重要领域;人工神经网络原理很简单,并没有什么深奥知识点和复杂的前导知识;于是自己动手实现一个简单的BP神经网络。
人工神经网络:神经网络就是一个有向图,这个有向图的顶点分三部分,一部分用于接收外界输入(输入层),一部分用于内部处理(隐含层),一部分用于输出结果(输出层);隐含层一般只有一层,因为随着隐含层的层数增加,神经网络的复杂性会成指数增加;一般现在应用神经网络的层数都不多,一般取一层就够了,现在最复杂的人工神经网络——谷歌大脑,它的隐层数目也只有5层;人工神经网络解决的是线性可分问题,凡是线性可分的解空间都可以用人工神经网络进行处理。
工作流程:假设输入层神经元个数为d,隐层神经元个数为q,输出层神经元个数为l;输入层到隐层的权值为vij(0<=i<d,0<=j<q)隐层到输出层的连接权为wjk(0<=j<q,0<=k<l);隐层的阈值为aj 输出层的阈值为bk;
输入层读入数据(xi),隐层把输入层的数据的加权值(xi*vij)累加,再减去阈值(aj)作为激发函数的输入值(Aj=f(∑(0=<i<d)Xi*vij-aj));输出层把隐层的数据加权(Aj*wjk)求和,输出层的值yk=f(∑(0<=j<q)Aj*wjk-bk)。
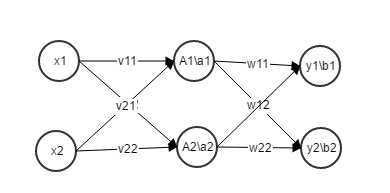
现在假设输入层的神经元个数为2,隐层神经元个数为2,输出层神经元个数为2(如下图)。
训练我们的神经网络:神经网络所学到的东西都包含在它的连接权与阈值中,训练一个神经网络也就是想办法调整它的各项连接权与阈值;调整阈值首先需要有一个目标,在这里我们的目标是使输出值尽可能的与样本标号(L)一致,我们采用均方误差Ek =1/2Σ(yj-Lj)2来衡量神经网络的分类效果。现在我们只需要使均方误差尽可能小就可以了,这样就把神经网络的参数调整转化为了最优化问题。最优化问题可以用梯度下降法进行求解。梯度下降法的推到过程在很多的机器学习书上都能找到,这里我就直接给出推导结果:
输出层梯度变化值: Δg[j] = y[j]*(1-y[j])*(L[k][j] - y[j]);
隐层梯度变化值: Δe[h] = A[h]*(1-A[h])*sum;
Δv[i][j] = u*e[j]*x[i];
Δa[i] = -u*e[i];
Δw[i][j] = u*g[j]*A[i];
Δb[i] = -u*g[i];
以下给出误差逆传播算法:
输入:训练集 D={(xk,yk)}mk=1
学习率 u
过程:在(0,1)范围内初始化网络中所有的连接权和阈值
repeat:
for all (Xk,yk) in D do
根据当前参数计算当前样本的输出yk;
计算输出层神经元梯度项gi;
计算隐层神经元梯度项ei;
更新连接权vij,aj,w,jk,bk;
end for
until 均方误差值达到要求精度或迭代次数超过允许计算的最大次数
算法实现代码:
public void train(int times,double er) { // TODO Auto-generated method stub int count=0; do{ count++; int k = -1; Er =0.0f; for(double[] x:D){ k++;//记录当前处理的数据的标号 E[k] = 0.0; for(int h=0;h<q;h++){ sum = 0.0f; for(int i=0;i<d;i++){//计算传入隐层每个节点的加权和 sum += v[i][h]*x[i]; } A[h] = (double) sigmoid.value(sum - a[h]);//计算隐层节点 } for(int h=0;h<l;h++){ sum =0.0f; for(int j =0;j<q;j++){//分别计算传到输出层的参数加权值 sum += w[j][h]*A[j];//sum += w[h][j]*A[h]; bug 1 } y[h] = (double) sigmoid.value(sum - b[h]);//计算输出值//计算均方误差 E[k] +=(L[k][h] - y[h])*(L[k][h] - y[h]); } E[k] *= (1.0)/2; //计算输出层神经元的梯度项 g for(int j =0;j< l;j++){ g[j] = y[j]*(1-y[j])*(L[k][j] - y[j]); } //计算隐层神经元的梯度项 e for(int h =0;h<q;h++){ sum = 0.0f; for(int j=0;j<l;j++){ sum += w[h][j]*g[j]; } e[h] = A[h]*(1-A[h])*sum; } //更新连接权 w,v 与阈值 a,b for(int i=0;i<q;i++){ a[i] += -u*e[i]; } for(int i=0;i<l;i++){ b[i] += -u*g[i]; } for(int i=0;i<d;i++){ for(int j =0;j<q;j++){ v[i][j] += u*e[j]*x[i]; } } for(int i=0;i<q;i++){ for(int j=0;j<l;j++){ w[i][j] += u*g[j]*A[i]; } } } Er = 0.0f; for(int i=0;i<E.length;i++){ Er += Math.abs(E[k]); } }while(Er >er&&count<times); }
现在用BP神经网络解决一个小小的线性分类问题:
double D[][] = {{0,0,},{0,1},{1,0},{1,1}};
double L[][] = {{1,0},{1,0},{1,0},{0,1}};
对平面上的四个点{0,0,},{0,1},{1,0},{1,1}进行分类,这里的输出标签为二元值:{1,0},{1,0},{1,0},{0,1}(y0 = 1表示标签为0 ,y1=1表示标签为1),输出层需要设计成两个神经元;如果输出标签是一元值{0,0,0,1},则输出层只需一个神经元。

import java.io.FileNotFoundException; import java.io.PrintWriter; import org.apache.commons.math3.analysis.function.Sigmoid; public class BP { //数据集:四个点; double D[][] = {{0,0,},{0,1},{1,0},{1,1}}; double L[][] = {{1,0},{1,0},{1,0},{0,1}}; double u = 0.1f;//学习率 Sigmoid sigmoid ; int d ;//输入层节点个数; int q ;//隐层节点个数; int l ;//输出层节点个数 //阈值 double[] a ; double[] b ; //连接权 double[][] v ;//输入到隐层 double[][] w ;//隐层到输出层 double sum = 0.0f; double[] A; double[] y; double[] e; double[] g; double[] E; double Er; double er; public double[][] getD(){ return D; } public double[][] getL(){ return L; } BP(int in ,int mid ,int out){ d = in;//输入层节点个数 q = mid;//隐层节点个数 l = out;//输出层节点个数 a = new double[q]; b = new double[l]; v = new double[d][q];//输入到隐层 w = new double[q][l];//隐层到输出层 sigmoid = new Sigmoid(); A = new double[q]; y = new double[l]; e = new double[q]; g = new double[l]; E = new double[D.length]; er = Er; iniRandom(); } public static void main(String[] args) { BP bp = new BP(2,4,2); bp.iniRandom(); bp.train(1000000,1.0E-1); bp.save("demo.txt"); } public void iniRandom(){ //在(0,1)范围内初始化网络中的所有阈值,连接权 for(int i=0;i<q;i++){ a[i] = (double) Math.random(); } for(int i=0;i<l;i++){ b[i] = (double) Math.random(); } for(int i=0;i<d;i++){ for(int j =0;j<q;j++){ v[i][j] = (double) Math.random(); } } for(int i=0;i<q;i++){ for(int j=0;j<l;j++){ w[i][j] = (double) Math.random(); } } } public void train(int times,double er) { // TODO Auto-generated method stub int count=0; do{ count++; int k = -1; Er =0.0f; for(double[] x:D){ k++;//记录当前处理的数据的标号 E[k] = 0.0; for(int h=0;h<q;h++){ sum = 0.0f; for(int i=0;i<d;i++){//计算传入隐层每个节点的加权和 sum += v[i][h]*x[i]; } A[h] = (double) sigmoid.value(sum - a[h]);//计算隐层节点 } for(int h=0;h<l;h++){ sum =0.0f; for(int j =0;j<q;j++){//分别计算传到输出层的参数加权值 sum += w[j][h]*A[j];//sum += w[h][j]*A[h]; bug 1 } y[h] = (double) sigmoid.value(sum - b[h]);//计算输出值 //计算均方误差 E[k] +=(L[k][h] - y[h])*(L[k][h] - y[h]); } E[k] *= (1.0)/2; //计算输出层神经元的梯度项 g for(int j =0;j< l;j++){ g[j] = y[j]*(1-y[j])*(L[k][j] - y[j]); } //计算隐层神经元的梯度项 e for(int h =0;h<q;h++){ sum = 0.0f; for(int j=0;j<l;j++){ sum += w[h][j]*g[j]; } e[h] = A[h]*(1-A[h])*sum; } //更新连接权 w,v 与阈值 a,b for(int i=0;i<q;i++){ a[i] += -u*e[i]; } for(int i=0;i<l;i++){ b[i] += -u*g[i]; } for(int i=0;i<d;i++){ for(int j =0;j<q;j++){ v[i][j] += u*e[j]*x[i]; } } for(int i=0;i<q;i++){ for(int j=0;j<l;j++){ w[i][j] += u*g[j]*A[i]; } } } Er = 0.0f; for(int i=0;i<E.length;i++){ Er += Math.abs(E[k]); } }while(Er >er&&count<times); System.out.println("y0\ty1"); for(int k =0;k<D.length;k++){ double[]x = D[k]; for(int h=0;h<q;h++){ sum = 0.0f; for(int i=0;i<d;i++){//计算传入隐层每个节点的加权和 sum += v[i][h]*x[i]; } A[h] = (double) sigmoid.value(sum - a[h]);//计算隐层节点 } for(int h=0;h<l;h++){ sum =0.0f; for(int j =0;j<q;j++){//分别计算传到输出层的参数加权值 sum += w[j][h]*A[j];//sum += w[h][j]*A[h]; bug 1 } y[h] = (double) sigmoid.value(sum - b[h]);//计算输出值 System.out.print(Math.round(y[h])+"\t"); } System.out.println(); } System.out.println(count+"-Er-"+Er); System.out.println(); } public void save(String filename){ PrintWriter out = null; try { out = new PrintWriter(filename); out.println(d+"\t"+q+"\t"+l); out.println("w[]:"); for(int i=0;i<w.length;i++){ for(int j=0;j<w[i].length;j++){ out.print(w[i][j]+"\t"); } out.println(); } out.println("a[]:"); for(int i=0;i<a.length;i++){ out.print(a[i]+"\t"); } out.println(); out.println("v[]:"); for(int i=0;i<v.length;i++){ for(int j =0;j<v[i].length;j++){ out.print(v[i][j]+"\t"); } out.println(); } out.println("b[]:"); for(int i=0;i<b.length;i++){ out.print(b[i]+"\t"); } } catch (FileNotFoundException e) { System.out.println("FileNotFound..."); }finally{ out.close(); } } }
运行结果:
y0 y1
1 0
1 0
1 0
0 1
1326-Er-0.09985477040289659
神经网络参数值:

2 4 2 w[]: 0.4734734334555844 0.4166439630989184 -0.16539393728354276 0.6905024328593287 -2.8796915544942725 2.43966901304918 -3.5478627812808825 3.948999341948662 a[]: 0.32063821958753613 0.6786843360467054 3.13511814629679 4.05368024148439 v[]: 0.8460297282417694 0.8832195045962835 2.18111507956042 2.759799840353552 -0.0373458145354313 0.933224930030448 2.152145920609395 2.7662226690924814 b[]: -3.296460577322894 4.123592764542515
设计BackPropagation类:上面的例程已经完全实现了BP神经网络,现在需要把它封装成一个类,以便于日后使用方便。
标签:
原文地址:http://www.cnblogs.com/yuanzhenliu/p/5644754.html