标签:
POJ2531 - Network Saboteur
POJ3009 - Curling 2.0
POJ3414 - Pots
题目大意:N个节点的完全图(2<=N<=20),以邻接矩阵C的形式给出节点两两之间连边的权值。现在需要将这些节点分为A、B两个子集,使得∑Cij (i∈A, j∈B)最大。
考虑到节点总数不超过20,所以直接枚举子集的复杂度O(2^N)是可以接受的,要更进一步节省时间的话,一来由于对称性可以把节点0固定在子集A内,二来在枚举子集A的时候一旦新加入一个元素就更新总和,不必到叶子节点再计算。

1 // Problem: poj2531 - Network Saboteur 2 // Category: Depth first search 3 // Author: Niwatori 4 // Date: 2016/07/19 5 6 #include <iostream> 7 using namespace std; 8 #define MAX(a,b) ((a)>(b)?(a):(b)) 9 10 int m[25][25], set1[25] = {0}, set2[25] = {0}; 11 int cnt1 = 0, cnt2 = 0, ans = 0; 12 13 void dfs(int lev, int n, int tot) 14 { 15 if (lev == n) 16 {ans = MAX(ans, tot); return;} 17 18 int tot1 = tot, tot2 = tot; 19 set1[cnt1++] = lev; 20 for (int i = 0; i < cnt2; ++i) 21 tot1 += m[lev][set2[i]]; 22 dfs(lev + 1, n, tot1); --cnt1; 23 24 set2[cnt2++] = lev; 25 for (int i = 0; i < cnt1; ++i) 26 tot2 += m[lev][set1[i]]; 27 dfs(lev + 1, n, tot2); --cnt2; 28 } 29 30 int main() 31 { 32 int n; cin >> n; 33 for (int i = 0; i < n; ++i) 34 for (int j = 0; j < n; ++j) 35 cin >> m[i][j]; 36 set1[cnt1++] = 0; // Fix node 0 37 dfs(1, n, 0); 38 cout << ans << endl; 39 return 0; 40 }
题目大意:在冰面上有一个小球,每次可以给小球指定一个运动方向,根据牛顿第一定律(雾)小球会一直沿着这个方向运动,直到碰到障碍物、终点或者出界,如果碰到障碍物那么障碍物会消失,如果出界则游戏失败。给定起点和终点,输出最少的运动次数(若超过10则输出-1),场地的长宽均不超过20。

图1:样例,S代表起点,G代表终点,阴影表示障碍物
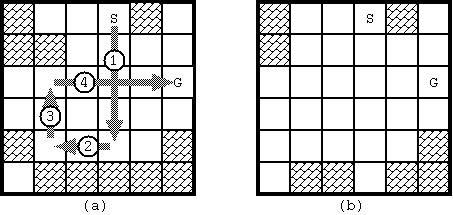
图2:样例的运动轨迹以及最终的场地状态
首先这道题要求的是最少次数,第一反应应当是bfs,但是考虑到每次运动之后,场地上的状态都会发生变化,记录场地状态所需要的空间开销过大,因而考虑dfs遍历所有可能的轨迹,选出其中最优的,且题目中「次数不超过10」是一个很明显的剪枝提示。估计一下总状态数最多为4^10大约10^7,搜索过程中及时剪掉那些不可行的运动方向可以大大缩小搜索状态空间,就一不小心AC了。

1 // Problem: poj3009 - Curling 2.0 2 // Category: Depth first search 3 // Author: Niwatori 4 // Date: 2016/07/19 5 6 #include <stdio.h> 7 #define MIN(a,b) ((a)<(b)?(a):(b)) 8 9 int nrow, ncol, ans, m[25][25]; 10 int dx[] = {1,0,-1,0}, dy[] = {0,1,0,-1}; 11 12 inline bool check(int x, int y) 13 { 14 if (x < 0 || x >= nrow || y < 0 || y >= ncol) return 0; 15 return m[x][y] != 1; 16 } 17 18 void dfs(int lev, int x, int y) 19 { 20 if (lev > 10) return; // Search terminated after 10 levels 21 for (int i = 0; i < 4; ++i) 22 { 23 int newx = x, newy = y, ok = 0; 24 while (check(newx + dx[i], newy + dy[i])) 25 { 26 newx += dx[i]; newy += dy[i]; 27 if (m[newx][newy] == 3) 28 {ans = MIN(lev, ans); ok = 1; break;} 29 } 30 31 // Circumstances of skipping direction i: 32 // 1. Reach the goal; 2. Unfeasible direction; 3. Out of range 33 int tmpx = newx + dx[i], tmpy = newy + dy[i]; 34 if (ok || (newx == x && newy == y)) continue; 35 if (tmpx < 0 || tmpx >= nrow || tmpy < 0 || tmpy >= ncol) continue; 36 37 m[tmpx][tmpy] = 0; // Blocks disappear 38 dfs(lev + 1, newx, newy); 39 m[tmpx][tmpy] = 1; // Backtrace 40 } 41 } 42 43 int main() 44 { 45 while (scanf("%d%d", &ncol, &nrow) == 2) 46 { 47 if (!nrow && !ncol) break; 48 int sr, sc; 49 for (int i = 0; i < nrow; ++i) 50 for (int j = 0; j < ncol; ++j) 51 { 52 scanf("%d", &m[i][j]); 53 if (m[i][j] == 2) {sr = i; sc = j;} 54 } 55 ans = 20; 56 dfs(1, sr, sc); 57 printf("%d\n", ans <= 10 ? ans : -1); 58 } 59 return 0; 60 }
题目大意:有两个容器,容积分别为A升和B升(1<=A, B<=100),允许以下三种操作:装满一个容器、倒空一个容器,将一个容器倒入另一个,求最少需要几步可以在一个容器中得到C升水,并输出任意一种可行的操作方案。
直接应用bfs即可,分别以两个容器中的水量作为访问数组的两个维度来判重。至于输出方案,由于笔者懒,所以就直接把操作步骤用字符串存起来放在队列里了,最后把它还原成输出的样式就可以啦。

1 // Problem: poj3414 - Pots 2 // Category: Breadth first search 3 // Author: Niwatori 4 // Date: 2016/07/19 5 6 #include <stdio.h> 7 #include <queue> 8 #include <string> 9 #define MIN(a,b) ((a)<(b)?(a):(b)) 10 #define MAX(a,b) ((a)>(b)?(a):(b)) 11 using std::string; 12 using std::queue; 13 14 struct node{ 15 int c1, c2; string steps; 16 node(int c1_, int c2_, string s_):c1(c1_),c2(c2_),steps(s_){} 17 }; 18 19 int main() 20 { 21 int A, B, C, vis[105][105] = {0}; 22 scanf("%d%d%d", &A, &B, &C); 23 24 queue<node> q; 25 q.push(node(0, 0, "")); 26 vis[0][0] = 1; 27 while (!q.empty()) 28 { 29 node now = q.front(); 30 if (now.c1 == C || now.c2 == C) break; q.pop(); 31 32 // Fill 33 if (!vis[A][now.c2]) 34 { 35 vis[A][now.c2] = 1; 36 q.push(node(A, now.c2, now.steps + "F1")); 37 } 38 if (!vis[now.c1][B]) 39 { 40 vis[now.c1][B] = 1; 41 q.push(node(now.c1, B, now.steps + "F2")); 42 } 43 44 // Drop 45 if (!vis[0][now.c2]) 46 { 47 vis[0][now.c2] = 1; 48 q.push(node(0, now.c2, now.steps + "D1")); 49 } 50 if (!vis[now.c1][0]) 51 { 52 vis[now.c1][0] = 1; 53 q.push(node(now.c1, 0, now.steps + "D2")); 54 } 55 56 // Pour 57 int newc1 = MAX(now.c1 - (B - now.c2), 0); 58 int newc2 = MIN(now.c1 + now.c2, B); 59 if (!vis[newc1][newc2]) 60 { 61 vis[newc1][newc2] = 1; 62 q.push(node(newc1, newc2, now.steps + "P1")); 63 } 64 newc1 = MIN(now.c1 + now.c2, A); 65 newc2 = MAX(now.c2 - (A - now.c1), 0); 66 if (!vis[newc1][newc2]) 67 { 68 vis[newc1][newc2] = 1; 69 q.push(node(newc1, newc2, now.steps + "P2")); 70 } 71 } 72 73 if (q.empty()) 74 printf("impossible"); 75 else 76 { 77 string s = q.front().steps; 78 printf("%d\n", s.length() / 2); 79 for (int i = 0; i < s.length(); i += 2) 80 switch (s[i]) 81 { 82 case ‘F‘: printf("FILL(%d)\n", s[i + 1] - ‘0‘); break; 83 case ‘D‘: printf("DROP(%d)\n", s[i + 1] - ‘0‘); break; 84 case ‘P‘: printf("POUR(%d,%d)\n", s[i + 1] - ‘0‘, 3 - (s[i + 1] - ‘0‘)); 85 } 86 } 87 return 0; 88 }
标签:
原文地址:http://www.cnblogs.com/niwatori1217/p/5692889.html