标签：
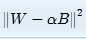给定w1-wn的值，α>=0，B可以等于1或者-1，求这个的最小值。定义运算：
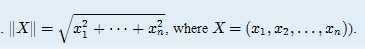。数学推论题，可以推出数学计算公式。
（w1-aB1）^2+（w2-aB2）^2+...（wn-aBn）^2
w1的取值范围是−10000≤wi≤10000，由于B1既可以取1也可以取-1，因此可以将所有的负数变为正数考虑。
因此：（|w1|-a）^2+（|w2|-a）^2+...（|wn|-a）^2（以后的w 全部为|w|，麻烦不想写）
又因为 要取最小值，显然 a=（w1+w2+...+wn）/n
展开式子 ： w1^2+a^2-2aw1
w2^2+a^2-2aw2
......
wn^2+a^2-2awn
得：（w1^2+w2^2+...+wn^2）+na^2-2a(w1+w2+...+wn)
将w1^2+w2^2+...+wn^2看作s1，w1+w2+...+wn看作s2，则：s1+na^2-2as2
且a=（w1+w2+...+wn）/n=s2/n
得 ： s1+n(s2/n)^2-2(s2/n)*s2=s1+s2^2/n-2(s2^2)/n=(ns1-s2^2)/n
附上代码：
#include <iostream> #include <cstdio> #include <cmath> #include <cstring> #define ll long long using namespace std; ll _gcd(ll x,ll y) { ll z; if(x<y) z=x,x=y,y=z; while(y) { z=x%y; x=y; y=z; } return x; } int xabs(int x) { return x>0?x:-x; } int main() { int T,i,j,n,m; scanf("%d",&T); while(T--) { scanf("%d",&n); ll aa,bb,t; ll s1=0,s2=0; for(i=0;i<n;i++) { scanf("%d",&m); m=xabs(m); s1+=m*m; s2+=m; } aa=n*s1-s2*s2; bb=n; t=_gcd(aa,bb); printf("%lld/%lld\n",aa/t,bb/t); } return 0; }
hdu 5734 Acperience（2016多校第二场）
标签：
原文地址：http://www.cnblogs.com/pshw/p/5694520.html
