标签:
题目大概说给一张无向点带有权无向图。定义连通图的权值为图中各点权的乘积,图的权值为其包含的各连通图的权和。设$z_i$为删除i点后图的权值,求$S = (\sum\limits_{i=1}^{n}i\cdot z_i) \text{ mod } (10^9 + 7)$。
官方题解这么说的:
显然, 只要删掉关键点才会使图不联通. 对于其他点, 权值很容易计算.
首先求出所有的点双联通分量, 对于每一个点双联通分量$S$, 新建一个节点$s$, 向$S$中每个节点$v$连边. 这样一来, 新增的点和原来图中的点会构成一个森林(据说这个有个名字, block forest data structure). 很容易观察到, 叶子节点肯定都是非关键点, 内部节点要么是关键点, 要么是新增的节点.
对于这个森林$F$, 删掉一个关键点或者一个叶子$i$之后, 会得到一个新森林$F_i$??, 这个$F_i$??对应的连通块集合和$G_i$对应的连通块集合其实是一样的(不考虑那些新增的点). 显然$G_i$的权值和$F_i$??的权值也是一样的, $F_i$的权值我们很容易通过树形dp算出来, 那么$G_i$的权值也随之而出.
可以在网上搜到关于用那个BF在线性时间计算所有关节点的影响的论文。。里面有这么一张图:
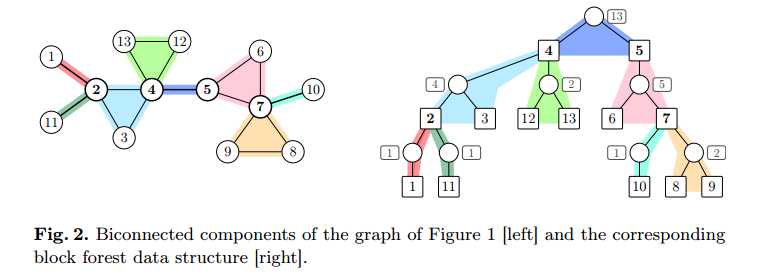
这样就好理解了。
设新加圆形结点的权为1,在那棵构造出来的树中用dp求出各个结点的两个信息:
最后通过枚举要删除的各个点,再加上乘法逆元搞搞,就能直接通过这两个信息很快地求出删除某结点后新的总权值。
另外。。有个地方空间开太小WA了好久。。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 #define MAXN 111111 6 #define MAXM 222222 7 8 struct Edge{ 9 int v,flag,next; 10 }edge[MAXM<<1]; 11 int NE,head[MAXN]; 12 void addEdge(int u,int v){ 13 edge[NE].v=v; edge[NE].flag=0; edge[NE].next=head[u]; 14 head[u]=NE++; 15 } 16 17 struct TEdge{ 18 int v,next; 19 }tEdge[MAXM<<4]; 20 int tNE,tHead[MAXN<<1]; 21 void addEdge(int u,int v,int nothing){ 22 tEdge[tNE].v=v; tEdge[tNE].next=tHead[u]; 23 tHead[u]=tNE++; 24 } 25 26 int dn,dfn[MAXN],low[MAXN]; 27 int stack[MAXM],top; 28 int root[MAXN],rn; 29 30 void tarjan(int u,int rt){ 31 dfn[u]=low[u]=++dn; 32 for(int i=head[u]; i!=-1; i=edge[i].next){ 33 if(edge[i].flag) continue; 34 edge[i].flag=edge[i^1].flag=1; 35 stack[++top]=i; 36 37 int v=edge[i].v; 38 39 if(dfn[v]){ 40 low[u]=min(low[u],dfn[v]); 41 continue; 42 } 43 44 tarjan(v,rt); 45 low[u]=min(low[u],low[v]); 46 47 if(low[v]>=dfn[u]){ 48 ++rn; 49 int k; 50 do{ 51 k=stack[top--]; 52 root[edge[k].v]=rt; 53 root[edge[k^1].v]=rt; 54 addEdge(rn,edge[k].v,0); 55 addEdge(edge[k].v,rn,0); 56 addEdge(rn,edge[k^1].v,0); 57 addEdge(edge[k^1].v,rn,0); 58 }while(edge[k^1].v!=u); 59 } 60 } 61 } 62 63 int n,weight[MAXN]; 64 65 bool vis[MAXN<<1]; 66 long long sum[MAXN<<1],pro[MAXN<<1]; 67 void dfs(int u){ 68 vis[u]=1; 69 sum[u]=0; pro[u]=(u<=n) ? weight[u] : 1; 70 for(int i=tHead[u]; i!=-1; i=tEdge[i].next){ 71 int v=tEdge[i].v; 72 if(vis[v]) continue; 73 dfs(v); 74 if(u<=n){ 75 sum[u]+=pro[v]; 76 sum[u]%=1000000007; 77 } 78 pro[u]*=pro[v]; 79 pro[u]%=1000000007; 80 } 81 } 82 83 long long ine(long long x){ 84 long long res=1; 85 int n=1000000007-2; 86 while(n){ 87 if(n&1){ 88 res*=x; res%=1000000007; 89 } 90 x*=x; x%=1000000007; 91 n>>=1; 92 } 93 return res; 94 } 95 96 int main(){ 97 int t,m; 98 scanf("%d",&t); 99 while(t--){ 100 scanf("%d%d",&n,&m); 101 for(int i=1; i<=n; ++i){ 102 scanf("%d",weight+i); 103 } 104 105 NE=0; 106 memset(head,-1,sizeof(head)); 107 int a,b; 108 while(m--){ 109 scanf("%d%d",&a,&b); 110 addEdge(a,b); 111 addEdge(b,a); 112 } 113 114 dn=0; memset(dfn,0,sizeof(dfn)); 115 rn=n; memset(root,0,sizeof(root)); 116 top=0; 117 tNE=0; memset(tHead,-1,sizeof(tHead)); 118 for(int i=1; i<=n; ++i){ 119 if(dfn[i]==0) tarjan(i,rn+1); 120 } 121 122 long long tot=0; 123 124 memset(vis,0,sizeof(vis)); 125 for(int i=1; i<=n; ++i){ 126 if(vis[i]) continue; 127 if(root[i]){ 128 dfs(root[i]); 129 tot+=pro[root[i]]; 130 tot%=1000000007; 131 }else{ 132 tot+=weight[i]; 133 tot%=1000000007; 134 } 135 } 136 137 long long ans=0; 138 139 for(int i=1; i<=n; ++i){ 140 if(root[i]){ 141 ans+=(tot-pro[root[i]]+pro[root[i]]*ine(pro[i])%1000000007+sum[i])%1000000007*i; 142 ans%=1000000007; 143 }else{ 144 ans+=(tot-weight[i])*i; 145 ans%=1000000007; 146 } 147 } 148 149 if(ans<0) ans+=1000000007; 150 printf("%lld\n",ans); 151 } 152 return 0; 153 }
HDU5739 Fantasia(点双连通分量 + Block Forest Data Structure)
标签:
原文地址:http://www.cnblogs.com/WABoss/p/5696926.html