标签:
二项分布:
基于最基础的一个离散型随机变量——伯努利随机变量X,我们进行n次重复的实验,其概率分布结果就是所谓的二项分布。
具体点来说,就是某个实验成功的概率是p,现在我们进行n此时杨,设随机变量X表示n次实验后成功的次数,那么有如下分布列成立。
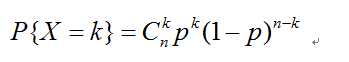
关于其期望,推导过程和几何分布、超几何分布中期望的推导是同质的,先退出X^k的表达式,然后根据二项式恒等关系,寻求自相似性建立递推关系,然后得到最终的期望值,由于之前已经给出了详细的推导过程,这里就不再赘述感兴趣的读者可以手动推导一下。
最后会得到这样一个式子:
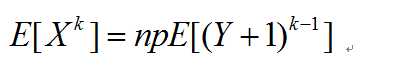
不难看出当k=1时,E[X]=np.
关于二项分布概率值的单调性这里有这样一个命题:对于满足参数为(n,p)的二项随机变量,k取得[0,n]时,P{X=k}先递增,后递减,当k = (n+1)p时取得最大值。
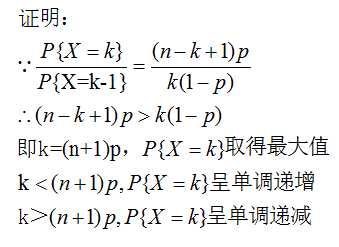
《A First Course in Probability》-chaper4-离散型随机变量-二项分布
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5697999.html