标签:
转自博客:http://blog.chinaunix.net/uid-24922718-id-4848418.html
尺取法就是两个指针表示区间[l,r]的开始与结束
然后根据题目来将端点移动,是一种十分有效的做法。适合连续区间的问题
poj3061
给定长度为n的数列整数a0,a1,a2,a3 ..... an-1以及整数S。求出综合不小于S的连续子序列的长度的最小值。如果解不存在,则输出0。
这里我们拿第一组测试数据举例子,即 n=10, S = 15, a = {5,1,3,5,10,7,4,9,2,8}
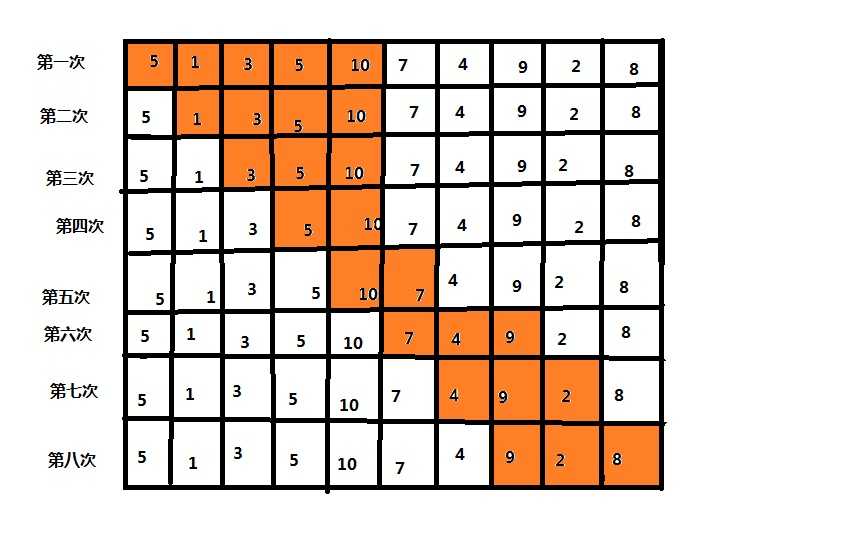
这幅图便是尺取法怎么“取”的过程了。
整个过程分为4布:
1.初始化左右端点
2.不断扩大右端点,直到满足条件
3.如果第二步中无法满足条件,则终止,否则更新结果
4.将左端点扩大1,然后回到第二步
用尺取法来优化,使复杂度降为了O(n)。
最后,再给一个尺取法的定义以便更好理解:返回的推进区间开头和结尾,求满足条件的最小区间的方法称为尺取法。
#include <stdio.h> int a[101000]; int main() { int n, n1, S, ans, z, y, i, t, s, sum; scanf("%d", &n); while(n--) { scanf("%d%d", &n1, &S); for(sum=0,i=1;i<=n1;i++) scanf("%d", &a[i]); ans = n1; sum=0; s = t = 1; while(1) { while(t<=n1&&sum<S) sum += a[t++]; if(s==1&&t>n1&&sum<S) { ans=0; break; } if(sum<S) break; if(ans>t-s) ans = t-s; sum -= a[s++]; } printf("%d\n", ans); } return 0; }
标签:
原文地址:http://www.cnblogs.com/Noevon/p/5698171.html