标签:
可以将这个图转换成森林来进行树形dp求解。看了这篇具体教学才会的:http://www.cnblogs.com/WABoss/p/5696926.html
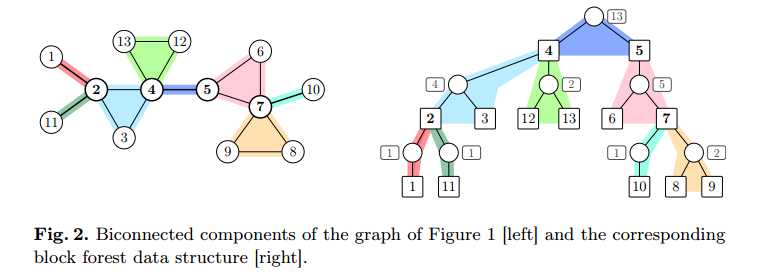
大致思路:求解一下点双连通分量(Tarjan),新构造一个节点连向这个分量中每一个节点。每个点双连通分量都这样构造好之后,原本连通的一张图就形成了一棵树,并且这个树中拿掉一个节点之后的连通性和原图相同!因此,可以在树上求解答案(树dp即可)。
注意:数据不一定保证原图是连通的,所以要特别注意原图中单个点的情况。
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<vector> #include<map> #include<set> #include<queue> #include<stack> #include<iostream> using namespace std; typedef long long LL; void File() { freopen("D:\\in.txt","r",stdin); freopen("D:\\out.txt","w",stdout); } inline int read() { char c = getchar(); while(!isdigit(c)) c = getchar(); int x = 0; while(isdigit(c)) { x = x * 10 + c - ‘0‘; c = getchar(); } return x; } const int maxn=200010; const LL mod=1e9+7; int h[maxn],tot; struct X { int u,v,nx; }e[2*maxn]; int pre[maxn],dfs_clock,low[maxn],bcc_cnt,bccno[maxn]; struct Edge { int u,v; Edge(int from,int to) { u=from; v=to; } }; stack<Edge> S; vector<int>bcc[maxn]; int T,n,m,be[2*maxn],block,sz,cnt[maxn]; bool f[maxn]; LL w[2*maxn],ans[maxn],val[maxn],SUM,pru[2*maxn]; int head[2*maxn]; struct Tree{ int u,v,nx; }tree[4*maxn]; int id; LL extend_gcd(LL a,LL b,LL &x,LL &y) { if(a==0&&b==0) return -1; if(b==0){x=1;y=0;return a;} LL d=extend_gcd(b,a%b,y,x); y-=a/b*x; return d; } LL mod_reverse(LL a) { LL x,y; LL d=extend_gcd(a,mod,x,y); if(d==1) return (x%mod+mod)%mod; else return -1; } void ADD(int a,int b) { tree[tot].u=a, tree[tot].v=b, tree[tot].nx=head[a], head[a]=tot++; } void AddEdge(int a,int b) { e[tot].u=a, e[tot].v=b, e[tot].nx=h[a], h[a]=tot++; } int Tarjan(int u,int fa) { int lowu=pre[u]=++dfs_clock; for(int i=h[u];i!=-1;i=e[i].nx) { int v=e[i].v; Edge e = Edge(u,v); if(!pre[v]) { S.push(e); int lowv=Tarjan(v,u); lowu=min(lowv,lowu); if(lowv>=pre[u]) { bcc_cnt++; id++; w[id]=1; for(;;) { Edge x = S.top();S.pop(); if(bccno[x.u]!=bcc_cnt) { ADD(x.u,id); ADD(id,x.u); be[id]=x.u; bccno[x.u]=bcc_cnt; } if(bccno[x.v]!=bcc_cnt) { ADD(x.v,id); ADD(id,x.v); be[id]=x.v; bccno[x.v]=bcc_cnt; } if(x.u==u&&x.v==v) break; } } } else if(pre[v]<pre[u]&&v!=fa) { S.push(e); lowu=min(lowu,pre[v]); } } return lowu; } void find_bcc() { memset(pre,0,sizeof(pre)); memset(bccno,0,sizeof(bccno)); dfs_clock=bcc_cnt=0; for(int i=1;i<=n;i++) if(!pre[i]) Tarjan(i,-1); } void dfs(int x) { sz++; f[x]=1; be[x]=block; for(int i=h[x];i!=-1;i=e[i].nx) if(!f[e[i].v]) dfs(e[i].v); } void dp(int x) { f[x]=1; pru[x]=w[x]; LL s=0; for(int i=head[x];i!=-1;i=tree[i].nx) { if(f[tree[i].v]) continue; dp(tree[i].v); pru[x]=(pru[x]*pru[tree[i].v])%mod; s=(s+pru[tree[i].v])%mod; } s=(s+val[be[x]]*mod_reverse(pru[x])%mod)%mod; ans[x]=((SUM-val[be[x]]+mod)%mod+s)%mod; } int main() { scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) w[i]=(LL)read(); memset(h,-1,sizeof h); tot=0; for(int i=1;i<=m;i++) { int u=read(),v=read(); AddEdge(u,v); AddEdge(v,u); } memset(f,block=sz=0,sizeof f); for(int i=1;i<=n;i++) { if(f[i]) continue; block++; sz=0; dfs(i); cnt[block]=sz; } SUM=0; for(int i=1;i<=block;i++) val[i]=1; for(int i=1;i<=n;i++) val[be[i]]=(val[be[i]]*w[i])%mod; for(int i=1;i<=block;i++) SUM=(SUM+val[i])%mod; memset(head,-1,sizeof head); tot=0; id=n; find_bcc(); memset(f,0,sizeof f); for(int i=1;i<=n;i++) if(cnt[be[i]]==1) ans[i]=(SUM-val[be[i]]+mod)%mod; for(int i=n+1;i<=id;i++) if(!f[i]) dp(i); LL S=0; for(int i=1;i<=n;i++) S=(S+((LL)i*ans[i])%mod)%mod; printf("%lld\n",S); } return 0; }
标签:
原文地址:http://www.cnblogs.com/zufezzt/p/5699182.html