快速幂取模的理解

标签：

快速幂的优越性（欢迎大家在此评论并提出您宝贵的建议）

                             常用公式：

                                         ( a + b  ) % c =  ( a % c + b% c ) % c
                                         ( a * b  ) % c  =  ( a % c * b% c ) % c

1：削减运算步骤，避免

如计算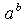，a=2,b=10;

     可以转换为   （a*a）的4次方   *   a的平方；

 具体转换步骤如右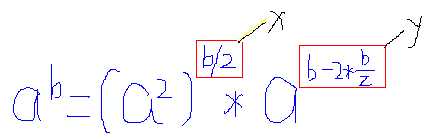：        由于b/2有小数丢失，故y存在（当b为偶数时，y=0）

                          具体代码如下(求n的m次方)(2的10次方)：      

                                                        __int64 fun(int n, int m)
                                                       {
                                                                __int64 ans=1, base=n;
                                                                while( m )
                                                               {
                                                                           if( m & 1 )/*为奇数时为真 */ ans = base * ans;
                                                                           base = base * base;
                                                                           m>>=1;//相当于 m=m/2
                                                                }
                                                                return ans;
                                                       }

                          过程如下：

2：快速幂求 n的m次方 的最右边一位，两位，三位等等是多少；

                 此处以求   a的b次方的最右边的三位数  为例，代码如下：

                                                     int fun(int a, int b)
                                                     {
                                                                int t, x;
                                                                x =a %1000;
                                                                t = 1;
                                                               while( b )
                                                               {
                                                                       if( b % 2 == 1 )
                                                                      {
                                                                              t *= x;
                                                                              t %= 1000;
                                                                       }
                                                                       x *= x;
                                                                       x %= 1000;
                                                                       b /= 2;
                                                               }
                                                      return t;
                                                      }

3：快速幂求模可避免数据超出范围；     

                          代码如下：

                                               int quickpow(int n,int m,int mod)
                                               {
                                                           int ans=1, base=n;
                                                           while( m )
                                                           {
                                                                      if( m & 1 )//m为奇数时为真 等于  m%2
                                                                      {
                                                                                ans = ( base * ans ) % mod;
                                                                      }
                                                                      base = ( base * base) % mod;
                                                                      m >>= 1;//等于m = m / 2
                                                           }
                                                           return ans;
                                               }

快速幂取模的理解

标签：

原文地址：http://www.cnblogs.com/123tang/p/5699447.html