标签:二叉搜索树
二叉搜索树
二叉搜索树又被称为二叉查找树、二叉排序树。其具备以下性质:
1> 每一个节点都有一个作为搜索依据的关键码(key),并且互不相同
2>左节点的关键码都小于根结点的关键码
3>右节点的关键码都大于根结点的关键码
4>每个子树都满足二叉搜索树
具备以上性质,所以二叉搜索树的中序遍历是有序的。
2.二叉搜索树的构造
每个节点有一个key值和value值,key值是用来区分节点的,每个节点的key值都不相同。每个节点都
有指向左和右的指针。
template<class K, class V>
struct BSTreeNode
{
BSTreeNode(const K&key, const V&value)
:_left(NULL)
, _right(NULL)
, _key(key)
, _value(value)
{}
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(NULL)
{}
~BSTree()
{
if (_root)
{
clear();
}
}
protected:
Node* _root;
};3.二叉搜索树的插入
如果插入的时候是一颗空树,则new一个根结点出来,之后插入的时候根据key值来进行判断插入的位
置,每插入一个值都要从根节点开始判断,要插入的key值比根结点的key值小,则走左树,比根节点的
key值大,则走右树。直到找到正确的位置进行插入,返回true。当然与根节点的值相等的话返回false。
1>非递归的插入
bool insert(const K& key, const V&value)
{//遵循左小于根右大于根,每个子树都满足
if (_root == NULL)
{
_root = new Node(key, value);
return true;
}
Node*parent = NULL;
Node*cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
if (parent->_key > key)
{
parent->_left = new Node(key, value);
}
else
parent->_right = new Node(key, value);
return true;
}
2>递归插入
//进行递归插入,注意_insertR接收的root参数是引用类型的,
bool insertR(const K&key, const V&value)
{
return _insertR(_root, key, value);
}
protected:
bool _insertR(Node* &root, const K&key, const V&value)
{
if (root == NULL)//此时的root肯定是要插入的key值正确的位置,因为root是引用的
{
root = new Node(key, value);
return true;
}
if (root->_key > key)
{
_insertR(root->_left, key, value);
}
else if (root->_key < key)
{
_insertR(root->_right, key, value);
}
else
{
return false;
}
}
4.二叉搜索树的查找
二叉树最坏的查找情况时间复杂度为O(n);平均时间复杂度为O(log2(n))。
Node* find(const K&key)//找到的话返回该节点
{
assert(_root);
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return NULL;
}
5.二叉搜索树的删除
二叉搜索树的删除可分为三种情况:
1>要删除的节点的左树为空,右树可为空可不为空,这个节点可能为根节点,也可能为其他节点。
删一个普通的左树为空的节点。让该节点的父亲节点指向该节点的右节点,删除该节点。
删除这个树的8这个节点
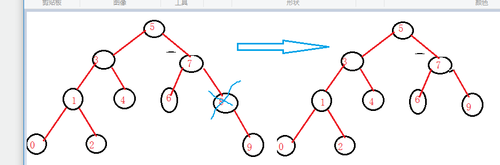
2>要删除的节点的右树为空,左树可为空可不为空,这个节点可能为根节点,也可能为其他节点。
删除的方法与右节点同理。这里不举例子了。
3>要删除的节点左右都不为空。
首先找到该节点右树的最左节点,然后与其交换,再删除最左节点。因为该节点右树的最左节点比
该节点左树的节点都大,比该节点右树的节点都小,满足二叉搜索树,所以用其与删除的节点交换。
1>非递归的删除
bool remove(const K&key)
{
if (_root == NULL)
return false;
Node* cur = _root;
Node* parent = NULL;
//找到要删除的节点
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
break;
}
}
if (cur == NULL)
{
return false;
}
Node* del;
//1.cur->left==NULL
if (cur->_left == NULL)
{
del = cur;
//删除的是根节点
if (parent == NULL)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
//2.cur->right=NULL
else if (cur->_right == NULL)
{
del = cur;
if (parent == NULL)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
else //左右不为空
{
parent = cur;
//找到右树的最左节点进行替换,这样的话还是满足二叉搜索树
Node* firstLeftN = cur->_right;
while (firstLeftN->_left)
{
parent= firstLeftN;
firstLeftN = firstLeftN->_left;
}
del = firstLeftN;
cur->_key = firstLeftN->_key;
cur->_value = firstLeftN->_value;
if (parent->_left == firstLeftN)
{
parent->_left = firstLeftN->_right;
}
else
{
parent->_right = firstLeftN->_right;
}
}
delete del;
return true;
}
2>递归的删除
bool removeR(const K&key)
{
return _removeR(_root, key);
}
bool _removeR(Node*& root, const K&key)
{
if (root == NULL)
{
return false;
}
if (root->_key < key)
{
_removeR(root->_right, key);
}
else if (root->_key>key)
{
_removeR(root->_left, key);
}
else
{
Node *del = root;
//1.要删的节点左为空
if (root->_left == NULL)
{
root = root->_right;
}
//右为空
else if (root->_right == NULL)
{
root = root->_left;
}
//左右不为空
else
{
Node*firstLeftN = root->_right;
while (firstLeftN->_left)
{
firstLeftN = firstLeftN->_left;
}
swap(root->_key, firstLeftN->_key);
swap(root->_value, firstLeftN->_value);
return _removeR(root->_right,key);
}
delete del;
return true;
}
}
本文出自 “学习历程” 博客,请务必保留此出处http://10541571.blog.51cto.com/10531571/1829668
标签:二叉搜索树
原文地址:http://10541571.blog.51cto.com/10531571/1829668