标签:
【题目大意】
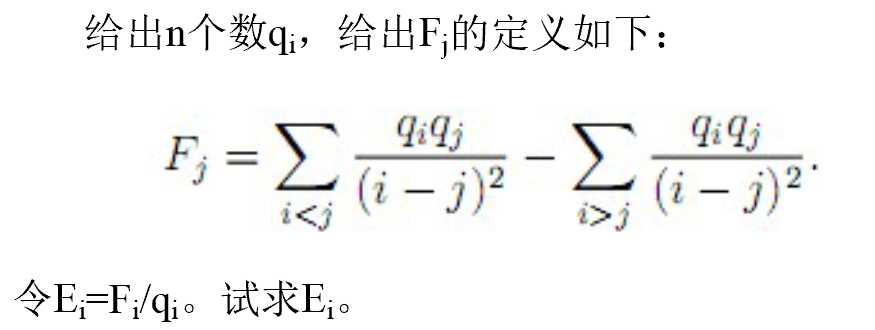
【思路】
很好这很FFT……
想了半天也没明白到底什么是卷积∑的上下界,我当初学的时候没说一定要从0开始啊quq
我还是背不出FFT的模板我要狗带了
我上面写的什么乱七八糟的,要什么数学,意识流脑补一下就好了。用人话翻译一下:
先看一下这个式子: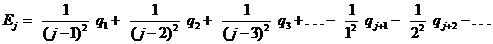 (盗图图源)
(盗图图源)
(当然我的程序里下标是从0开始的,差不多啦)
是不是比写∑什么豁然开朗很多啦!
前半部分是从0开始的,且j-1+1=j,显然卷积搞一下。
后面不是从0开始的,但是实在n-1结束的,我们把所有的q左右颠倒过来,仍然满足和是相等的,然后卷积一下,再倒回来减。
好像依然不是人话,意会一下呗。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<complex> 7 #define pi acos(-1) 8 using namespace std; 9 typedef complex<double> com; 10 typedef long long ll; 11 const int MAXN=270000; 12 double q[MAXN]; 13 com a[MAXN],b[MAXN],c[MAXN],e1[MAXN],e2[MAXN]; 14 int m,n,tmpn,L,Rev[MAXN]; 15 void get_bit(){for (n=1,L=0;n<m;n<<=1) L++;} 16 void get_Rtable(){for (int i=0;i<n;i++) Rev[i]=(Rev[i>>1]>>1)|((i&1)<<(L-1));} 17 void multi(com* a,com* b){for (int i=0;i<n;i++) a[i]*=b[i];} 18 19 20 void FFT(com* a,int flag) 21 { 22 for (int i=0;i<n;i++)if(i<Rev[i])swap(a[i],a[Rev[i]]); //利用逆序表,快速求逆序 23 for (int i=1;i<n;i<<=1) 24 { 25 com wn(cos(2*pi/(i*2)),flag*sin(2*pi/(i*2))); 26 for (int j=0;j<n;j+=(i<<1)) 27 { 28 com w(1,0); 29 for (int k=0;k<i;k++,w*=wn) 30 { 31 com x=a[j+k],y=w*a[j+k+i]; 32 a[j+k]=x+y; 33 a[j+k+i]=x-y; 34 } 35 } 36 } 37 if (flag==-1) for (int i=0;i<n;i++) a[i]/=n; 38 } 39 40 void init() 41 { 42 scanf("%d",&n); 43 tmpn=n; 44 for (int i=0;i<n;i++) scanf("%lf",&q[i]); 45 for (int i=0;i<n;i++) a[i]=(q[i]),c[i]=(q[n-1-i]); 46 for(int i=1;i<n;i++) b[i]=(1.0/i/i); 47 //b仅仅和差有关,还是和下标志一一对应的,不要写成1.0/(i+1)/(i+1) 48 } 49 50 void solve() 51 { 52 m=n<<1;//相乘后的位数是原来的2倍 53 get_bit(); 54 get_Rtable(); 55 FFT(a,1); 56 FFT(b,1); 57 FFT(c,1); 58 multi(a,b); 59 multi(c,b); 60 FFT(a,-1); 61 FFT(c,-1); 62 for (int i=0;i<tmpn;i++) printf("%.3f\n",a[i].real()-c[tmpn-i-1].real());//不要忘了最后还要把c颠倒回来 63 } 64 65 int main() 66 { 67 init(); 68 solve(); 69 }
标签:
原文地址:http://www.cnblogs.com/iiyiyi/p/5720815.html