标签：
背包问题是一个经典的算法问题，可以用动态规划，贪心法，分支界限法等方法解决。问题描述：有n个物品，编号1,2,3，、、n，其中第 i 个物品重量为Wi 价值 Vi ，有一个容量为W的背包。在容量允许范围内，如何选择物品，可以得到最大的价值。（为了简单起见，假设物品的重量 Wi 和价值Vi 都是正数）
今天主要说的是0、1背包问题，解法是动态规划。当然，对于另外两种问题也会有所介绍。
问题分析：
用动态规划解问题首先要有效的找出子问题，可以通过这个子问题得推得原问题的解，通常子问题的实质是和原问题相同的，只是规模上的缩小，也就是说子问题和原问题可以有相同的表示形式，问题可通过不断的缩小规模（一般都会有一个界限）能找到子问题的解。
这个问题要求解的是能用背包带走的物品的最大价值。定义 m[i,w] 为：用第1,、2、3、、i 个物品装入质量<=W的背包的最大价值。
m[i,w]的取值情况分析：
1）
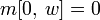，背包的质量为w，里面没有物品，所以它的价值为0；
2）
，背包质量为0，所以里面没法装任何东西， 不论前面的 i 是多少，总价值为0；
对于任意的第 i 个物品，有两种情况，放进背包或者不放。不要第 i 个物品 如果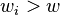
则：
3）
因为第i 个物品的重量大于背包的容量，所以不可放入。
如果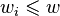
. 那么
4）
对于第 i 个物品，有两种可选择方案：如果放入背包中，那么 m[i,w]=m[i-1,w-wi]+vi。也就是i的前一个的最大值加上自己的价值。如果不要第i个物品，那么：m[i,w]=m[i-1,w]。也就是 i 的前一个的最大值。因为背包问题最后要取得最大的价值，所以就选这两种情况中价值最大的。
在这个问题中，定义子问题： m[i,w] 对于每个子问题，都可通过上面的分析求出。通过3），4）可以发现，每一次求取子问题，问题的规模就被缩小。要么在w 上减小，要么在 i 上减小。最后问题的规模会被缩小为 m[i,0]和m[0,w].而这两个的值都为0，只要逆向思维反推回去，就能逐步得到问题的解。
算法描述
public class Knapsack { static int totalWeight=10;//背包的容量 static int[] w=new int[]{0,2,2,6,5,4};//物品的总重量，其中0号位不使用 static int[] v=new int[]{0,6,3,5,4,6}; static int[] x=new int[w.length]; static int[][] matri=new int[w.length][totalWeight+1]; public static void package0_1(){ for(int j=0;j<=totalWeight;j++){ matri[0][j]=0;//第一行初始为0 } for(int j=1;j<=v.length-1;j++){ matri[j][0]=0;//第一列初始为0 } for (int i=1; i <=w.length-1; i++) { for (int j =1 ; j<=totalWeight; j++) { if(j<w[i]){ matri[i][j]=matri[i-1][j]; }else{ matri[i][j]=Math.max(matri[i-1][j],matri[i-1][j-w[i]]+v[i]); } } } } public static void answer(){ int j=totalWeight; int i; for (i=w.length-1; i>=1;i--) { if(matri[i][j]==matri[i-1][j]){ x[i]=0; }else{ x[i]=1; j-=w[i]; } } x[0]=0; } public static void main(String[] args) { package0_1(); answer(); for (int i = 0; i < x.length; i++) { System.out.println(x[i]); } } }
标签：
原文地址：http://www.cnblogs.com/wxgblogs/p/5721645.html
