标签：

 上部分链接

致谢：因为我的文章之前是在word中写的，贴过来很多用mathtype编辑的公式无法贴过来，之前也没有经验。

参考http://www.cnblogs.com/haore147/p/3629895.html，一文完成公式的迁移。

同时，说一句，word中用mathtype写的公式用ALT+\可以转换成对应的latex语法公式。

5 数据流过滤技术

　　信息大爆炸时代的到来使得针对数据进行深层次的挖掘成为数据处理的核心任务^[21]。但是在上面已经提到了，源数据的来源和数据的组成格式都是各种各样的。想要有效的管理和处理大规模的数据（譬如通信记录、网页访问记录、股票交易记录等等）已经显得尤为必要。在上一节讨论的几种流式数据处理框架已经可以将不同形式的数据进行处理并以统一的形式输出。但是从数据的规模来看并没有缩小，尤其是samza框架。那么对流式数据进行合适的过滤，以降低数据规模，也是值得讨论的问题。

5.1 Bloom Filter

　　流式数据过滤就是按照指定的规则过滤某些数据，过滤主要涉及的是Bloom过滤器以及各种改进形式。下面首先介绍Bloom过滤器。

5.1.1 Bloom Filter原理

　　Bloom^[22]过滤器简单来说就是一个空间效率较高的随机数据结构。它能以特定的数据结构来表示一组序列，以实现成员的查询操作。Bloom Filter允许产生一类错误的反馈（false positive）：即可能存在将不属于这个集合的元素当成这个集合的元素。与相对较低的错误了相比， Bloom Filter以其极大的空间节约率赢得了很多可容忍低误差应用的亲睐。鉴于其特性，很明显Bloom不适用于零误差的场合。Bloom Filter首先是由Burton Bloom在二十世纪七十年代提出的，随后就在数据库的应用中广泛涉及，现在已在其他领域得到更多的关注。

　　下面的例子能更好的解释其工作原理。

　　开始时，我们用Bloom Filter^[22]来表达一个n个元素的集合S={x₁,x₂,x₃, … x_n}，它们是用一组m位的位数组表示，并且均被初始化为0。Bloom Filter使用k个独立的哈希函数，将元素的值映射到另一组数{1,2,3, … ,m}中。为了表示的方便，我们假定，每个被映射的元素通过哈希函数的作用后都映射到{1,2,3, … ,m}范围中。对于S中的每一个元素，通过哈希函数h的作用后所在位h_i(x)被置为1（初始值为0），通常，被作用与哈希函数后就恶能同一个位置会多次映射，从而多次产生“1”，但是仅有第一次做出修改，往后均不修改。为了判断y是否属于集合S，我们检查经过k次哈希运算后的h_k(y)对应的位是否都被置为1。如果满足，则y属于集合S（当然，这其中也不排除上述提到的错误的概率），反之亦然。

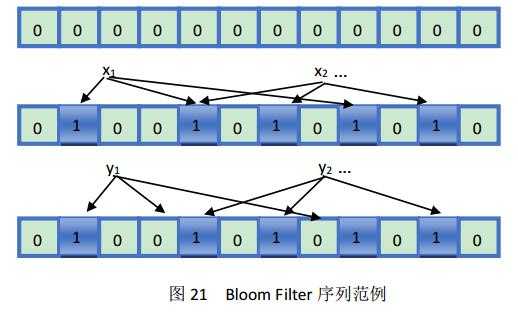
　　图21中，第一行的为初始化的映射表，全部位置被置0，第二行中k=3。而且x₁与x₂有一次映射到了同一个位置。在第三行的映射表中，y₁的某次映射操作指向了0，则说明y₁不是序列中的元素，而y₂是序列中的元素，或者y₂中存在着错误（即上文提到的false positive）。

5.1.2 Bloom Filter错误率

　　上文提到的错误率^[22]，实际上是可以被估计的。这一估计建立在一系列的假设的基础上(1)kn<m (2)选择的k个哈希函数完全随机。在这样的情况下，当把集合S={x₁,x₂,x₃, … x_n}中的所含元素均通过哈希函数映射到m位的数组中后，m位的数组中上一位还是0的概率：

${{p}^{,}}={{(1-\frac{1}{m})}^{kn}}\approx {{e}^{-\frac{kn}{m}}}$

现在记p=${{e}^{-\frac{kn}{m}}}$,很容易看出来p非常的接近p^‘，误差限在O($\frac{1}{m}$),现在将ρ用以表示数组中0的比例，那么其数学期望就是E(ρ)= p^‘。如果ρ已知，则错误率又可以表示为：

${{(1-\rho )}^{k}}\approx {{(1-{{p}^{,}})}^{k}}\approx {{(1-p)}^{k}}$

　　上式中右边的等式已经讨论过了，现在具体谈一下左边的等式的成立情况。等式一成立的条件是经过数学验证后得出的结论，亦即0分布的比率ρ非常集中的分布在数学期望周围。因此得出下面两个公式：

${{f}^{,}}={{\left( 1-{{(1-\frac{1}{m})}^{kn}} \right)}^{k}}={{(1-{{p}^{,}})}^{k}}$和$f={{\left( 1-{{e}^{-\frac{kn}{m}}} \right)}^{k}}={{(1-p)}^{k}}$

　　相比而已，使用近似的值f和p比上面的f^’和p^‘要容易的多。

5.1.3 Bloom Filter位数组界限

　　决定一个Bloom Filter的效率的因素就是映射数组所使用的位元素的个数。即在不超过允许的错误率ε的前提下，该使用多少位（m）来表示集合中n个元素的映射结果。

假设^[22]我们的子集合大小是u。我们必须为每一种可能的集合$\left( \begin{matrix}u  \\n\\\end{matrix} \right)$必须提供一个m位的串。对于每一个集合X，F(X)表示其位数组。那么对于x∈X，如果存在查询结果S=F(X)，则S接受x，否则S拒绝x。

　　下面考虑特定的一个包含n的元素的源数据集合X。任何用以表示x∈X的每一个位元素必须包含x的全体。但是因为存在错误率的原因，也允许接受ε（u-n）个其他的元素。综上，每个S均可以接受n+ε（u-n）个元素。因此，一个特定的数组可以表示$\left( \begin{matrix}n+\varepsilon (u-n) \\n \\\end{matrix} \right)$个子集。当我们使用大小为m的位元素来表示，则产生了2^m个不同的子串用以表示n大小的数据集合的映射解。所以有如下不等式：

${{2}^{m}}\left( \begin{matrix}n+\varepsilon (u-n)  \\n  \\\end{matrix} \right)\ge\left( \begin{matrix}u  \\n  \\\end{matrix} \right)$

　　或者可以表示成如下的形式：

$m\ge {{\log }_{2}}\frac{\left( \begin{matrix}u  \\n  \\\end{matrix}\right)}{\left( \frac{n+\varepsilon (u-n)}{n} \right)}\approx{{\log }_{2}}\frac{\left( \begin{matrix}u  \\n  \\\end{matrix}\right)}{\left( \frac{\varepsilon u}{n} \right)}\ge{{\log }_{2}}{{\varepsilon }^{-n}}=n{{\log }_{2}}(\frac{1}{\varepsilon })$

　　5.1.3节给出的各式都是基于一个原则，即n远小于εu。这也是根据实验经验得出的结论。我们因此也得出一个结论，在存在错误的情况下，m至少要等与nlog₂（1/ε）才能满足要求。

5.1.4 Bloom Filter Hash最优个数

　　假设如下的情况：如果我们限定了n和m，那么如何选择哈希函数的个数k，从而达到过滤效果最优^[22]的情况呢？现在有两种考虑：如果提供较多的哈希函数供映射，那么如果不在x中的元素映射后会有很大的概率得到结果0。如果选择较少的哈希函数，那个位数组中的0元素也会大大增加。因此要考虑一种折中。哈希函数个数的最优情况可以通过对f和k求导得出。

　　记f=exp（kln(1-e^-kn/m)）,g=kln(1-e^-kn/m)。显然，当g取到最小的时候，f自然也是达到最小值。

$\frac{\partial g}{\partial k}=\ln \left( 1-{{e}^{-\frac{kn}{m}}}\right)+\frac{kn}{m}\frac{{{e}^{-\frac{kn}{m}}}}{1-{{e}^{-\frac{kn}{m}}}}$

　　当k=ln2（m/n）时候，g取到最小值。此时f=(0.5)^k≈(0.6185)^m/n，g与g^’的表达式下面直接给出：

$g=-\frac{m}{n}\ln (p)\ln (1-p)$和${{g}^{‘}}=\frac{1}{n\ln (1-\frac{1}{m})}\ln ({{p}^{‘}})\ln (1-{{p}^{‘}})$

5.2 Compressed Bloom Filters

　　Compressed Bloom Fiilters是基于Bloom Filter的改进形式，既继承了Bloom Filter的优点，又针对其不足^[23]，在执行效率和性能方面做了提升，下面将从原理和实验结果等方面进行对比，很多与Bloom Filter相似之处仅一带而过。

5.2.1 Compressed Bloom Filters提出

　　5.1节也提到了，Bloom Filter虽然会产生映射阶段的错误，但是错误的概率因为不是很大，鉴于其能带来的空间效率的节省，仍然备受关注。但是这一过滤器仍存在一部分问题。

　　譬如在传递消息时，Bloom Filter的大小就受到了严格的限制：在共享网络缓存信息时，就有学者提出使用Bloom Filter作为对应的过滤器。实际上，代理并不是传输缓存信息以达到共享的目的，取而代之的则是在过滤器间进行广播通信。这一效率对于原有的Bloom Filter效率比较低。通过Compressed Bloom Filters的提出，明显减少了广播的次数、错误率、计算和查询次数。

5.2.2 Compressed Bloom Filters原理

　　我们上面提到的关于哈希函数的k值的最优解是基于一个假设，即：我们设计m与n的关系时就是为了最大可能的降低错误率。当我们认为Bloom Filter常驻内存时，这个假设没有错。但是^[25]在网络缓存应用中，过滤器不可能常驻内存，它还要在代理间传输信息。这个我们一个提示：我们也许不一定要调整n和m的参数，也许可以对传输的数据进行压缩。因此我们选择在压缩后，来处理错误率的问题。

　　现在考虑Bloom Filter，最佳的k=ln2*(m/n),换一个说法就是,p=1/2，即当错误率最低时候，元数组里面的0的个数占一半。这种情况下貌似不能进行压缩。然而Bloom Filter分析思路没有把压缩的情形考虑在内，而是把Bloom Filter看作常驻内存的数据结构，讨论出位数组大小固定的情况下求哈希函数个数的最优值。

　　与前述Bloom Filter对比。Compressed Bloom Filter^[25]提出了4个性能参数：除了计算时间（对应于哈希函数的个数k）、错误率f，还有另外的两种度量：未经压缩的过滤大小（可以后续使用m来度量）以及压缩后传输数据的大小z。现在讨论一种情况：在某种情形下，压缩后位数组z的大小比原始未压缩过滤数据大小m重要的多，给定z、n求最优k和m。

　　我们单独来看位数组中的每一位。首先假设我们有最佳的压缩算法。即有原来m位的元数组可以被压缩成z=H(p)大小。H(p)=-plog₂p-(1-p)log₂(1-p)。压缩函数使用H(p)产生的平均值作为元数组的初始串。得到这时候的f（左边），并带入m，得到新的f（右边）

$f={{(1-p)}^{k}}={{(1-p)}^{(-\ln p)(\frac{m}{n})}}$和改进的$f={{(1-p)}^{-\frac{z\ln p}{nH(P)}}}$

　　由于在此处z、n固定，且z≥n，可以求的最小的β。

$\begin{align}& \beta ={{(1-p)}^{-\left( \frac{\ln p}{H(P)} \right)}}={{e}^{-\left( \frac{\ln p*\ln(1-p)}{H(p)} \right)}} \\& =\exp \left( \frac{-\ln p*\ln (1-p)}{(-{{\log }_{2}}e)(p\ln p+(1-p)\ln(1-p))} \right) \\\end{align}$

　　此处求β的最大值，等同于求γ的最大值（对其求导）。

$\gamma =\left( \frac{p}{\ln (1-p)}+\frac{1-p}{\ln p} \right)$

$\frac{d\gamma }{dp}=\frac{1}{\ln (1-p)}-\frac{1}{\ln p}+\frac{p}{(1-p)*{{\ln }^{2}}(1-p)}-\frac{1-p}{p{{\ln }^{2}}(p)}$

　　p = 1/2时γ取得最小值，即β和f取得最大值。当p = 1/2，即k = (ln2) (m/n)时，在不考虑压缩的情况下错误率最低，而在考虑压缩的情况下错误率反而最高。换句话说，压缩总是能够降低错误率。

 5.2.3 改进效果对比

　　下面^[24]通过测试一批具体的数据来判断是否compressed bloom filter能够提升处理的性能。例子中分别采用了8和16位的元数组。同样值得注意的是，在每一组的对比Bloom Filter中f的参数都是给出的。例如在网络缓存共享应用中，由于Bloom Filter的更新导致本地缓存内容的改变同样也会引发另外的错误率。对于compressed Bloom Filter在测试的过程中采用了仿真的方法。我们重复实验大概1000次。创建了n=10000的数据以及m=140000位。图22和图23说明了测试的结果。

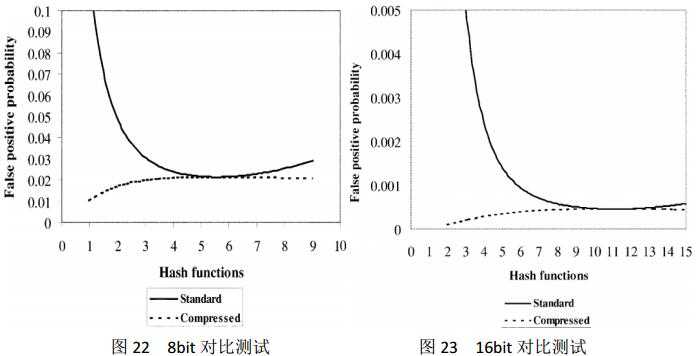
　　图22和图23的测试结果值得关注。如果Bloom filter常驻的内存是在使用中必须要考虑的一个问题或者说是性能瓶颈的话，那么最好不要保持Bloom filter的现存形式。同样的改进的Compressed Bloom Filter也能够带来较好的性能和较低的错误率。

5.3 其他过滤方式

　　受篇幅所限，此处对于其他的过滤算法不再详细展开。仅概要地做一番讨论。下面讨论Partial Bloom Filter、Counting Bloom Filter、Spectral Count Filter、Dynamic Bloom Filter等。

5.3.1 Partial Bloom Filter

　　再来回顾一下Bloom Filter，它是有k个哈希函数构成，通过哈希将源集合中的源数据映射到长度为m的位数组中。每个哈希函数映射的范围都是相同的，因此存在多个源数据映射到同一位置。而Prttial Bloom Filter中，则改变了这一思路。元数组被分割成了k个区域，则对于每个哈希函数来说，都将映射到不同的区域中。虽然通过哈希操作得到的映射值相同，但是却互不干扰。对于错误率来说，两者比较接近，但是还是稍微弱于标准的Bloom Filter。

${{\left( 1-\frac{k}{m} \right)}^{n}}\le {{\left( 1-\frac{1}{m} \right)}^{kn}}$

　　但是实际中因为独立了映射的范围，使得对数则的访问可以并发，从而提高了执行的效率。

5.3.2 Counting Bloom Filter

　　标准Bloom Filter适合静态集合，因为Bloom Filter的一大特性是支持插入和查找，但是如果要表达的集合并不是静态的，或者说随着应用的需求在不断的变化，那么Bloom Filter就显得有点力不从心。 Counting Bloom Filter的正好是弥补了这个问题，它将标准Bloom Filter位数组的每一位（m）扩展为一个独立的计数器counter^[25]，在插入元素时给对应的k个Counter的值分别加1，删除元素时给对应的k个Counter的值分别减1。Counting Bloom Filter给Bloom Filter增加了删除操作，前提是必须付出较多的存储空间。图24展示了其删除操作的过程。

5.3.3 Spectral Bloom Filter

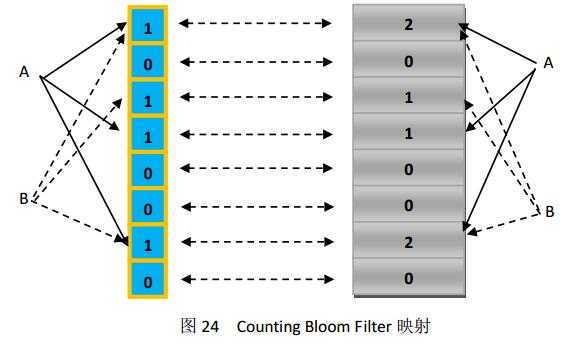
　　基本的Bloom filter通过哈希函数将元素映射到位数组中，该位为1则表示元素在其中。上面提到的Counting bloom filter改进了Bloom filter，扩展了删除操作。一旦位扩展成了一个小型的计数器，每一个counter还能表示映射的个数。类似的，扩展能存储更多的细节信息。Spectral Bloom Filter（SBF）就是基于此提出来的。BF和CBF仅仅实现了判断一个元素是否属于某个集合。SCF则将其与集合元素的出现次数关联。

5.3.4 Dynamic Count Filter

　　5.3.3节介绍的SBF在CBF的基础上增加了频度的概念，使得这一过滤器可以被部署到多元的应用中。但是，SBF在增加了功能的同时大大滞后了处理的效率。Dynamic count filter在上述模型的基础上进一步改进。DCF和SBF的不同之处，也就是counter的存储结构^[26]。图25给出DCF的存储结构，具体信息可参照^[26]。

5.3.5 CBF、SBF、DCF比较

　　表5给出了三种改进的Bloom Filter过滤在多个性能指标下的比较^[26]。

表5  CBF、SBF、DCF性能比较

6 数据流挖掘应用（以股市趋势预测为例）

　　数据挖掘就是从海量的数据中通过各种工具的运用结合各种算法和框架，找到数据内在的联系。从而为进一步决策提供参考和分析意见。比较著名的案例就是“啤酒与尿布”。然而如今，数据挖掘已经深入各行各业，涉及各个领域。下面就以一个对股票市场价格预测方法和实施过程进行分析说明和总结。

6.1 研究背景

股票市场^[27]瞬息万变，因此对于股市的预测在现代金融市场显得尤为重要。传统的预测方法是基于股票票面价格进行的数据挖掘。然而，股票的价格受很多因素的干扰。对于受干扰的数据源，用以预测的随机波动模型显得效率比较低下。干扰源通常来自两个方面：内幕交易和市场操控。上述的异常现象将会对股市市值的预测产生很大的影响。因此我们也将借助于此来最大程度的降低这种干扰因素对股票价格预测的影响。在研究中我们将限定于上升阶段的预测，因为该阶段代表着着稳定和长期利好。在我们的研究中，我们将要探测所有的异常，并且标记在价格序列中，然后当我们的方法检测到异常后就能很快的做出股市价格显著变化的预测。例如在下图中，在价格曲线上异常的部分被标记成“+”，x轴代表的是交易量而y轴（竖轴）代表的是股价。

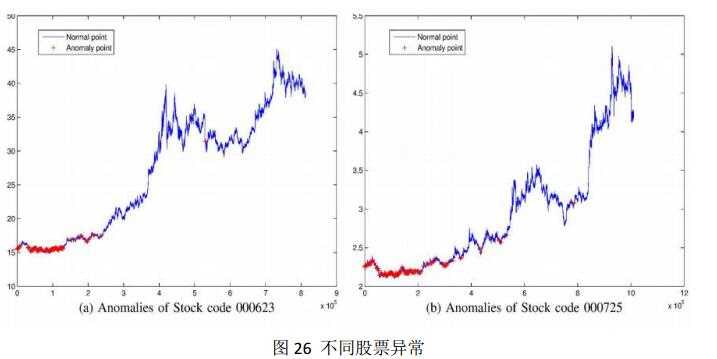
　　从图26我们可以很清晰的看到，在异常标记后的那一段中，有一个明显上扬的趋势，下一节我们将要详细的介绍具体的实施步骤。

6.2 处理方法

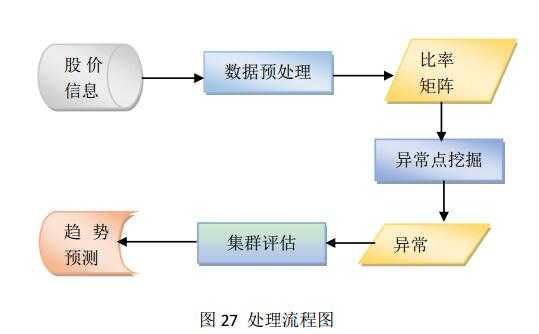
　　图27详细展示了我们处理的步骤。我们首先在数据源中获得数据，然后进行预处理。接着将高频数据放入比率矩阵通过算法找出异常。根据异常的位置和结果，最终可以得出一些预测信息。

6.2.1 数据预处理

　　研究中采用的数据都是高频的逐笔交易的数据。逐笔交易的数据在是一种金融行业使用的规格化的数据。这类数据记录着股票交易所内每笔股票的交易。如果某一股票有1000条记录，那么当天必须产生1000条交易信息。这样的数据规模是相当庞大的。没条记录按如下形式定义：

R={t,p,c,v,a,b}

　　这些数据^[27]分别代表着如下的含义，t：交易时间，p：交易价格，c：交易差价，v：交易级别，a：交易数量，b：买入或者卖出的标记位。表6记录了一段时间内的交易数目。

表6  交易记录表

         获得数据后就开始预处理的步骤了，步骤如下：

（1）准备逐笔交易记录：

对于每一代码的股票，统计当天的进入交易矩阵T的数量。T矩阵的每一行都是我们刚刚定义的R格式信息。

（2）统计所有股价

（3）统计某一股票代码的股价

我们从矩阵T中定义一种新的向量格式T_S^V(P)。其中v代表矩阵中的列，s代表特定的股票，p表示特定的价格。汇总所有的股票信息构成T^V(P)。

（4）汇总比率矩阵

　　对上上面获得的列向量T_S^V(P)和T^V(P)，要设法缩减规模。因为规模太大后，出现次数较少的就会被当成异常的情况来处理。在这里，我们定义其上限为1000。并且定义一种新的价格向量。P={unique prices}。则有:

$M_{si}^{v}=\frac{N\left( T_{S}^{V}\left( {{P}_{i}} \right) \right)}{N\left( T_{S}^{(V<1000)}\left( {{P}_{i}} \right) \right)}$和$M_{i}^{v}=\frac{N\left( T_{{}}^{V}\left( {{P}_{i}} \right) \right)}{N\left( T_{{}}^{(V<1000)}\left( {{P}_{i}} \right) \right)}$ 

　　其中i代表行号，v代表列号。N是一个计数函数，用来计算vector的大小。M_SI^V是某个具体股票的矩阵，而M^v则是全体股票的矩阵。产生的矩阵如下：

6.2.2 算法

　　这两个算法^[27]的作用分别是用来检测数据中的异常数据，检测出异常点的价格和数量，以及用来定位异常数据在矩阵中的位置。

6.3 研究成果

6.3.1 集群

　　在这一部分我们采用了k-均值聚类算法（k-means clustering algorithm）来判断是否有集群的存在。实验结果见图28。

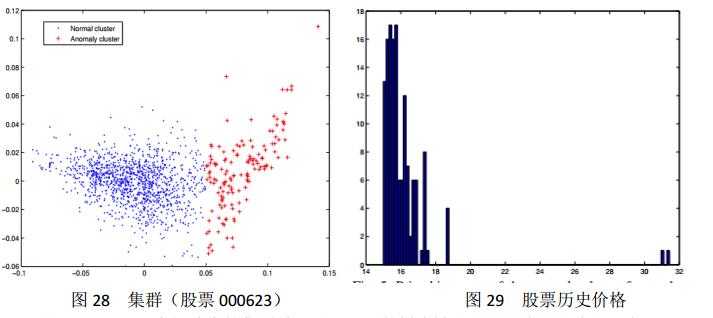
　　图28显示了比率矩阵中的集群效果图，里面的样本被分成了两类，一类用”.”表示，一类用”+”表示。左边的蓝色区域表示的是正常的数据，右边表示的是异常的交易数据。这表明了我们的算法与传统的集群算法是一致的，没有冲突。而且我们的算法更高效，因为可以从图28和29中读取到我们需要的一切信息。

6.3.2 结果预测

　　实验^[27]中随机选取了深交所的200支股票。发现111支存在着异常的集群现象，如图28和图29所示。我们分析了100内的数据，采样结果如图30。我们很容易看到其中上扬的趋势。在这里我们定义成功率（成功样本/总体样本），成功率的示意图为图31。

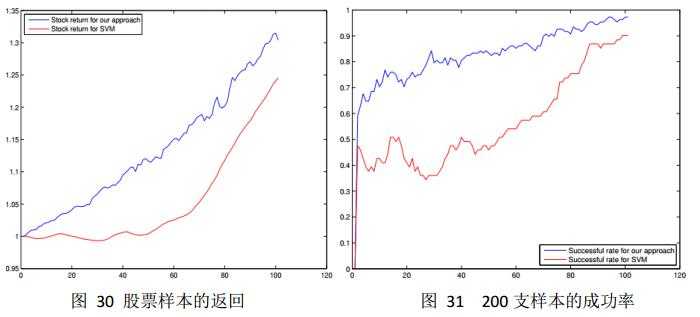
　　从图31看，实验得出的成功率是在可控范围内的，也达到了对应的预测效果。因此符合预期所设定的实验结论。

7 在撰写调研报告中发现的不足

7.1 未提到的内容

　　受篇幅所限，很多关于数据流挖掘的相关技术知识没有提到，而这些知识又是在流式数据挖掘过程中必不可少的。例如：

　　流数据模型：现在通用的流数据模型主要分为三种，分别是滑动窗口模型(sliding window model)、界标模型(landmark model)和快照窗口模型(snapshot window model)。

　　流抽样技术：抽样过程中方法的选取问题。不同的方法在计算频率时很可能使得抽样得出的结果与全局的频率差距很大。

　　对独立元素的统计问题：如何统计？其中一种可选的方法是把当前所有元素列表保存在内存中，使用hash和搜索树进行数据的保存和检索。但是这也会遇到问题。如果内存容纳不了如此多的元素怎么处理？

　　其他诸如矩估计等问题也没有在正文中具体讨论。

7.2 发现的问题

　　我在写调研报告的过程对比了很多的新技术，通过最新的文献和会议资料的阅读拓宽了对大数据尤其是流式数据分析的理解。同时也在思考这些技术背后是不是无懈可击，有没有可以改进或者值得其他人进一步分析的方面。这里列出在调研流式数据相关应用方面的所发现的一个问题。即流式数据的获取和隐私的保护。拿上面的股票预测案例来说，实验的第一步是数据的预处理，预处理的前提是数据的获取，但是很显然，这类数据不是那么轻易可以获取到的，而且在实验中需要获取的是“逐笔交易”记录，更加的隐蔽。比如利用大数据在医院等场所进行某类疾病的预测时候，也会遇到同样的问题，对于病人的信息，以及第7节提到的股票交易信息，都是无形的财富，无法说立即获取，牵涉到各方的利益。再者说，如果获取了，如何保证信息的不泄漏，无论是个人的股票交易记录还是病人的信息都是十分隐私的信息。即便是在操作中对某些字段采用模糊化也不能保证根据数据之间的关联性推测出一些相对隐私的信息，这些都是流式数据处理中要注意的地方。

参考文献

[1]       Vibha Bhardwaj, Rahul Johari. Big Data Analysis:Issues and Challenges. Electrical, Electronics, Signals, Communication and Optimization (EESCO), 2015 International Conference. Jan 2015.

[2]       Marcos D. Assunção, Rodrigo N. Calheiros, Silvia Bianchi, Marco A.S. Netto, Rajkumar Buyya. Big Data computing and clouds: Trends and future directions. J. Parallel Distrib. Comput. 79–80 Mar 2015.

[3]       Aaron N. Richter, Taghi M. Khoshgoftaar, Sara Landset, Tawfiq Hasanin. A Multi-Dimensional Comparison of Toolkits for Machine Learning with Big Data. Information Reuse and Integration (IRI), 2015 IEEE International Conference. Aug 2015.

[4]       Shabia Shabir Khan, M.A.Peer, S.M.K.Quadri. Comparative Study of Streaming Data Mining Techniques. Computing for Sustainable Global Development (INDIACom), 2014 International Conference. Mar 2014.

[5]       Gianmarco De Francisci Morales, Albert Bifet. SAMOA: Scalable Advanced Massive Online Analysis. Journal of Machine Learning Research(16) 149-153, 2015.

[6]       “samoa,” http://samoa.incubator.apache.org/.

[7]       徐加文. 开源数据流挖掘框架学习.电子科技大学. 2014.

[8]       Jan Sipke van der Veen, Bram van der Waaij, Elena Lazovik, Wilco Wijbrandi, Robert J. Meijer. Dynamically Scaling Apache Storm for the Analysis of Streaming Data. Big Data Computing Service and Applications (BigDataService), 2015 IEEE First International Conference. Mar 2015.

[9]       “storm 简介,”http://www.aiuxian.com/article/p-102353.html.

[10]   “storm,” http://storm.apache.org/index.html.

[11]   “spark,” http://spark.apache.org/index.html.

[12]   Tony Sicilian. Streaming Big Data: Storm, Spark and Samza. Enterprise Java. Feb 2015.

[13]   “dataframe,” http://spark.apache.org/docs/latest/sql-programming-guide.html#dataframes.

[14]   夏俊鸾, 邵赛赛. Spark Streaming：大规模流式数据处理的新贵.CSDN程序员. 2014年.

[15]   Matei Zaharia, Mosharaf Chowdhury, Tathagata Das, Ankur Dave, Justin Ma, Murphy McCauley, Michael Franklin, Scott Shenker, Ion Stoica. Resilient Distributed Datasets: A Fault-Tolerant Abstraction for In-Memory Cluster Computing. Technical Report No. UCB/EECS-2011-82. July 2011.

[16]   Lei Gu, Huan Li. Memory or Time: Performance Evaluation for Iterative Operation on Hadoop and Spark. High Performance Computing and Communications & 2013 IEEE International Conference on Embedded and Ubiquitous Computing (HPCC_EUC), 2013 IEEE 10th International Conference. Nov 2013.

[17]   “samza,” http://samza.apache.org/.

[18]   “flink,” http://flink.apache.org/features.html#unified-stream-amp-batch-processing.

[19]   “StreamBase,”http://www.tibco.com/products/event-processing/complex-event-processing/streambase-complex-event-processing/?capabilities.

[20]   Fatos Xhafa, Victor Naranjo, Santi Caballe, Leonard Barolli. A Software Chain Approach to Big Data Stream Processing and Analytics. Complex, Intelligent, and Software Intensive Systems (CISIS), 2015 Ninth International Conference. July 2015.

[21]   Sourav Dutta, Souvik Bhattacherjee, Ankur Narang. Towards “Intelligent Compression” in Streams: A Biased Reservoir Sampling based Bloom Filter Approach. EDBT/ICDT 2012 Joint Conference. Mar 2012.

[22]   Andrei Broder, Michael Mitzenmacher. Network Applications of Bloom Filters: A Survey. Internet Mathematics(4) 485-509.

[23]   Paul Hurley, Marcel Waldvogel. Bloom Filters: One Size Fits All? Local Computer Networks, 2007. LCN 2007. 32nd IEEE Conference. Oct 2007.

[24]   Michael Mitzenmacher. Compressed Bloom Filters. Networking, IEEE/ACM Transactions. 604-612,2002.

[25]   “Counting Bloom Filter,” http://blog.csdn.net/jiaomeng/article/details/1498283.

[26]   J. Aguilar-Saborit, P. Trancoso, V. Muntes-Mulero. Dynamic Count Filters. SIGMOD Record. Mar 2006.

[27]   Zhao Lei, Wang Lin. Price Trend Prediction of Stock Market Using Outlier Data Mining Algorithm. Big Data and Cloud Computing (BDCloud), 2015 IEEE Fifth International Conference. Aug 2015.

提升大数据数据分析性能的方法及技术（二）

标签：

原文地址：http://www.cnblogs.com/csbdong/p/5721573.html