标签:
这是剑指offer中关于二叉树重构的一道题。题目原型为:
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
一、二叉树的数据结构
做题之前,我们先熟悉下二叉树的数据结构。其一,定义:二叉树是一个连通的无环图,并且每一个顶点的度不大于3。有根二叉树还要满足根结点的度不大于2。有了根结点之后,每个顶点定义了唯一的父结点,和最多2个子结点。然而,没有足够的信息来区分左结点和右结点。如果不考虑连通性,允许图中有多个连通分量,这样的结构叫做森林。(定义来自百度百科)
由定义可知,二叉树含有许多节点,而不同节点之间通过子父关系来连接。一般来说,二叉树的节点由结构体来定义,如下所示:
1 struct TreeNode {
2 int val;
3 TreeNode *left;
4 TreeNode *right;
5 TreeNode(int x) : val(x), left(NULL), right(NULL) {}
6 ~TreeNode() {
7 cout << "TreeNode with value " << val << " has been destroyed." <<endl;
8 }
9 };
该结构体定义了节点的int型变量(当然也可以是其它类型),以及指向左右孩子的指针。在TreeNode中,我们还定义了构造函数和析构函数,其实可有可无,对本题来说没有多大意义。
二、二叉树的建立
二叉树的建立过程,就是不断扩展节点的过程。建立根节点,由根节点建立左右子节点,再递归的建立子节点的子节点。我们下面看看代码的实现过程:
1 void BiTree::createBiTree(struct TreeNode* &root) {
2 int val;
3 //cout << "Please input the tree node:" << endl;
4 cin >> val;
5 if (999 == val) {
6 root = NULL;
7 }
8 else {
9 //root = (struct TreeNode*) malloc(sizeof(TreeNode));
10 root = new TreeNode(1);
11 if (root == NULL)
12 return;
13 root->val = val;
14
15 cout << "Please input the left child of " << val << ": ";
16 createBiTree(root->left);
17
18 cout << "Please input the right child of" << val << ": ";
19 createBiTree(root->right);
20 }
21 }
这里,我是把创建二叉树的方法createBiTree()作为了BiTree的成员函数(简单说明一下)。
1、首先,我们看参数 struct TreeNode* &root, 这是结构体指针的引用。为什么要传递引用呢,就是希望函数体外的指针变量能指向函数体内所新建的根节点。若只是指针传递,那么函数体内新建的节点和函数体外的指针变量是没有指向关系的。
2、然后就是新建节点,
//root = (struct TreeNode*) malloc(sizeof(TreeNode));
root = new TreeNode(1);
这两条语句的效果相同。如果创建成功,那么递归调用本方法,创建后续节点。
三、二叉树的遍历
二叉树有三种遍历方法:先序,中序,后序。即父前(父-左-右),父中(左-父-右),父后(左-右-父)。
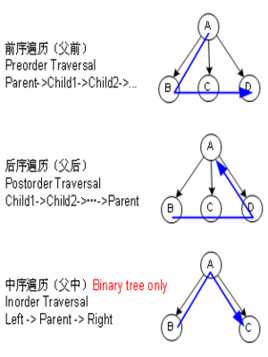
1、先序遍历
1 // 这里参数传递指针,或指针的引用都可以
2 void BiTree::preOrder(struct TreeNode* &root) {
3 if (root == NULL)
4 return;
5 cout << root->val << ‘ ‘;
6 preTrav.push_back(root->val);
7 preOrder(root->left);
8 preOrder(root->right);
9 }
其中,preTraa.push_back(root->val);我只是把先序遍历的结果存在了vector 中,方便重构二叉树时作为输入。下同。
2,、中序遍历
1 void BiTree::inOrder(struct TreeNode* root) {
2 if (root == NULL)
3 return;
4 inOrder(root->left);
5 cout << root->val << ‘ ‘;
6 inTrav.push_back(root->val);
7 inOrder(root->right);
8 }
3、后序遍历,就不贴代码了。
另外,值得说明一下的是。这里的遍历方法都是通过递归来实现的,还有遍历的非递归算法(日后再详细去探讨,这里先着重看这个题目,也不知日后是否会想起这个任务。。。囧)
三、已知先序遍历,中序遍历,重构二叉树
我们观察先序遍历和中序遍历的结果。先序遍历的第一个节点肯定是根节点,然后在中序遍历中找到此根节点,我们可以看到,中序遍历中根节点以左是二叉树的左子树,根节点以右是二叉树的右子树。然后,左右子女树又可以单独的看成一个独立的二叉树,然后再对其划分,如此递归,便可重构二叉树的结构。下面上代码:
1 struct TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> in){
2 //TreeNode* head = new TreeNode(pre[0]);
3 /* 注意上面这一条语句不能放在函数体的第一句。
4 * 因为此时还不能确定pre这个vector是否为空,如果不为空,那么访问pre[0]就是非法内存访问。此时若debug,会有
5 * Program received signal SIGSEGV, Segmentation fault.的错误信息。其中,SIG是signal的缩写,SEGV是segmentation violation(段违例)的缩写。详见维基百科
6 * 所以,此条语句放在return NULL;语句之后为宜,因为这个时候已经确定vector in不为空。但是好像没判断pre是否为空呢,这就可以了??
7 */
8 vector<int> left_pre, left_in, right_pre, right_in;
9
10 int pos = 0;
11 int length = in.size();
12
13 if (length == 0)
14 return NULL;
15
16 TreeNode* head = new TreeNode(pre[0]);
17
18 for (int i = 0; i < length; ++i) {
19 if (pre[0] == in[i]) {
20 pos = i;
21 break;
22 }
23 }
24
25 for (int i = 1; i < pos + 1; ++i) {
26 left_pre.push_back(pre[i]);
27 left_in.push_back(in[i-1]);
28 }
29
30 for (int i = pos + 1; i < length; ++i) {
31 right_pre.push_back(pre[i]);
32 right_in.push_back(in[i]);
33 }
34
35 head->left = reConstructBinaryTree(left_pre, left_in);
36 head->right = reConstructBinaryTree(right_pre, right_in);
37
38 return head;
39
40 }
其实,关于这个重构函数,笔者还有一个问题,就如函数中注释中所诉。还请广大博友解答下(新手博客,都没人看,好忧伤~_~!)
四、重构验证
首先,贴上验证程序。验证程序综合了上述建立二叉树,遍历二叉树以及重构二叉树的相关实现。
 View Code
View Code下面我们看看程序结果。
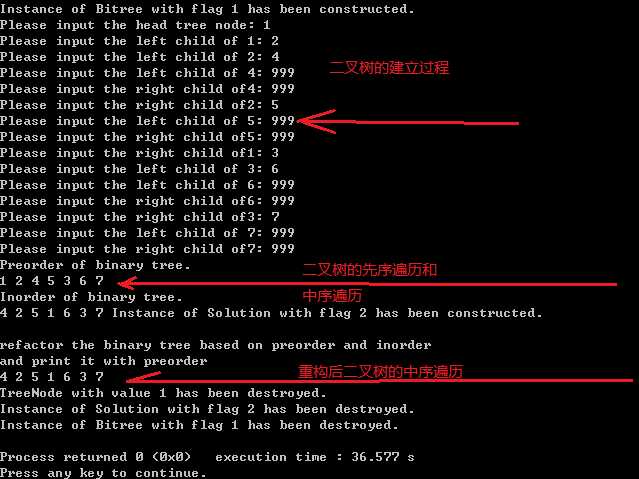
从结果中我们可以看见,重构后二叉树的中序遍历和我们输入的二叉树的中序遍历相同。我们还可以输出重构后的先序遍历,来确定我们的重构是正确的。
二叉树的重构暂且先探讨这。二叉树还有其它很多特性需要没我们去研究,择日再说。
标签:
原文地址:http://www.cnblogs.com/Leo_wl/p/5721893.html