标签：

1010 Rower Bo

首先这个题微分方程强解显然是可以的，但是可以发现如果设参比较巧妙就能得到很方便的做法。

先分解v_1v?1??，

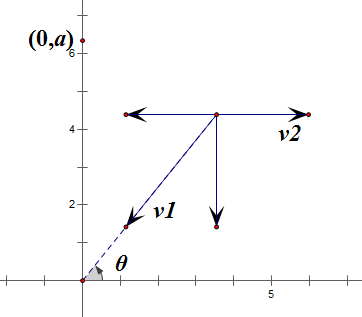
设船到原点的距离是rr，容易列出方程

\frac{ dr}{ dt}=v_2\cos \theta-v_1?dt??dr??=v?2??cosθ−v?1??

\frac{ dx}{ dt}=v_2-v_1\cos \theta?dt??dx??=v?2??−v?1??cosθ

上下界都是清晰的，定积分一下：

0-a=v_2\int_0^T\cos\theta{ d}t-v_1T0−a=v?2??∫?0?T??cosθdt−v?1??T

0-0=v_2T-v_1\int_0^T\cos\theta{ d}t0−0=v?2??T−v?1??∫?0?T??cosθdt

直接把第一个式子代到第二个里面

v_2T=\frac{v_1}{v_2}(-a+v_1T)v?2??T=?v?2????v?1????(−a+v?1??T)

T=\frac{v_1a}{{v_1}^2-{v_2}^2}T=?v?1???2??−v?2???2????v?1??a??

这样就很Simple地解完了，到达不了的情况就是v_1< v_2v?1??<v?2??（或者a>0a>0且v_1=v_2v?1??=v?2??）。

1011 Teacher Bo

考虑一种暴力,每次枚举两两点对之间的曼哈顿距离,并开一个桶记录每种距离是否出现过,如果某次枚举出现了以前出现的距离就输 YESYES ,否则就输 NONO .

注意到曼哈顿距离只有 O(M)O(M) 种,根据鸽笼原理,上面的算法在 O(M)O(M) 步之内一定会停止.所以是可以过得.

一组数据的时间复杂度 O(\min{N^2,M})O(min{N?2??,M}) .

Rower Bo

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1248    Accepted Submission(s): 474
Special Judge

#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
int main()
{
    int a,v1,v2;
    while(~scanf("%d%d%d",&a,&v1,&v2))
    {
        if(a==0) {printf("0.000\n");continue;}
        if(v1<=v2)
        {
            printf("Infinity\n");
        }
        else
        {
            double v=(v1*v1-v2*v2)+0.0;

            double ans=(a*v1*1.0)/v;
            printf("%.12lf\n",ans);
        }
    }
    return 0;
}

View Code

 

hdu 5761 Rowe Bo 微分方程

标签：

原文地址：http://www.cnblogs.com/superxuezhazha/p/5725033.html