标签：
1. 线性规划的概念
线性规划是研究在一组线性不等式或等式约束下使得某一线性目标函数取最大（或最小）的极值问题。
2. 线性规划的标准形
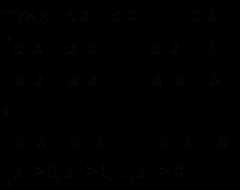
特点：目标函数求极大；等式约束；变量非负。
令
则线性规划标准形的矩阵表达式为：
约定：
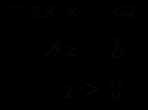
如何化标准形：
（I） 目标函数实现极大化，即
，令
，则
；
（II）约束条件为不等式
约束条件为“
” 不等式，则在约束条件的左端加上一个非负的松弛变量；
约束条件为“
” 不等式，则在约束条件的左端减去一个非负的松弛变量。
（III）若存在无约束的变量
，可令
，其中
3. 单纯形法求解
（I） 化为标准形（要求
），确定初始基
，建立初始单纯形表（假设A矩阵中存在单位矩阵）；
（II）若
，则已得到最优解，停止。否则转入下一步；
（III）若在
中，存在
，而
，则无最优解，停止。否则转入下一步；
（IV）由
，确定
为换入变量，按
规则
可确定
为换出变量；
（V）以
为主元进行迭代
即将
迭代成
，
并将单纯形表
列中的
换成
，得到新的单纯形表；
重复（ⅱ）~（ⅴ）。
4. 单纯形法求解例示
|
两阶段法
第一阶段，求初始基可行解：在原线性规划问题中加入人工变量，使约束矩阵出现单位子矩阵，然后以这些人工变量之和W求最小为目标函数，构造如下模型：
 |
对上述模型求解（单纯形法），若W=0，说明问题存在基本可行解，可以进行第二个阶段；否则，原问题无可行解，停止运算。
第二阶段：在第一阶段的最终表中，去掉人工变量，将目标函数的系数换成原问题的目标函数系数，作为第二阶段计算的初始表（用单纯形法计算）。
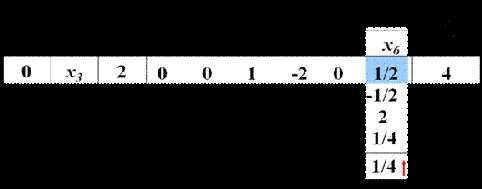
例：
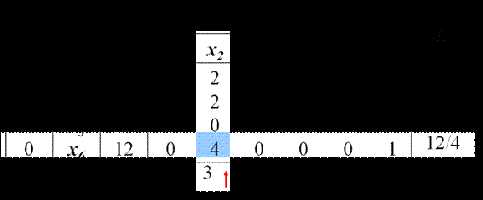
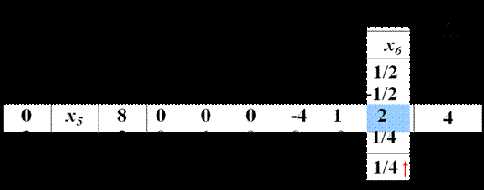
第一阶段
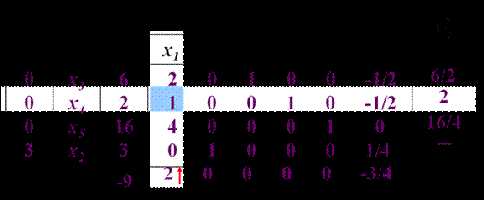
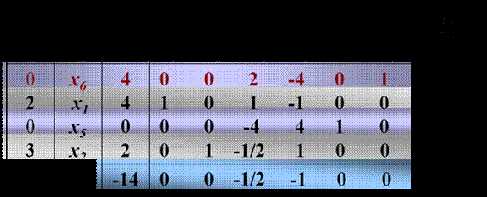
第二阶段
∴最优解为（4 1 9 0 0），目标函数 Z = –2
退化： 即计算出的θ（用于确定换出变量）存在有两个以上相同的最小比值，会造成下一次迭代中由一个或几个基变量等于零，这就是退化（会产生退化解）。
虽任意换出变量，目标函数值不变，但此时不同的基却表示为同一顶点，其特例是永远达不到最优解。需作如下处理：
⑴. .当
中出现两个以上最大值时，选下标最小的非基变量为换入变量；
⑵.当θ中出现两个以上最小值时，选下标最小的基变量为换出变量。
参考文献：
[1] 《运筹学》教材编写组. 运筹学. 北京: 清华大学出版社.
标签：
原文地址：http://www.cnblogs.com/lotusto/p/5726954.html
