标签:
堆的定义
堆(heap),这里所说的堆是数据结构中的堆,而不是内存模型中的堆。堆通常是一个可以被看做一棵树,它满足下列性质:
[
性质一
] 堆中任意节点的值总是不大于(不小于)其子节点的值;
[
性质二
] 堆总是一棵完全树。
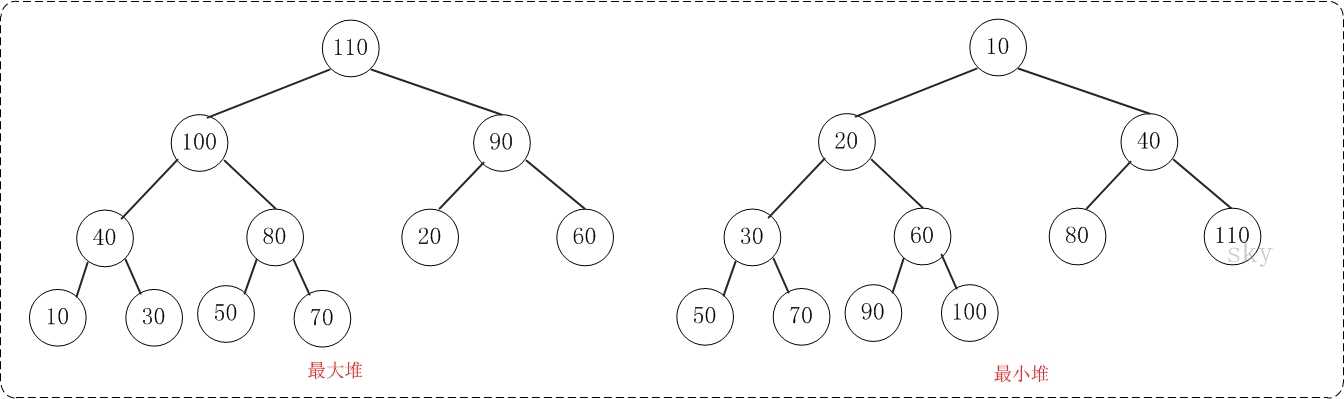
将任意节点不大于其子节点的堆叫做最小堆或小根堆
,而将任意节点不小于其子节点的堆叫做最大堆或大根堆
。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。
二叉堆的定义
二叉堆是完全二元树或者是近似完全二元树,它分为两种: 最大堆和最小堆
。
最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。示意图如下:
二叉堆一般都通过" 数组
"来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。有时候,我们将"二叉堆的第一个元素"放在数组索引0的位置,有时候放在1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。
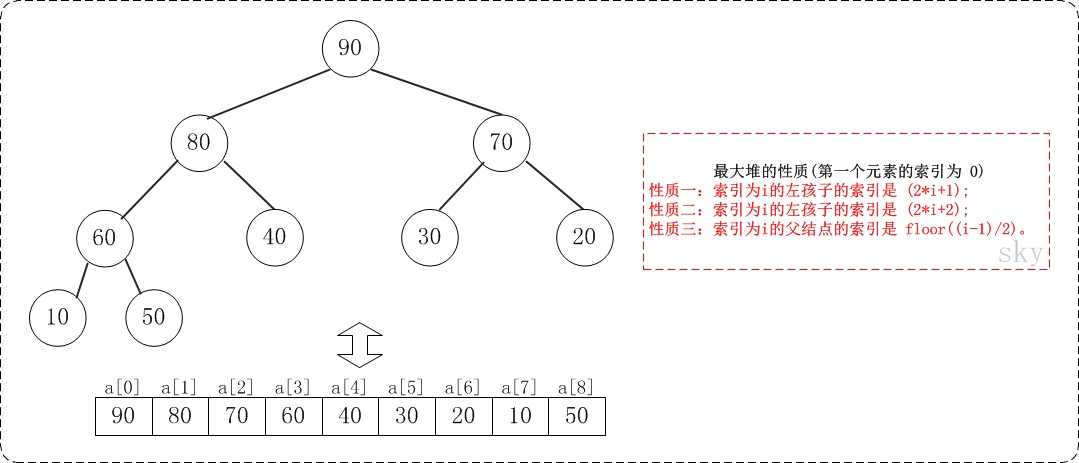
假设"第一个元素"在数组中的索引为0的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2*i+1);
(02) 索引为i的左孩子的索引是 (2*i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);
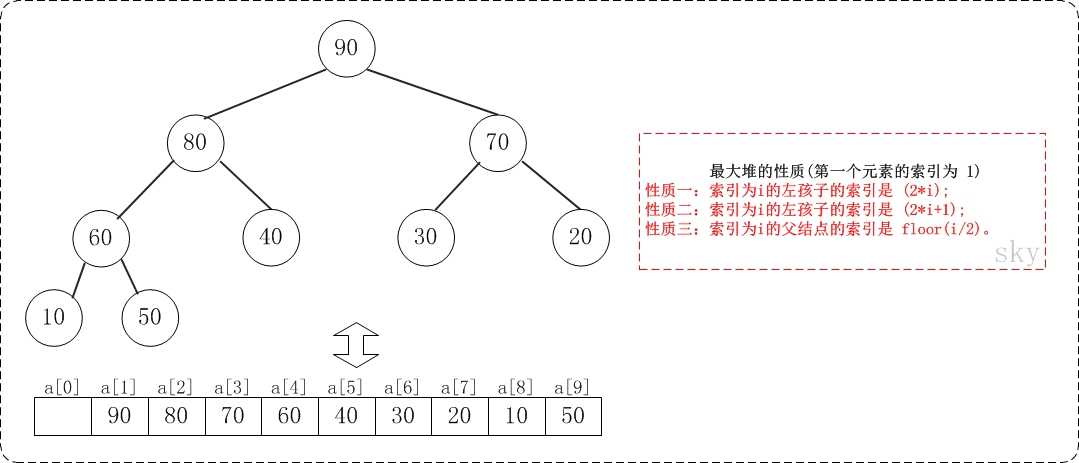
假设"第一个元素"在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2*i);
(02) 索引为i的左孩子的索引是 (2*i+1);
(03) 索引为i的父结点的索引是 floor(i/2);
注意:本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式!
在前面,我们已经了解到:"最大堆"和"最小堆"是对称关系。这也意味着,了解其中之一即可。本节的图文解析是以"最大堆"来进行介绍的。
二叉堆的核心是"添加节点"和"删除节点",理解这两个算法,二叉堆也就基本掌握了。下面对它们进行介绍。
1. 添加
假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85,需要执行的步骤如下:
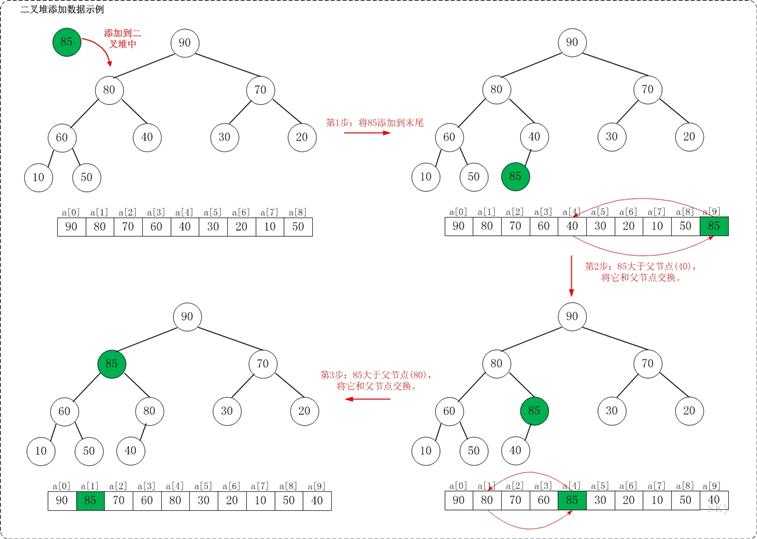
如上图所示,当向最大堆中添加数据时:先将数据加入到最大堆的最后,然后尽可能把这个元素往上挪,直到挪不动为止!
将85添加到[90,80,70,60,40,30,20,10,50]中后,最大堆变成了[90,85,70,60,80,30,20,10,50,40]。
最大堆的插入代码(C语言)
/*
* 最大堆的向上调整算法(从start开始向上直到0,调整堆)
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
static void maxheap_filterup(int start){
int c = start; // 当前节点(current)的位置
int p = (c-1)/2; // 父(parent)结点的位置
int tmp = m_heap[c]; // 当前节点(current)的大小
while(c > 0){
if(m_heap[p] >= tmp)
break;
else{
m_heap[c] = m_heap[p];
c = p;
p = (p-1)/2;
}
}
m_heap[c] = tmp;
}
/*
* 将data插入到二叉堆中
* 返回值: 0,表示成功;-1,表示失败
*/
int maxheap_insert(int data){
// 如果"堆"已满,则返回
if(m_size == m_capacity)
return -1;
m_heap[m_size] = data; // 将"数组"插在表尾
maxheap_filterup(m_size); // 向上调整堆
m_size++; // 堆的实际容量+1
return 0;
}
maxheap_insert(data)的作用:将数据data添加到最大堆中。
当堆已满的时候,添加失败;否则data添加到最大堆的末尾。然后通过上调算法重新调整数组,使之重新成为最大堆。
2. 删除
假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90,需要执行的步骤如下:
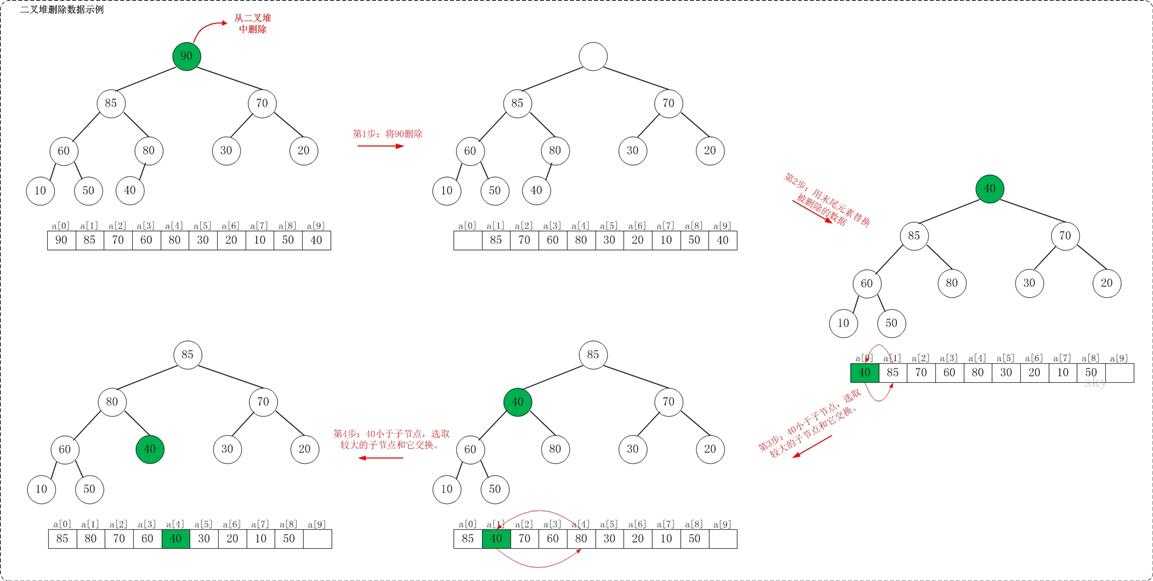
从[90,85,70,60,80,30,20,10,50,40]删除90之后,最大堆变成了[85,80,70,60,40,30,20,10,50]。
如上图所示,当从最大堆中删除数据时:先删除该数据,然后用最大堆中最后一个的元素插入这个空位;接着,把这个“空位”尽量往上挪,直到剩余的数据变成一个最大堆。
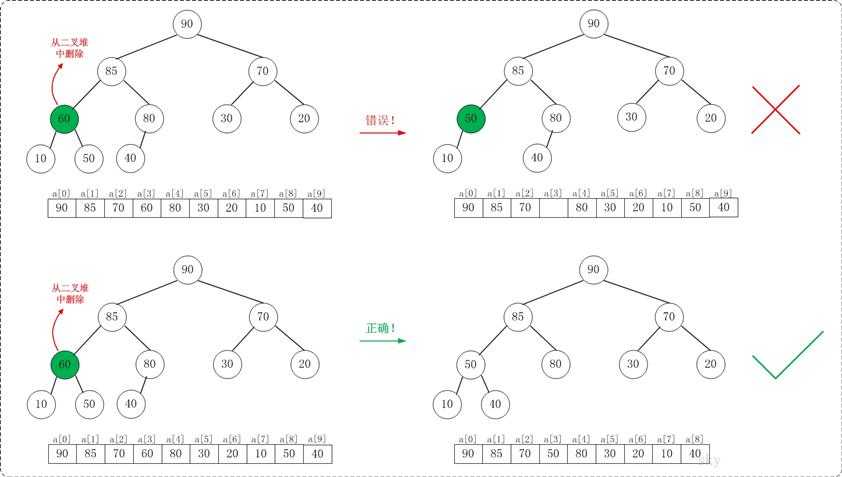
注意:考虑从最大堆[90,85,70,60,80,30,20,10,50,40]中删除60,执行的步骤不能单纯的用它的子节点来替换;而必须考虑到"替换后的树仍然要是最大堆"!
最大堆的删除代码(C语言)
/*
* 返回data在二叉堆中的索引
* 返回值: 存在 -- 返回data在数组中的索引不存在 -- -1
*/
int get_index(int data){
int i=0;
for(i=0; i<m_size; i++)
if (data==m_heap[i])
return i;
return -1;
}
/*
* 最大堆的向下调整算法
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 参数说明:
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
static void maxheap_filterdown(int start, int end){
int c = start; // 当前(current)节点的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = m_heap[c]; // 当前(current)节点的大小
while(l <= end){
// "l"是左孩子,"l+1"是右孩子
if(l < end && m_heap[l] < m_heap[l+1])
l++; // 左右两孩子中选择较大者,即m_heap[l+1]
if(tmp >= m_heap[l])
break; //调整结束
else{
m_heap[c] = m_heap[l];
c = l;
l = 2*l + 1;
}
}
m_heap[c] = tmp;
}
/*
* 删除最大堆中的data
* 返回值: 0,成功;-1,失败
*/
int maxheap_remove(int data){
int index;
// 如果"堆"已空,则返回-1
if(m_size == 0)
return -1;
// 获取data在数组中的索引
index = get_index(data);
if (index==-1)
return -1;
m_heap[index] = m_heap[--m_size]; // 用最后元素填补
maxheap_filterdown(index, m_size-1); // 从index位置开始自上向下调整为最大堆
return 0;
}
maxheap_remove(data)的作用:从最大堆中删除数据data。 当堆已经为空的时候,删除失败;否则查处data在最大堆数组中的位置。找到之后,先用最后的元素来替换被删除元素;然后通过下调算法重新调整数组,使之重新成为最大堆。该"示例的完整代码"以及"最小堆的相关代码",请参考下面的二叉堆的实现。
标签:
原文地址:http://www.cnblogs.com/wxgblogs/p/5727026.html