标签:
本节课将开始学习Deep NLP的基础——词向量模型。
word vector是一种在计算机中表达word meaning的方式。在Webster词典中,关于meaning有三种定义:
这三种定义由具象到抽象,但对于Deep NLP而言,处理的难度却是由难入易。
传统的NLP领域里主要是针对第一种定义——word representation——进行研究。例如,通过在一张描述语义关系的拓扑图(WordNet)上定义的上义词(Hypernyms)和同义词(Synonym),进而给出word在计算机中的表达。但这种方式存在很多问题。
首先,由于大多数词都有着属于自己独特的语境,例如,我们会说某人在某个领域是一个专家(expert),也会称赞某人的语言很流利(proficient)。虽然在WordNet中expert和proficient被定义为是一对同义词,但显然我们不能说某人在某个领域很proficient。这种一刀切的定义上义词和同义词的方式显然不够精细。
其次,语言的变化日新月异。而这种人工定义WordNet的方式显然跟不上变化的步伐。此外,人类对自然语言理解的主观性,以及在标注和维护WordNet时消耗的大量人力,都成为了制约WordNet发展的瓶颈。
最后,也是最糟糕的问题是,对于计算机而言,这种基于WordNet的词义定义方式很难对两个word之间的语义相似度进行准确的计算。我们只能粗劣地对两个词是否同义给出一个二分类的结果。
WordNet的这些问题是词的离散化表达(discrete representation)所带来的通病。除了WordNet,还有很多基于规则或是统计的NLP模型将word视为一个独立的原子单元(atomic symbols)进行处理。例如,在经典的VSM模型里,每一个word都被表示为一个one-hot向量(除了一个索引下标对应的位置是11,其他位置上的元素都是00)。显然,在这种表达方式下,对任意两个word计算出来的相似度都是00。此外,one-hot向量表达还存在着数据稀疏性和维度灾难的问题。
于是,人们想出了一种新的word meaning的定义方式:通过一个word相邻的词来定义这个word的meaning。这个定义来源于一个古老的idea(J.R.Firth, 1957):
You shall know a word by the company it keeps
并成为了包括传统NLP模型和今天将要介绍的word2vec模型在内的大部分word representation模型的基础。
具体来说,我们通过从大量的语料文本中构建一个co-occurrence矩阵来定义word representation。矩阵的构造通常有两种方式:基于document和基于windows。
通过统计word与document共现的次数得到的矩阵被称为word-document矩阵。这个矩阵一般被用于主题模型。相同主题的word之间往往有着较高的相似度。但该矩阵很难描述word的语法信息(例如POS tag)。
我们在课堂上主要讲授的是第二类矩阵:word-context矩阵。通过统计一个事先指定大小的窗口内的word共现次数,不仅可以刻画word的语义信息,还在一定程度上反应了word的语法结构信息。
举一个简单的例子。假设我们的语料库由三句话构成:
- I like deep learning.
- I like NLP.
- I enjoy flying.
设置统计窗口的大小为11,并采用对称窗口(与之相对的是非对称窗口,即仅考虑目标词左侧或右侧的上下文),则可以得到word-context矩阵如下: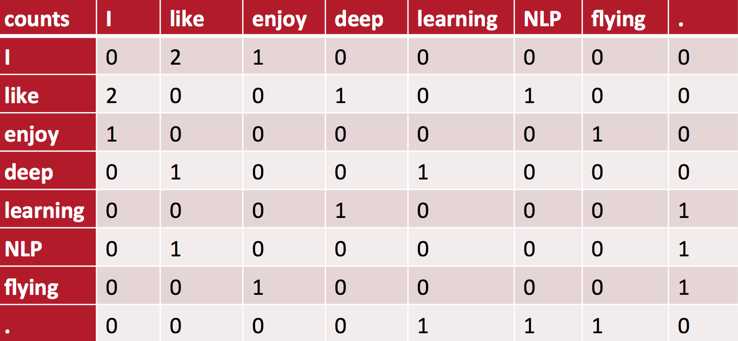
矩阵里的元素是列向量所代表的word出现在行向量所代表的word的上下文里的次数。(注意,我们并没有对句首或句尾的词做任何特殊的处理:比如增加一个S或E的标记Token作为句首或句尾的padding。)
现在,我们可以用矩阵的行向量来计算word之间的相似度了。
然而, 这种定义方式得到的词向量的维度等于词典的大小。这意味着,我们需要大量的空间来存储这些高维的词向量。同时,伴随着高维向量出现的数据稀疏性问题,也使得基于这些词向量的机器学习模型的训练变得异常困难。
简单来说,co-occurrence矩阵定义的词向量在一定程度上缓解了one-hot向量相似度为00的问题,但没有解决数据稀疏性和维度灾难的问题。
既然基于co-occurrence矩阵得到的离散词向量存在着高维和稀疏性的问题,一个自然而然的解决思路是对原始词向量进行降维,从而得到一个稠密的连续词向量。
第一个出场的对原始矩阵进行降维的方法是奇异值分解(SVD)。SVD的基本思想是,通过将原co-occurrence矩阵XX分解为一个正交矩阵UU,一个对角矩阵SS,和另一个正交矩阵VV乘积的形式,并提取UU的kk个主成分(按SS里对角元的大小排序)构造低维词向量。(关于SVD更多的介绍可以参考这篇博客:机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用)
除此之外,在对原始矩阵XX的处理上,还有很多简单但很好用的Hacks。比如对原始矩阵中高频词的降频处理;带权重的统计窗口(距离越近的词对词义的贡献越大);用Pearson相关性系数替代简单的词频统计等。包括我们后面要学习到的word2vec模型,也属于这一类Hacks。
即便是简单的对co-occurrence矩阵进行SVD分解得到的稠密词向量,也具有很多优美的性质。语义相近的词(比如"wrist"和"ankle")可以通过用词向量内积定义的相似度聚类到一起;同一动词的不同时态也往往出现在向量空间的同一片区域。词向量甚至可以一定程度上反应word之间的线性联系。
然而,高昂的计算复杂度(O(mn2)O(mn2))是SVD算法的性能瓶颈。这对于现在动辄上百万甚至上亿数据量的语料库而言,是一笔巨大的计算开销。更不用说每一个新词的加入都需要在一个新的矩阵上重新运行一遍SVD分解。此外,后面我们会看到,SVD算法和其他Deep Learning模型本质上是属于两类不同的学习算法。
尽管SVD分解存在着这样或那样的问题,但是其将word表示为一个稠密的低维连续向量的思想,成为了包括Deep NLP在内的众多NLP模型的基础。
From now on, every word will be a dense vector.
接下来,我们来看下Deep Learning是如何从原始的语料库中直接学习到低维词向量的表达。这也是我们学习的第一个Deep NLP模型——word2vec模型。
与直接从co-occurrence矩阵里提取词向量的SVD算法不同,word2vec模型背后的基本思想是对出现在上下文环境里的词进行预测(事实上,后面会看到,这种对上下文环境的预测本质上也是一种对co-occurrence统计特征的学习)。对于每一条输入文本,我们选取一个上下文窗口和一个中心词,并基于这个中心词去预测窗口里其他词出现的概率。因此,word2vec模型可以方便地从新增语料中学习到新增词的向量表达,是一种高效的在线学习算法(online learning)。
对于一个长度为TT的语料库,假设我们为每一个词选取的上下文窗口的大小是mm(指的是上下文各mm个词),则我们的目标函数是最大化训练语料的对数似然概率:
一个简单的计算条件概率p(wt+j|wt)p(wt+j|wt)的公式如下:
对机器学习有一定基础的同学会发现,这里的条件概率其实是一个Softmax分类函数,而目标函数对应着这个分类函数的交叉熵。
优化这个目标函数的算法是SGD——随机梯度下降法。为此,我们要求解这个目标函数的一阶导数。
首先,我们引入两个重要的求导法则:
有线性代数和微积分基础的同学可以轻松证明这两个法则的正确性。
接下来,我们首先对"center"向量vcvc进行求导: