标签:
[BZOJ3160]万径人踪灭
试题描述
.jpg)
.jpg)
输入
.jpg)
输出
输入示例
见“输入”
输出示例
见“输入”
数据规模及规定
题解
问题分为两部分:
一. 对于每一个分界点(某个位置)或分界线(某两个位置中间),要求这么一个东西
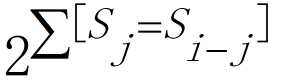
意思就是回文串要求左半部分与右半部分对称,那么找到这些对称的位置,每个位置有选择或者不选两种情况,所以是 2 的那么多次方。
求法:因为原串只有 a, b 两种字符,所以把 a 设成 1,b 设成 0 求一次卷积,再把 b 设成 1,a 设成 0 求一次卷积,加起来即可。
二. 排除连续的情况
不会用回文自动机的我只好 hash + 二分。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 260010
#define MOD 1000000007
#define ULL unsigned long long
const double pi = acos(-1.0);
int n;
ULL hashl[maxn], hashr[maxn], hashl2[maxn], hashr2[maxn], id2[maxn], id3[maxn];
char S[maxn];
struct Complex {
double a, b;
Complex() { a = b = 0.0; }
Complex operator + (const Complex& t) const {
Complex ans;
ans.a = a + t.a;
ans.b = b + t.b;
return ans;
}
Complex operator - (const Complex& t) const {
Complex ans;
ans.a = a - t.a;
ans.b = b - t.b;
return ans;
}
Complex operator * (const Complex& t) const {
Complex ans;
ans.a = a * t.a - b * t.b;
ans.b = a * t.b + b * t.a;
return ans;
}
Complex operator *= (const Complex& t) {
*this = *this * t;
return *this;
}
} a[maxn<<1], b[maxn<<1];
int tar[maxn];
void FFT(Complex* a, int n, int tp) {
for(int i = 0; i < n; i++) if(i < tar[i]) swap(a[i], a[tar[i]]);
for(int i = 1; i < n; i <<= 1) {
Complex w, wn; wn.a = cos(pi / i); wn.b = sin(pi / i) * tp;
for(int j = 0; j < n; j += (i << 1)) {
w.a = 1.0; w.b = 0.0;
for(int k = 0; k < i; k++) {
Complex t1 = a[j+k], t2 = a[j+k+i] * w;
a[j+k] = t1 + t2;
a[j+k+i] = t1 - t2;
w *= wn;
}
}
}
if(tp < 0) for(int i = 0; i <= n; i++) a[i].a = a[i].a / (double)n + .5;
return ;
}
ULL lstr(int l, int r) { l++, r++; return hashl[r] - hashl[l-1] * id2[r-l+1]; }
ULL rstr(int l, int r) { l++, r++; return hashr[l] - hashr[r+1] * id2[r-l+1]; }
ULL lstr2(int l, int r) { l++, r++; return hashl2[r] - hashl2[l-1] * id3[r-l+1]; }
ULL rstr2(int l, int r) { l++, r++; return hashr2[l] - hashr2[r+1] * id3[r-l+1]; }
int two[maxn], ans, Len;
bool check(int i, int mid) {
int ll = (i >> 1) - mid + 1, lr = (i >> 1), rl = (i & 1) ? (i >> 1) + 1 : lr, rr = rl + mid - 1;
bool res = ll >= 0 && rr < Len && (rstr(ll, lr) == lstr(rl, rr)) && (rstr2(ll, lr) == lstr2(rl, rr));
// if((i >> 1) == 127) printf("%d(%c) %d(%c) %d(%c) %d(%c) %llu %llu\t", ll, S[ll], lr, S[lr], rl, S[rl], rr, S[rr], rstr(ll, lr), lstr(rl, rr));
return ll >= 0 && rr < Len && rstr(ll, lr) == lstr(rl, rr) && rstr2(ll, lr) == lstr2(rl, rr);
}
int main() {
scanf("%s", S);
int m = strlen(S) - 1; Len = strlen(S);
int L = 0;
for(n = 1; n <= (m << 1); n <<= 1) L++;
for(int i = 0; i < n; i++) tar[i] = (tar[i>>1] >> 1) | ((i & 1) << L - 1);
for(int i = 0; i <= m; i++) a[i].a = (double)(S[i] == ‘a‘);
FFT(a, n, 1);
for(int i = 0; i <= n; i++) a[i] *= a[i];
for(int i = 0; i <= m; i++) b[i].a = (double)(S[i] == ‘b‘);
FFT(b, n, 1);
for(int i = 0; i <= n; i++) b[i] *= b[i], a[i] = a[i] + b[i];
FFT(a, n, -1);
for(int i = 0; i <= (m << 1); i++) a[i].a = (double)((int)a[i].a + 1 >> 1), b[i].a = (double)((int)b[i].a + 1 >> 1);
// for(int i = 0; i <= (m << 1); i++) printf("%d ", (int)a[i].a); putchar(‘\n‘);
two[0] = 1;
for(int i = 1; i <= m; i++) {
two[i] = two[i-1] << 1;
if(two[i] > MOD) two[i] -= MOD;
}
hashl[0] = 0;
for(int i = 1; i <= m + 1; i++) hashl[i] = hashl[i-1] * 2 + S[i-1] - ‘a‘;
hashr[m+2] = 0;
for(int i = m + 1; i; i--) hashr[i] = hashr[i+1] * 2 + S[i-1] - ‘a‘;
id2[0] = 1;
for(int i = 1; i <= m + 1; i++) id2[i] = id2[i-1] * 2;
hashl2[0] = 0;
for(int i = 1; i <= m + 1; i++) hashl2[i] = hashl2[i-1] * 3 + S[i-1] - ‘a‘;
hashr2[m+2] = 0;
for(int i = m + 1; i; i--) hashr2[i] = hashr2[i+1] * 3 + S[i-1] - ‘a‘;
id3[0] = 1;
for(int i = 1; i <= m + 1; i++) id3[i] = id3[i-1] * 3;
m++, m <<= 1; int tmp = 0;
for(int i = 0; i <= m - 2; i++) {
ans += two[(int)a[i].a];
int l = 0, r = min((i >> 1) + 1, (i & 1) ? (m >> 1) - (i >> 1) : (m >> 1) - (i >> 1) + 1) + 1;
while(l < r - 1) {
int mid = l + r >> 1;
if(check(i, mid)) l = mid; else r = mid;
}
if(check(i, l + 1)) l++;
ans -= l + 1;
if(ans < 0) ans += MOD;
if(ans > MOD) ans -= MOD;
}
printf("%d\n", ans);
return 0;
}
/*
abaabaa
*/
标签:
原文地址:http://www.cnblogs.com/xiao-ju-ruo-xjr/p/5728349.html