标签:


题意
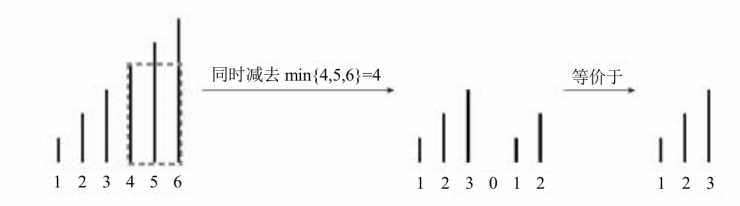
给出一个1~n的序列,每一次都可以选择一些数减去1,问最小次数使得所有数都为0是多少?
题解
1.可以先模拟最优策略,那么很显然,每次选择一半的数就是最优的。
代码
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n,cnt;
int main(){
freopen("seq.in","r",stdin);
freopen("seq.out","w",stdout);
scanf("%d",&n);
while(n){
n>>=1;
cnt++;
}
cout<<cnt<<endl;
return 0;
}


题意
求出一个点到其他所有点的最大权值,而这个一个点u到另外一个点v的权值是u到v整个路径的最小边权。
题解
1.最暴力的做法就是枚举每一点算出到每一个点的的权值,再加起来求max。
2.由于数据范围一般是nlogn或者n,那么就不枚举点了,枚举边但是边要受权值小的的限制,那就直接从大到小排序不就好了就没有后效性了。
3.对于一条边连着左右两部分,当考虑到这一条边的时候,这一条边的权值一定是相对于考虑过的边是最小的w,就先用并查集把边相连的两部分连在一起。
4.假设我们想要的那个点在左边,那么左边的权值ResLeft就应该加上右边的点数RightSize*w,整体的权值为ResLeft = ResLeft+RightSize*w,假设我们想要的那个点在右边,那么右边边的权值ResRight就应该加上右边的点数LeftSize*w,整体的权值就为ResRight = ResRight+LeftSize*w,然后这个整体的权值就是max(ResLeft,ResRight)
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 500010;
int fa[N],size[N],n,u,v,w,res[N];
struct Edge{
int u,v,w;
bool operator < (const Edge&rhs)const{return w > rhs.w;}
}edge[N<<1];
int find(int x){
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int main(){
freopen("ljqz.in","r",stdin);
freopen("ljqz.out","w",stdout);
scanf("%d",&n);
for(int i = 1;i < n;++i){
scanf("%d%d%d",&u,&v,&w);
edge[i] = (Edge){u,v,w};
}
sort(edge+1,edge+n);
for(int i = 1;i <= n;++i)fa[i] = i,size[i] = 1;
for(int i = 1;i < n;++i){
int fx = find(edge[i].u),fy = find(edge[i].v);
if(fx != fy)fa[fx] = fy;
res[fx] += size[fy]*edge[i].w;
res[fy] += size[fx]*edge[i].w;
size[fy] += size[fx];
res[fy] = max(res[fy],res[fx]);
}
cout<<res[find(n)]<<endl;
return 0;
}




题意
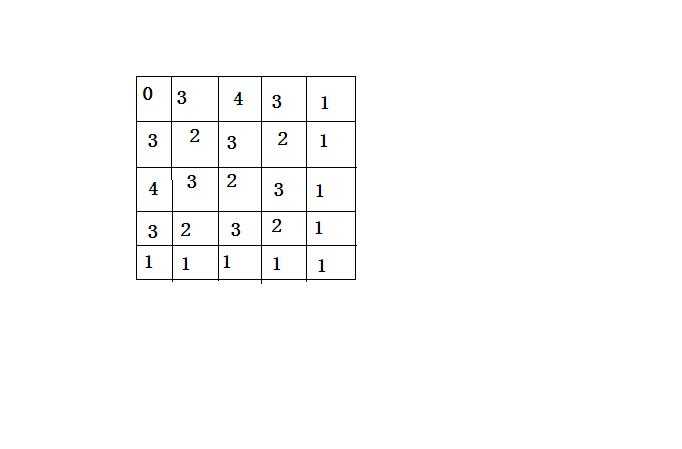
给出方针左上角的点,要求横向纵向斜向都为素数,并且位数和为sum,按字典序输出质数方阵
题解
一.最暴力的方法就是枚举矩阵里面的每一个数为O(1025).
二.其次暴力可以打表的就是把以某一个数开头的素数记录下来,枚举第一行,再枚举第一二三四五列,最后再判断是否满足条件。
三.0.正解就是优美的暴力,涨姿势了。
1.因为很显然的就是每一个素数都是以1,3,7,9结尾的,那么最后一行和最后一列的素数组成都为1,3,7,9限制级别为最高。
2.其次就是斜行相交的格子的数要相同,并且会受到最后一行和最后一列和左上角那个点的影响,限制级别其次。
3.然后就可以通过填过的数字直接暴力枚举了,限制级别最低。
4.最后就可以通过枚举的数字算出一些格子,来判断是否符合条件。
就按照限制级别开始枚举,流程图:
代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100000;
#define clr(a,b) memset(a,b,sizeof(a))
int primelist[N],las[N];
int map[5][5],sum,hash[10][10][10][10][10],tot,b[10][110][10],a[10][10][100],vis[N],num[5];
struct res{
int x[5];
bool operator < (const res &rhs)const{
if(x[0] == rhs.x[0] && x[1] == rhs.x[1] && x[2] == rhs.x[2] && x[3] == rhs.x[3])return x[4]<rhs.x[4];
if(x[0] == rhs.x[0] && x[1] == rhs.x[1] && x[2] == rhs.x[2])return x[3] < rhs.x[3];
if(x[0] == rhs.x[0] && x[1] == rhs.x[1])return x[2] < rhs.x[2];
if(x[0] == rhs.x[0])return x[1] < rhs.x[1];
return x[0] < rhs.x[0];
}
}ans[300];
void DfsElse(int va,int vb,int vc,int vd){
map[0][1] = va/10000,map[2][1] = (va/100)%10;
map[0][3] = vb/10000,map[2][3] = (vb/100)%10;
map[1][0] = vc/10000,map[1][2] = (vc/100)%10;
map[3][0] = vd/10000,map[3][2] = (vd/100)%10;
map[0][2] = sum-map[0][0]-map[0][1]-map[0][3]-map[0][4];
map[2][0] = sum-map[2][1]-map[2][2]-map[2][3]-map[2][4];
if(map[0][2]<= 0||map[0][2]>9||map[2][0]<= 0||map[2][0]>9)return;
if(map[0][2]+map[1][2]+map[2][2]+map[3][2]+map[4][2] != sum)return;
if(map[0][0]+map[0][1]+map[0][2]+map[0][3]+map[0][4] != sum)return;
if(!hash[map[0][0]][map[0][1]][map[0][2]][map[0][3]][map[0][4]])return;
if(!hash[map[0][2]][map[1][2]][map[2][2]][map[3][2]][map[4][2]])return;
if(!hash[map[2][0]][map[2][1]][map[2][2]][map[2][3]][map[2][4]])return;
if(!hash[map[0][0]][map[1][0]][map[2][0]][map[3][0]][map[4][0]])return;
++tot;
for(int i = 0;i < 5;++i){
for(int j = 0;j < 5;++j){
ans[tot].x[i] = ans[tot].x[i]*10+map[i][j];
}
}
}
void DfsMid(int va,int vb){
for(int i = 4;i >= 0;--i)map[i][i] = va % 10,va /= 10;
for(int i = 4;i >= 0;--i)map[4-i][i] = vb % 10,vb /= 10;
int cnt1 = b[map[1][1]][map[3][1]*10+map[4][1]][0];
int cnt2 = b[map[1][3]][map[3][3]*10+map[4][3]][0];
int cnt3 = b[map[1][1]][map[1][3]*10+map[1][4]][0];
int cnt4 = b[map[3][1]][map[3][3]*10+map[3][4]][0];
// printf("%d %d %d %d\n",cnt1,cnt2,cnt3,cnt4);
for(int i = 1;i <= cnt1;++i)
for(int j = 1;j <= cnt2;++j)
for(int k = 1;k <= cnt3;++k)
for(int l = 1;l <= cnt4;++l)
DfsElse(b[map[1][1]][map[3][1]*10+map[4][1]][i],b[map[1][3]][map[3][3]*10+map[4][3]][j],b[map[1][1]][map[1][3]*10+map[1][4]][k],b[map[3][1]][map[3][3]*10+map[3][4]][l]);
}
void DfsUnderAndRight(int va,int vb){
for(int i = 4;i >= 0;--i)map[4][i] = va % 10,va /= 10;
for(int i = 4;i >= 0;--i)map[i][4] = vb % 10,vb /= 10;
int cnt1 = a[map[0][0]][map[4][4]][0];
int cnt2 = a[map[4][0]][map[0][4]][0];
// printf("%d %d\n",cnt1,cnt2);
for(int i = 1;i <= cnt1;++i){
for(int j = 1;j <= cnt2;++j){
int x = a[map[0][0]][map[4][4]][i];
int y = a[map[4][0]][map[0][4]][j];
if((x/100)%10 == (y/100)%10)DfsMid(x,y);
}
}
}
int main(){
freopen("prime.in","r",stdin);
freopen("prime.out","w",stdout);
scanf("%d%d",&sum,&map[0][0]);
for(int i = 2;i <= N;++i)if(!vis[i]){
primelist[++primelist[0]] = i;
for(int j = 2*i;j <= N;j += i)vis[j] = 1;
}
for(int i = 1;i <= primelist[0];++i)if(primelist[i]>=10000){
int x = primelist[i],numcnt = 5,add = 0,flag = 1;clr(num,0);
while(x){
add += x%10;
if(x%2 == 0 || x%10 == 5)flag = 0;
x /= 10;
}
if(add != sum)continue;
x = primelist[i];
if(flag)las[++las[0]] = x;
a[x/10000][x%10][++a[x/10000][x%10][0]] = x;
b[(x/1000)%10][x%100][++b[(x/1000)%10][x%100][0]] = x;
hash[x/10000][(x/1000)%10][(x/100)%10][(x/10)%10][x%10] = 1;
}
// for(int i = 1;i <= las[0];++i)printf("%d ",las[i]);
for(int i = 1;i <= las[0];++i){
for(int j = 1;j <= las[0];++j){
if(las[i]%10 == las[j]%10)DfsUnderAndRight(las[i],las[j]);
}
}
sort(ans+1,ans+tot+1);
for(int i = 1;i <= tot;++i){
for(int j = 0;j < 5;++j)printf("%d\n",ans[i].x[j]);
puts("");
}
return 0;
}
标签:
原文地址:http://www.cnblogs.com/xgtao984/p/5731416.html