标签:
题目链接:http://poj.org/problem?id=2253
题意:
给出两只青蛙的坐标A、B,和其他的n-2个坐标,任一两个坐标点间都是双向连通的。显然从A到B存在至少一条的通路,每一条通路的元素都是这条通路中前后两个点的距离,这些距离中又有一个最大距离。
现在要求求出所有通路的最大距离,并把这些最大距离作比较,把最小的一个最大距离作为青蛙的最小跳远距离。
思路:
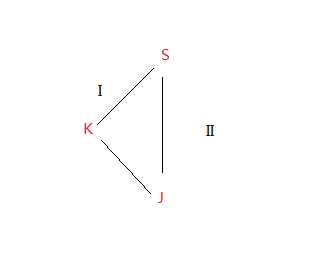
j从1,2,两条路中选取较小者,而1这条路,是s—>k—>j的最大步伐。
#include <stdio.h> #include <string.h> #include <math.h> #include <algorithm> using namespace std; #define INF 0x3f3f3f3f struct Point { double x; double y; } points[300]; double maps[305][305]; bool vis[305]; double dis[305]; int n; void Dijkstra(int s) { memset(vis,false,sizeof(vis)); for(int i=1;i<=n;i++) dis[i] = maps[s][i]; vis[s] = true; for(int i=1;i<n;i++) { int k = 0,tmp = INF; for(int j=1;j<=n;j++) { if(vis[j]) continue; if(dis[j]<tmp) { tmp = dis[j]; k = j; } } vis[k] = true; for(int j=1;j<=n;j++) { if(vis[j]) continue; dis[j] = min(dis[j],max(dis[k],maps[k][j])); } } } int main() { int cases = 1; while(scanf("%d",&n),n) { for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) maps[i][j] = INF; for(int i=1; i<=n; i++) scanf("%lf%lf",&points[i].x,&points[i].y); for(int i=1; i<=n; i++) { for(int j=i+1; j<=n; j++) { double tx = points[i].x - points[j].x; double ty = points[i].y - points[j].y; maps[i][j] = maps[j][i] = sqrt(tx*tx+ty*ty); } } Dijkstra(1); printf("Scenario #%d\nFrog Distance = %.3lf\n\n",cases++,dis[2]); } return 0; }
标签:
原文地址:http://www.cnblogs.com/TreeDream/p/5731660.html