标签:
%传递矩阵法求简支梁固有频率的近似解
clc
clear
syms p q
Sp = sym(‘[1 0 0 0;0 1 0 0;0 0 1 0;x 0 0 1]‘); %点传递矩阵
Sf = sym(‘[1 1 1/2 1/6;0 1 1 1/2;0 0 1 1;0 0 0 1]‘); %场传递矩阵
n = input(‘输入划分单元数:‘);
S = ((Sf*Sp)^(n-1))*Sf; %两端支座之间的传递矩阵
%求固有频率
xs = solve(S(1,2)*S(3,4)-S(1,4)*S(3,2));
xs = sort(double(xs));
xt = xs*n^4;
xt = sqrt(xt);
xe(1:n-1) = (pi*(1:n-1)).^2; %精确解
xe = xe‘;
fprintf(‘传递矩阵法的结果:\n‘)
for i = 1:n-1
fprintf(‘第%d阶固有频率:%8.4f(EI/ml^3)^(1/2)\n‘,i,xt(i))
end
%求模态
step = 1/n;
for i = 1:n-1
f0 = -S(3,2)/S(3,4);
f0 = subs(f0,‘x‘,xs(i));
xk(:,1) = [0 1 0 f0]‘;
for j = 2:n+1
xk(:,j) = Sf*Sp*xk(:,j-1);
xk(:,j) = subs(xk(:,j),‘x‘,xs(i));
end
xkk = xk(1,2:n);
xkk = xkk/max(abs(xkk));
xkk = double(xkk);
xkk = real(xkk);
if(xkk(1)<0)
xkk = -xkk;
end
fprintf(‘第%d阶模态为:‘,i)
disp(xkk)
figure()
plot(0:step:1,[0 xkk 0].*abs(sin(i*pi*(0:step:1))),‘ro‘)
hold on
xx = 0:pi/200:1;
plot(xx,sin(i*pi*xx),‘b‘)
end
fprintf(‘精确解的结果:\n‘)
for i = 1:n-1
fprintf(‘第%d阶固有频率:%8.4f(EI/ml^3)^(1/2)\n‘,i,xe(i))
end
运行结果:
输入划分单元数:5
传递矩阵法的结果:
第1阶固有频率: 9.8684(EI/ml^3)^(1/2)
第2阶固有频率: 39.3808(EI/ml^3)^(1/2)
第3阶固有频率: 87.1779(EI/ml^3)^(1/2)
第4阶固有频率:143.5557(EI/ml^3)^(1/2)
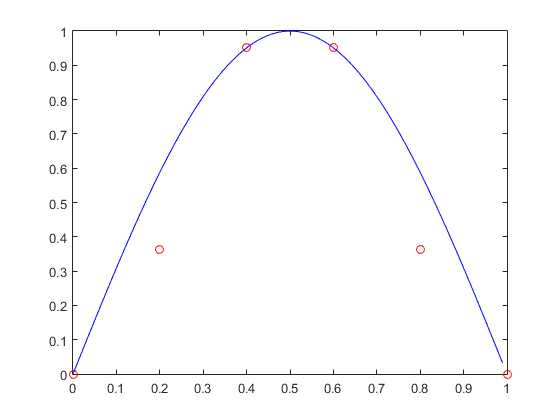
第1阶模态为: 0.6180 1.0000 1.0000 0.6180
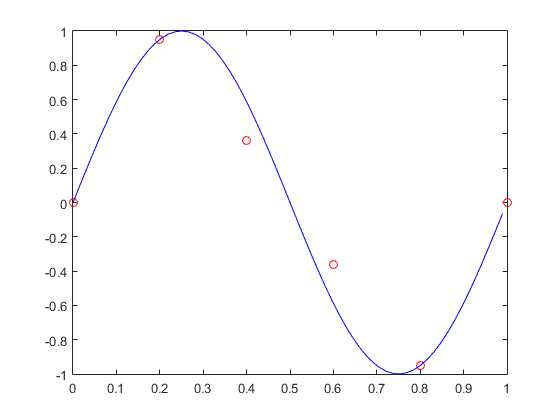
第2阶模态为: 1.0000 0.6180 -0.6180 -1.0000
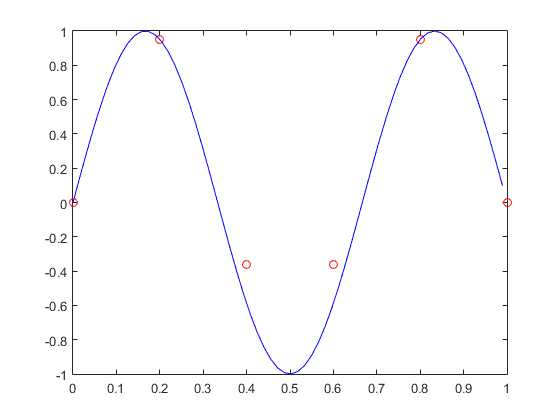
第3阶模态为: 1.0000 -0.6180 -0.6180 1.0000
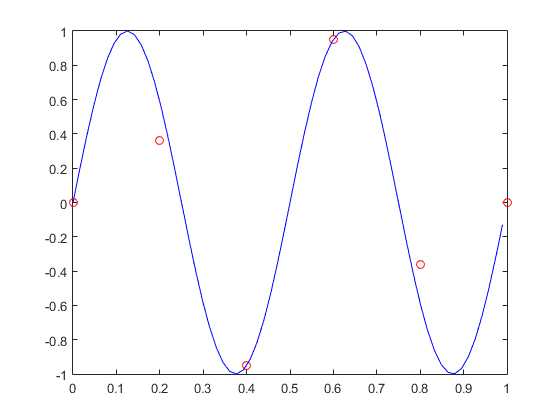
第4阶模态为: 0.6180 -1.0000 1.0000 -0.6180
精确解的结果:
第1阶固有频率: 9.8696(EI/ml^3)^(1/2)
第2阶固有频率: 39.4784(EI/ml^3)^(1/2)
第3阶固有频率: 88.8264(EI/ml^3)^(1/2)
第4阶固有频率:157.9137(EI/ml^3)^(1/2)
标签:
原文地址:http://www.cnblogs.com/zhanchao/p/5734063.html