标签：

分类和逻辑回归

接下来讨论分类问题，类似于回归问题，只不过y的值只有少数离散的值。现在我们考虑二分类问题，此时y只有0和1两个值。

逻辑回归

构造假设函数$h_{\theta}(x)$:

$h_{\theta}(x)=g(\theta^{(x)})=\frac{1}{1+e^{-\theta^{T}x}}$

其中

$g(z)=\frac{1}{1+e^{-z}}$

$g^{‘}(z)=g(z)(1-g(z))$

$g(z)$函数图像如下：

$g^{‘}(z)$函数图像如下：

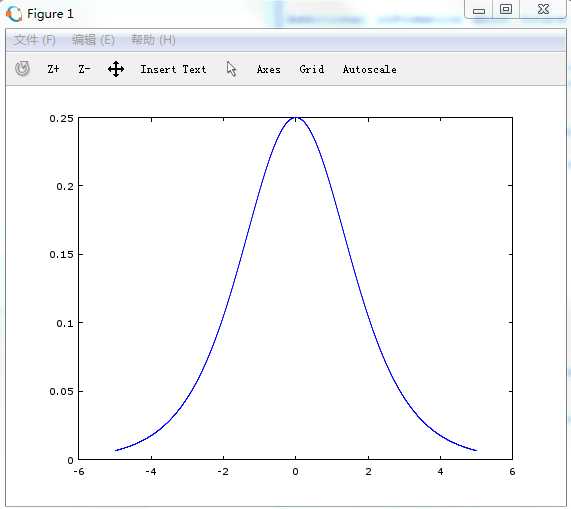
假设：

$P(y=1\mid x;\theta) = h_{\theta}(x)$

$P(y=0\mid x;\theta) = 1- h_{\theta}(x)$

等价于：

$P(y \mid x;\theta) = (h_{\theta}(x))^{y}(1- h_{\theta}(x))^{1-y}$

y取0或1

假设有m个训练样本，可以写出参数的概率公式：

$L(\theta) = p(\vec{y} \mid X; \theta)$

$L(\theta) =  \prod_{i=1}^{m}p(y^{(i)}\mid x^{(i)};\theta)$

$L(\theta) =  \prod_{i=1}^{m}  (h_{\theta}(x^{(i)}))^{y^{(i)}}(1- h_{\theta}(x^{(i)}))^{1-y^{(i)}} $

为了便于求解，先取对数：

$\iota(\theta) = logL(\theta)$

$\iota(\theta) = \sum_{i=1}^{m}y^{(i)}logh(x^{(i)}) + (1-y^{i()})log(1-h(x^{(i)}))$

单一训练样本下，求解梯度：

$\frac{\partial }{\partial  \theta_{j}}\iota(\theta) = (-h_{\theta}^{x})x_{j}$

因此，随机梯度下降法有：

$\theta_{j} := \theta_{j} + \alpha (y^{(i)} - h_{\theta}(x^{(i)}))x_{j}^{(i)}$

上式跟LMS更新规则很像，当学了GLM模型后便知原因。

第二章 分类和逻辑回归

标签：

原文地址：http://www.cnblogs.com/wuchaodzxx/p/5734524.html