标签:
呵呵哒。WA了无数次,一开始想的办法最终发现都有缺陷。首先需要知道:
1)线段不相交,一定面积为0
2)有一条线段与X轴平行,面积一定为0
3)线段相交,但是能接水的三角形上面线段把下面的线段完全覆盖。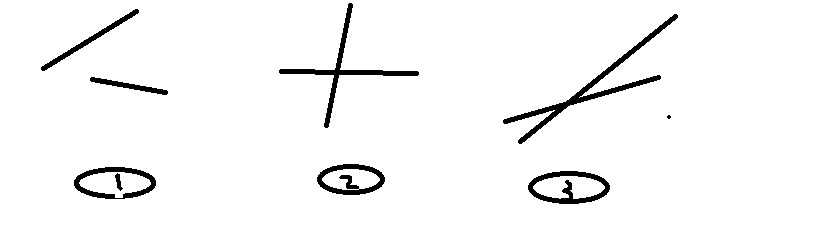
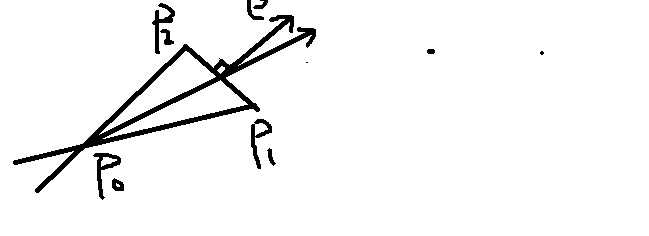
(1),(2)的情况简单,主要是解决(3)。下面对(3)进行讨论,如下图所示,设p1,p2是两线段各自位置较高的点,p0为两线段的交点,向量e是三角形p0p1p2的关于边p1p2的外侧法向量。则当e的终点位于第1,2象限时才会有积水,3,4象限是没有的。判断e的方向可以根据它与(p0p1+p0p2)的点积,e与(p0p1+p0p2)的点积总是大于0的。
#define _CRT_SECURE_NO_DEPRECATE #include<iostream> #include<cmath> #include<algorithm> using namespace std; const double PI = acos(-1.0); const int N = 300; const double EPS = 1e-8;//实数精度 //点结构类型 struct Point{ double x, y; Point(double a = 0, double b = 0){ x = a; y = b; } }; //线段结构类型 struct LineSeg{ Point s, e; LineSeg(){}; LineSeg(Point a, Point b) : s(a), e(b){} }; struct Line{ double a, b, c; }; Point operator-(Point a, Point b){ return Point(a.x - b.x, a.y - b.y); } //重载==,判断点a,b是否相等 bool operator==(Point a, Point b){ return abs(a.x - b.x) < EPS&&abs(a.y - b.y) < EPS; } //比较实数r1与r2的大小关系 int RlCmp(double r1, double r2 = 0){ if (abs(r1 - r2) < EPS) return 0; return r1>r2 ? 1 : -1; } //返回向量p1-p0和p2-p0的叉积 double Cross(Point p0, Point p1, Point p2){ Point a = p1 - p0; Point b = p2 - p0; return a.x*b.y - b.x*a.y; } //判断线段L1与线段L2是否相交(包括交点在线段上) bool Intersect(LineSeg L1, LineSeg L2){ //排斥实验和跨立实验 return max(L1.s.x, L1.e.x) >= min(L2.s.x, L2.e.x) && min(L1.s.x, L1.e.x) <= max(L2.s.x, L2.e.x) && max(L1.s.y, L1.e.y) >= min(L2.s.y, L2.e.y) && min(L1.s.y, L1.e.y) <= max(L2.s.y, L2.e.y) && Cross(L1.s, L1.e, L2.s)*Cross(L1.s, L1.e, L2.e) <= 0 && Cross(L2.s, L2.e, L1.s)*Cross(L2.s, L2.e, L1.e) <= 0; } Line MakeLine(Point a, Point b){ Line L; L.a = (b.y - a.y); L.b = (a.x - b.x); L.c = (b.x*a.y - a.x*b.y); if (L.a < 0){ //保准x系数大于等于0 L.a = -L.a; L.b = -L.b; L.c = -L.c; } return L; } //判直线X,Y是否相交,相交返回true和交点 bool LineIntersect(Line X, Line Y, Point&P){ double d = X.a*Y.b - Y.a*X.b; if (d == 0) //直线平行或者重合 return false; P.x = (X.b*Y.c - Y.b*X.c) / d; P.y = (X.c*Y.a - Y.c*X.a) / d; return true; } Point HighPoint(Point a, Point b){ return a.y > b.y ? a : b; } Point LowPoint(Point a, Point b){ return a.y < b.y ? a : b; } double Dot(Point a, Point b){ return a.x*b.x + a.y*b.y; } double Area(LineSeg L1, LineSeg L2){ if (!Intersect(L1, L2)) return 0; //不相交 Line X = MakeLine(L1.s, L1.e); Line Y = MakeLine(L2.s, L2.e); if (RlCmp(X.a*Y.a) == 0) //有一条直线与x平行 return 0; Point inter; LineIntersect(X, Y, inter); //计算交点 double y = min(max(L1.e.y, L1.s.y), max(L2.e.y, L2.s.y)); double x1 = -(X.b*y + X.c) /X.a; double x2 = -(Y.b*y + Y.c) / Y.a; Point p1(x1, y), p2(x2, y); double area = abs(Cross(inter, p1, p2) / 2); //计算面积 if (RlCmp(X.b*Y.b) == 0) //有一条线与Y轴平行 return area; double k1 = -X.a / X.b; //X的斜率 double k2 = -Y.a / Y.b; //Y的斜率 Point high = HighPoint(HighPoint(L1.s, L1.e),HighPoint(L2.s, L2.e)); Point low = LowPoint(HighPoint(L1.s, L1.e), HighPoint(L2.s, L2.e)); if (RlCmp(high.y - low.y) == 0) return area; if (RlCmp(high.x - low.x) == 0) return 0; double k = -(high.x - low.x) / (high.y - low.y); Point mid((high.x + low.x) / 2, (high.y + low.y) / 2); Point op = mid - inter; Point ans; if (RlCmp(Dot(op, Point(1, k))) >= 0) ans = Point(1, k); else ans = Point(-1, -k); if ((ans.x > 0 && ans.y > 0 || (ans.x<0 && ans.y>0))) return area; else return 0; } int main(){ int T; double a, b, c, d; scanf("%d", &T); while (T--){ scanf("%lf%lf%lf%lf", &a, &b, &c, &d); LineSeg L1(Point(a, b), Point(c, d)); scanf("%lf%lf%lf%lf", &a, &b, &c, &d); LineSeg L2(Point(a, b), Point(c, d)); double area = Area(L1, L2); printf("%.2lf\n", area); } return 0; }
标签:
原文地址:http://www.cnblogs.com/td15980891505/p/5735295.html