标签：
根据台大的机器学习在Coursera上公开课《机器学习基石》和《机器学习技术》整理的笔记，考虑到现在该课程已经关闭了，所以我把我的学习笔记慢慢整理出来。这是第一篇-Linear SVM
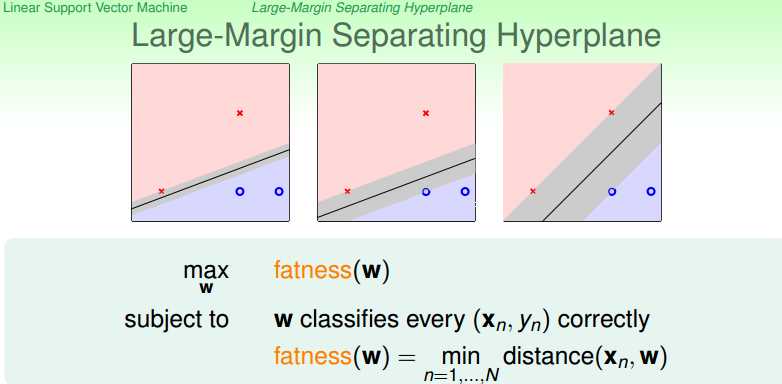
如果我们采用PLA(Percetron Learning Algorithmn)，已经能够得到若干种w,这些w都能够正确地把两类点区分开来，那么我们如何在这些w中挑出我们喜欢的那个w呢，这就是线性SVM需要解决的问题。
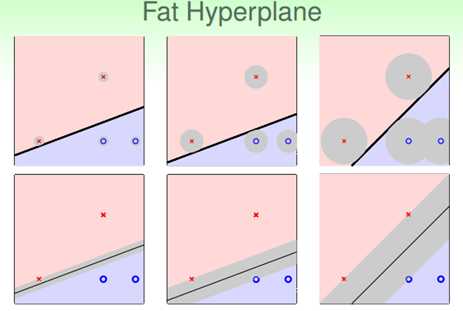
定义对W的倾向性:
对于这些W,我们喜欢能够区分对噪声识别能力强的，如果我们定义噪声是在做训练的点上产生的高斯分布的话，那么我们可以把这种倾向性定义出来，W一方面要把这两种点区分开来，另一方面要使得训练得到直线与最近的点的距离尽可能大（从图像上看就是在两类点尽可能中间的样子）。直线跟最近的点的距离称为margin(W)。
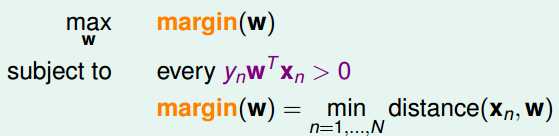
具体处理的时候把W0从W中取出来，把1从X中还原出来，从而h(x)可以表示如下:
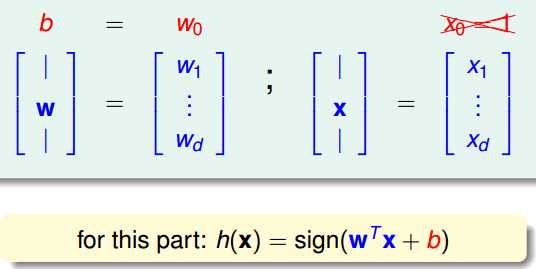这样式子中之前吸收的常数项就又回来了。
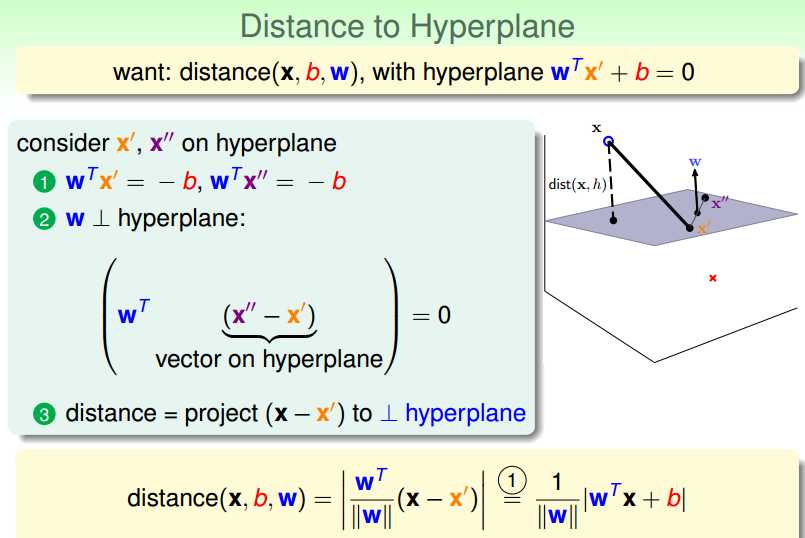
对于w和b在坐标空间所形成的超平面。那么空间上某个点到该空间的距离可以表示成上图3表达式。证明过程：假设X’,X’’是该平面上的任意两个点，那么就有表达式1，有1推出表达式2，所以w是垂直于该平面的向量，那么该空间中任意的点x跟平面上某点组成的向量(X-X’)往w向量上的投影就是X跟该平面的距离。
接下去对继续对式子做简化，首先分类直线能对两种类型的点进行正确的分类，所以满足
其次，由于Yn=+1或者-1,所以
来代替，所以目前的约束条件可以用上图最后一个式子来表示
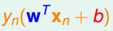
接下去我们继续进行式子的化简，我们可以假设
那么
其中m是个正实数，这里我们注意到对
进行放缩处理的话不会改变直线的形状，那么不妨将m定为1，于是有
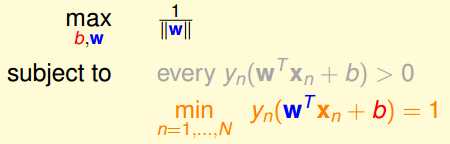
在这里表达式中every的条件也自动满足了，最后我们再将
这个式子转化为
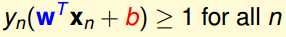
这里可以用反证法得出当满足上述式子的时候，我们肯定可以找到一组w,b,使得最小的值等于1.因此得到化简之后的式子
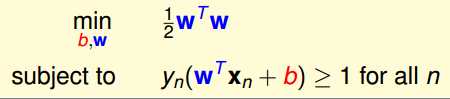
在这里，我们将第一个求最大变成了最小，因为做了取倒数的转换。因此，这里就将原来的问题转换成了一个典型的最优化问题，剩下的就是利用二次优化的Solver去解最后的w和b。
在这里需要强调的是，线性SVM解决的问题是一个Hard-Margin的问题，其要求是一定有直线可以将两类点完全区分开来，其次要求是Xn的线性组合，如果我们需要加入非线性因素的话，可以将Xn的高阶项加进来。
最有讲讲为什么要采用large-margin的约束条件来进行求解。这里将SVM跟之前L2的方法进行对比，L2中，我们对w的模进行了约束，然后去求解最小的Ein.而这里我们在满足Ein=0的情况下去求解最小的w。
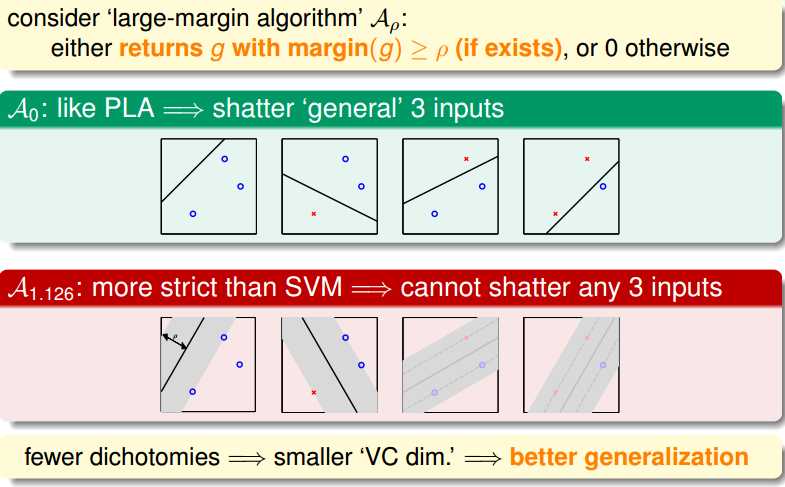
从另一种角度看过去，这里我们对margin的大小进行了要求，所以变相地减少了VC dimension，如果要求margin = 0，那么如果是三个点的情况下，要四条线可以对不同情况的这三个点进行shatter。但是margin>0的情况下，原本可以分隔两类点的直线就不能对三个点进行分割了，所以VC dimension就下降了。
上述的式子就是说对于图片中举例的情况，VC dimension是这样的，从式子中可以看到，当所要求的margin越大，那么dvc就越小。
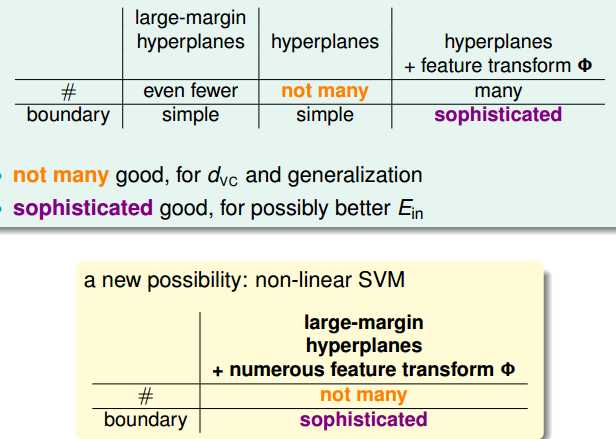
Large-Margin Hyperplanes的特点是利用少量的dvc就可以得到简单的边界，
Hyperplanes的特点就是dvc不多，但是得到的边界简单。
Hyperplanes+Fearture transform(考虑高次项)的特点是dvc变大，同时可以得到复杂的边界。
边界越复杂，那么Ein可以变小，同时如果Vc变小，可以避免Overfit。
所以接下去就考虑把上述的三点结合起来的方法。
标签：
原文地址：http://www.cnblogs.com/enzyme/p/5737041.html
