标签：
半变异函数显示测量采样点的空间自相关。绘制每对位置，然后根据这些位置拟合模型。通常使用某几个特征来描述这些模型。
查看半变异函数的模型时，您将注意到模型会在特定距离处呈现水平状态。模型首次呈现水平状态的距离称为变程。比该变程近的距离分隔的样本位置与空间自相关，而距离远于该变程的样本位置不与空间自相关。
半变异函数模型在变程处所获得的值（y 轴上的值）称为基台。偏基台等于基台减去块金。
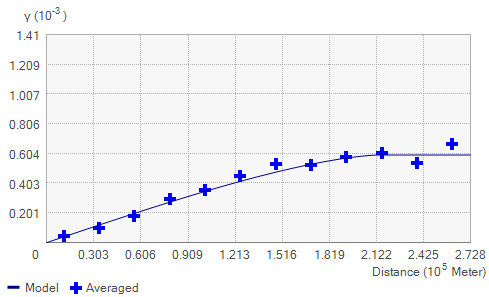半变异函数示例
从理论上讲，在零间距（步长 = 0）处，半变异函数的值是 0。但是，在极小的间距处，半变异函数通常显示块金效应，即值大于 0。例如，如果半变异函数模型在 y 轴上的截距为 2，则块金为 2。
块金效应可以归因于测量误差或小于采样间隔距离处的空间变化源（或两者）。由于测量设备中存在固有误差，因此会出现测量误差。自然现象可随着比例范围变化而产生空间变化。小于样本距离的微刻度变化将表现为块金效应的一部分。收集数据之前，能够理解空间变化的比例非常重要。
The semivariogram depicts the spatial autocorrelation of the measured sample points. Once each pair of locations is plotted, a model is fit through them. There are certain characteristics that are commonly used to describe these models.
When you look at the model of a semivariogram, you‘ll notice that at a certain distance, the model levels out. The distance where the model first flattens out is known as the range. Sample locations separated by distances closer than the range are spatially autocorrelated, whereas locations farther apart than the range are not.
The value that the semivariogram model attains at the range (the value on the y-axis) is called the sill. The partial sill is the sill minus the nugget.
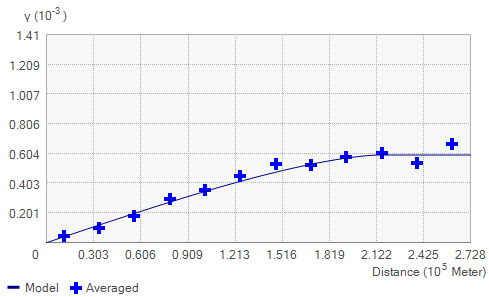Semivariogram example
Theoretically, at zero separation distance (lag = 0), the semivariogram value is 0. However, at an infinitesimally small separation distance, the semivariogram often exhibits a nugget effect, which is some value greater than 0. For example, if the semivariogram model intercepts the y-axis at 2, then the nugget is 2.
The nugget effect can be attributed to measurement errors or spatial sources of variation at distances smaller than the sampling interval or both. Measurement error occurs because of the error inherent in measuring devices. Natural phenomena can vary spatially over a range of scales. Variation at microscales smaller than the sampling distances will appear as part of the nugget effect. Before collecting data, it is important to gain some understanding of the scales of spatial variation.
标签：
原文地址：http://www.cnblogs.com/sddai/p/5742657.html
