标签:
今天我要介绍的是快速求幂模,在开始介绍之前,我们先看看如何快速求幂。这里我要介绍的是二分求幂。
二分求幂的原理如下:
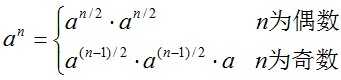
下面,我们将这个公式转换成代码:

int cifang(int a,int n)//返回值是a的n次方 { int res=1;//任何数的0次方都等于1,所以初始化为1 while(n != 0) { if(n%2 == 1)//如果n是奇数 res *= a;//就要多乘一次,即res = res*a; a = a*a; n /= 2;//二分,即n = n/2 } return res; }
我们都知道计算机是采用二进制计算的,所以如果我们采用二进制计算势必会更快。所以我们可以将上面的代码稍作改动,使用位运算。这里简单介绍一下下面代码使用到的位运算符,便于理解。
&的用法:1 & 1 = 1;1 & 0 = 0;0 & 1 = 0;0 & 0 = 0。
>>的用法:>>表示右移,n>>1:表示n除以21
还有其他的位运算符这里不再详细介绍,有兴趣的可以参见http://baike.baidu.com/view/379209.htm
下面看看代码如何修改:

int cifang(int a,int n)//返回值是a的n次方 { int res=1;//任何数的0次方都等于1,所以初始化为1 while(n != 0) { if(n&1)//如果n是奇数 res *= a;//就要多乘一次,即res = res*a; a = a*a; n >>= 1;//二分,即n = n/2 } return res; }
那如何快速求幂模呢?先给这么一个公式:(a*b)%p = ( (a%p) * (b%p) ) % p
接下来就不难实现快速求幂模了,下面直接给出代码:

int mimo(int a,int n,int b)//返回值是a的n次方对b取余后的值 { int res=1; a = a%b;//积的取余等于取余的积取余 while(n>0) { if(n & 1) //是否为奇数 res = res*a%b;//n是奇数的话就要多乘一次,原理和前面的二分求幂一样 n >>= 1;//二分,即n = n/2 a = a*a%b;//积的取余等于取余的积取余 } return res; }
标签:
原文地址:http://www.cnblogs.com/Muia/p/5743495.html