判断两个线段是否相交

标签：

我们的问题是这样的：给定一条线段的起点为$A_1$、终点为$A_2$，另一条线段的起点为$B_1$、终点为$B_2$，问线段$A_1A_2$和线段$B_1B_2$是否相交？

我们首先解释一下，两条线段相交的概念是指，存在一个点，这个点同时在两条线段上。

方法一（解方程法）：

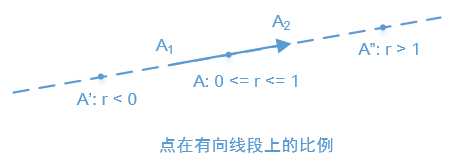
容易知道，线段$A_1A_2$上的点的集合为$A = A_1 * (1 - r_1) + A_2 * r_1$，其中$r_1 \in [0, 1]$；同理，线段$B_1B_2$上的点的集合为$B = B_1 * (1 - r_2) + B_2 * r_2$，其中$r_2 \in [0, 1]$。一般的，如果不对$r_1$（或$r_2$）的范围作约束，得到的点集构成该线段所在的直线。那么这个问题就简单了，我们可以首先将两条线段延展成直线，求出两条直线的交点，根据交点位置可以分别求出$r_1$和$r_2$，然后判断$r_1$和$r_2$是否同时在$[0, 1]$区间即可。我们把$r_1$（$r_2$）叫做点$A$（$B$）在线段$A_1A_2$（线段$B_1B_2$）上的比例。

两直线的交点满足$A_1 * (1 - r_1) + A_2 * r_1 = B_1 * (1 - r_2) + B_2 * r_2$，稍微变形可得$(A_2 - A_1) * r_1 - (B_2 - B_1) * r_2 = B_1 - A_1$，即$$\overrightarrow{A_1A_2} * r_1 - \overrightarrow{B_1B_2} * r_2 = \overrightarrow{A_1B_1}$$，表示为向量矩阵的形式为（令$\overrightarrow{r} = (r_1, r_2)^T$）：$$[\overrightarrow{A_1A_2}, - \overrightarrow{B_1B_2}] * \overrightarrow{r} = \overrightarrow{A_1B_1}$$

我们的目的是根据以上二元方程组求出$r_1$和$r_2$，但是在此之前，我们要判断一些特殊情况：

(1). 如果$\overrightarrow{A_1A_2} = \overrightarrow{0}$，即线段$A_1A_2$是一个点，这时，等式退化为$- \overrightarrow{B_1B_2} * r_2 = \overrightarrow{A_1B_1}$，两个方程一个未知量，如果有解，则点$A_1$（或$A_2$）在线段$B_1B_2$上，即两“线段”相交；否则，不相交。

(2). 如果$\overrightarrow{B_1B_2} = \overrightarrow{0}$，即线段$B_1B_2$是一个点，这时，等式退化为$\overrightarrow{A_1A_2} * r_1 = \overrightarrow{A_1B_1}$，两个方程一个未知量，如果有解，则点$B_1$（或$B_2$）在线段$A_1A_2$上，即两“线段”相交；否则，不相交。

(3). 除以上两种情况以外，如果两直线平行即$\overrightarrow{A_1A_2} // \overrightarrow{B_1B_2}$，这时要分两种情况，如果两线段平行且有平行距离，则不相交；否则，两线段在同一直线上，这时又分两种情况，两线段是否有重合部分，如果有则相交，如果没有则不相交。至于如何判断在同一直线上的两条线段是否有重合部分，可以利用快速排斥实验，后面还会讲到。

(4). 除以上三种情况外，矩阵$[\overrightarrow{A_1A_2}, - \overrightarrow{B_1B_2}]$可逆，我们可以直接求出$r_1$和$r_2$，然后判断$r_1$和$r_2$是否同时在$[0, 1]$区间即可。

方法二（外积法）：

 可以看到，解方程法需要判断几种特殊情况，而且涉及到除法运算，在计算机实现时对调用频率比价高、效率要求比较高的场景也不够“完美”。下面介绍一种基于向量外积的方法，判断逻辑更简洁，而且也不涉及除法操作。

向量外积：

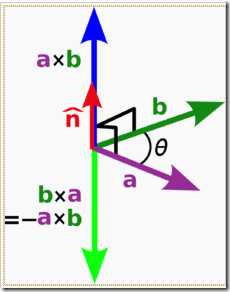
首先简单介绍一下向量外积。向量外积，也叫向量叉乘。与内积不同的是，向量外积的结果还是一个向量，它的模为两个向量围成的平行四边形的面积，方向与平行四边形所在的平面垂直，指向由右手螺旋定则确定。写成公式为：

$$\left | \overrightarrow{a} \times \overrightarrow{b} \right | = \left | \overrightarrow{a} \right | \bullet \left | \overrightarrow{b} \right | \bullet sin \theta $$

其中，$\theta$为两个向量的夹角。

如果知道两个向量的坐标$\overrightarrow{a} = (a_x, a_y, a_z)$、$\overrightarrow{b} = (b_x, b_y, b_z)$，则两个向量的外积的坐标运算为：

$$\overrightarrow{a} \times \overrightarrow{b} = (a_yb_z - a_zb_y) \overrightarrow{i} + (a_zb_x - a_xb_z)\overrightarrow{j} + (a_xb_y - a_yb_x)\overrightarrow{k}$$

为了便于记忆，还可以写为三阶行列式的形式：

$$\overrightarrow{a} \times \overrightarrow{b} = det \left | \begin{array}{cc} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{array} \right |$$

利用外积判断点与线段的相对位置：

假设有向线段为$\overrightarrow{AB}$，点为$C$，首先计算外积$\overrightarrow{AC} \times \overrightarrow{AB} = (\overrightarrow{AC}_x \cdot \overrightarrow{AB}_y - \overrightarrow{AC}_y \cdot \overrightarrow{AB}_x)\overrightarrow{k}$ （因为有$\overrightarrow{AB}_z = 0 $、$\overrightarrow{AC}_z = 0 $）。根据右手螺旋定则，如果$\overrightarrow{k}$的系数为正数，说明点C在线段AB的右侧；如果为负数，说明点C在线段AB的左侧；如果为0，说明点C在线段AB所在的直线上。写成伪代码为：

double cross(Point A, Point B, Point C) {
    double cross1 = (C.x - A.x) * (B.y - A.y);
    double cross2 = (C.y - A.y) * (B.x - A.x);
    return (cross1 - cross2);
}

线段相交判断：

回到一开始的问题，要判断线段$A_1A_2$和线段$B_1B_2$是否相交，首先计算：

T1 = cross(A1, A2, B1);
T2 = cross(A1, A2, B2);
T3 = cross(B1, B2, A1);
T4 = cross(B1, B2, A2);

根据以上结果即可判断两条线段的相交关系：

(1). 如果(T1 * T2) > 0) || (T3 * T4) > 0，说明一条线段的两个端点在另一条线段的同侧，这两条线段肯定不相交。

(2). 如果T1 == 0 && T2 == 0，说明两条线段共线，是否相交还需要进一步判断。这时可以通过判断两条线段张成的矩形是否相交来判断，而两个矩形是否相交可以通过快速排斥实验来判断。快速排斥实验稍后介绍。

(3). 其他情况，两个线段一定相交。

可以看到，这种方法不需要对线段的起终点重合（线段退化为一个点）做特殊判断，也不需要对线段平行（除了共线的情况）做特殊判断。纯几何方法，逻辑更简洁。

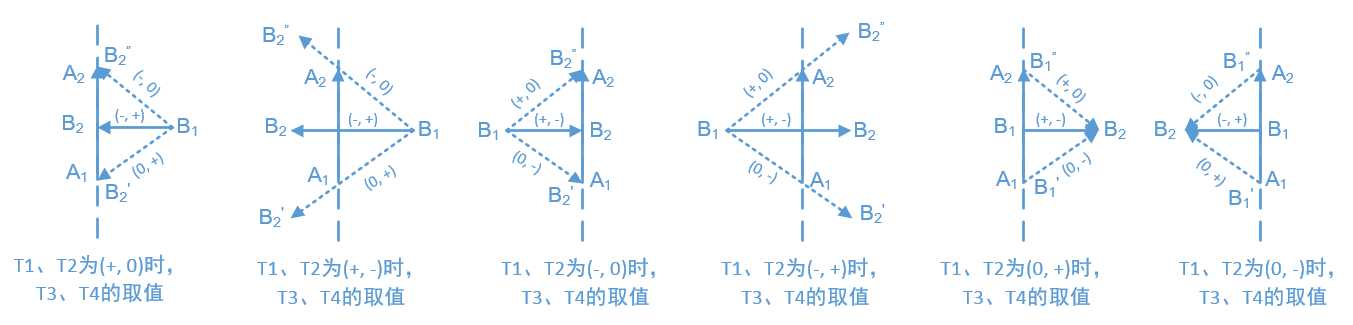
对第3种情况补充说明如下：除了第1、2种情况外（T1、T2不同号、且不同为0），T1、T2的取值还有6种情况：(+, 0)、(+, -)、(-, 0)、(-, +)、(0, +)、(0, -)。当T1、T2为(+, 0)时，T3、T4的取值只可能是(-, 0)、(-, +)、(0, +)，无论哪种情况，两线段都相交。当T1、T2为(+, -)时，T3、T4的取值只可能是(-, 0)、(-, +)、(0, +)，无论哪种情况，两线段都相交；当T1、T2为(-, 0)或(-, +)时，情况与前两个类似。当T1、T2为(0, +)时，T3、T4的取值只可能是(0, -)、(+, -)、(+, 0)，无论哪种情况，两线段都相交；当T1、T2为(0, -)时，与前一种情况类似。

补充：快速排斥实验

快速排斥实验用于判断两个矩形是否相交，因为是比较简单、也比较基础的方法，在这里就不详细介绍了，对原理感兴趣的可以参考http://blog.sina.com.cn/s/blog_71dbfe2e0101f7zb.html 一文。直接给出伪代码实现：

//*************************************************************************
// \brief: 	快速排斥实验，判断两个线段张成的矩形区域是否相交。
// \Param: 	Point S1 第一条线段的起点。
// \Param: 	Point E1 第一条线段的终点。
// \Param: 	Point S2 第二条线段的起点。
// \Param: 	Point E2 第二条线段的终点。
// \Returns: 	bool 两个线段张成的矩形区域是否相交。具有对称性，即交换两条线段（参数S1与S2交换、E1与E2交换），结果不变。
//*************************************************************************
bool rectsIntersect(Point S1, Point E1, Point S2, Point E2) {
　　if (Gmin(S1.y, E1.y) <= Gmax(S2.y, E2.y) &&
        Gmax(S1.y, E1.y) >= Gmin(S2.y, E2.y) &&
        Gmin(S1.x, E1.x) <= Gmax(S2.x, E2.x) &&
        Gmax(S1.x, E1.x) >= Gmin(S2.x, E2.x)) {
            return true;
    }
    return false;
}

因此，判断两条线段相交的伪代码为：

bool segmentsIntersect(Point A1, Point A2, Point B1, Point B2) {
    double T1 = cross(A1, A2, B1);
    double T2 = cross(A1, A2, B2);
    double T3 = cross(B1, B2, A1);
    double T4 = cross(B1, B2, A2);
　　if (((T1 * T2) > 0) || ((T3 * T4) > 0)) {   // 一条线段的两个端点在另一条线段的同侧，不相交。
        return false;
    } else if(T1 == 0 && T2 == 0) {             // 两条线段共线，利用快速排斥实验进一步判断。
        return rectsIntersect(A1, A2, B1, B2);
    } else {                                    // 其它情况，两条线段相交。
        return true;
    }
}

此文完。

判断两个线段是否相交

标签：

原文地址：http://www.cnblogs.com/kane1990/p/5742830.html