SVM4TS （SVM for Time Series） 企业级SVM大数据算法运算平台

 

1.0、什么是支持向量机SVM

    分类作为数据挖掘领域中一项非常重要的任务，它的目的是学会一个分类函数或分类模型(或者叫做分类器)，而支持向量机本身便是一种监督式学习的方法(至于具体什么是监督学习与非监督学习，请参见此系列Machine L&Data Mining第一篇)，它广泛的应用于统计分类以及回归分析中。

    支持向量机（SVM）是90年代中期发展起来的基于统计学习理论的一种机器学习方法，通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。

    通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

    对于不想深究SVM原理的同学或比如就只想看看SVM是干嘛的，那么，了解到这里便足够了，不需上层。而对于那些喜欢深入研究一个东西的同学，甚至究其本质的，咱们则还有很长的一段路要走，万里长征，咱们开始迈第一步吧，相信你能走完。

1.1、线性分类

    OK，在讲SVM之前，咱们必须先弄清楚一个概念：线性分类器(也可以叫做感知机，这里的机表示的是一种算法，本文第三部分、证明SVM中会详细阐述)。

1.1.1、分类标准

    这里我们考虑的是一个两类的分类问题，数据点用 x 来表示，这是一个 n 维向量，w^T中的T代表转置，而类别用 y 来表示，可以取 1 或者 -1 ，分别代表两个不同的类。一个线性分类器的学习目标就是要在 n 维的数据空间中找到一个分类超平面，其方程可以表示为：

                                                           

    上面给出了线性分类的定义描述，但或许读者没有想过：为何用y取1 或者 -1来表示两个不同的类别呢？其实，这个1或-1的分类标准起源于logistic回归，为了完整和过渡的自然性，咱们就再来看看这个logistic回归。

1.1.2、1或-1分类标准的起源：logistic回归

 

 

 

 

 

 

1.1.3、形式化标示

1.2、线性分类的一个例子

    下面举个简单的例子，一个二维平面(一个超平面，在二维空间中的例子就是一条直线)，如下图所示，平面上有两种不同的点，分别用两种不同的颜色表示，一种为红颜色的点，另一种则为蓝颜色的点，红颜色的线表示一个可行的超平面。

    从上图中我们可以看出，这条红颜色的线把红颜色的点和蓝颜色的点分开来了。而这条红颜色的线就是我们上面所说的超平面，也就是说，这个所谓的超平面的的确确便把这两种不同颜色的数据点分隔开来，在超平面一边的数据点所对应的 y 全是 -1 ，而在另一边全是 1 。

    接着，我们可以令分类函数（提醒：下文很大篇幅都在讨论着这个分类函数）：

  

    显然，如果 f(x)=0 ，那么 x 是位于超平面上的点。我们不妨要求对于所有满足 f(x)<</span>0 的点，其对应的 y 等于 -1 ，而 f(x)>0 则对应 y=1 的数据点。

    注：上图中，定义特征到结果的输出函数，与我们之前定义的实质是一样的。为什么？因为无论是，还是，不影响最终优化结果。下文你将看到，当我们转化到优化的时候，为了求解方便，会把yf(x)令为1，即yf(x)是y(w^x + b)，还是y(w^x - b)，对我们要优化的式子max1/||w||已无影响。

    （有一朋友飞狗来自Mare_Desiderii，看了上面的定义之后，问道：请教一下SVM functional margin 为=y(wTx+b)=yf(x)中的Y是只取1和-1 吗？y的唯一作用就是确保functional margin的非负性？真是这样的么？当然不是，详情请见本文评论下第43楼）

    当然，有些时候，或者说大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在(不过关于如何处理这样的问题我们后面会讲)，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。
    更进一步，我们在进行分类的时候，将数据点 x代入 f(x) 中，如果得到的结果小于 0 ，则赋予其类别 -1 ，如果大于 0 则赋予类别 1 。如果 f(x)=0，则很难办了，分到哪一类都不是。

   请读者注意，下面的篇幅将按下述3点走：

1. 咱们就要确定上述分类函数f(x) = w.x + b（w.x表示w与x的内积）中的两个参数w和b，通俗理解的话w是法向量，b是截距（再次说明：定义特征到结果的输出函数，与我们最开始定义的实质是一样的）；
2. 那如何确定w和b呢？答案是寻找两条边界端或极端划分直线中间的最大间隔（之所以要寻最大间隔是为了能更好的划分不同类的点，下文你将看到：为寻最大间隔，导出1/2||w||^2，继而引入拉格朗日函数和对偶变量a，化为对单一因数对偶变量a的求解，当然，这是后话），从而确定最终的最大间隔分类超平面hyper plane和分类函数；
3. 进而把寻求分类函数f(x) = w.x + b的问题转化为对w，b的最优化问题，最终化为对偶因子的求解。

    总结成一句话即是：从最大间隔出发（目的本就是为了确定法向量w），转化为求对变量w和b的凸二次规划问题。亦或如下图所示（有点需要注意，如读者@酱爆小八爪所说：从最大分类间隔开始，就一直是凸优化问题）：

 

1.3、函数间隔Functional margin与几何间隔Geometrical margin 

    一般而言，一个点距离超平面的远近可以表示为分类预测的确信或准确程度。

• 在超平面w*x+b=0确定的情况下，|w*x+b|能够相对的表示点x到距离超平面的远近，而w*x+b的符号与类标记y的符号是否一致表示分类是否正确，所以，可以用量y*(w*x+b)的正负性来判定或表示分类的正确性和确信度。

    于此，我们便引出了定义样本到分类间隔距离的函数间隔functional margin的概念。

 

1.3.1、函数间隔Functional margin

    我们定义函数间隔functional margin 为： 

      接着，我们定义超平面(w，b)关于训练数据集T的函数间隔为超平面(w，b)关于T中所有样本点(xi，yi)的函数间隔最小值，其中，x是特征，y是结果标签，i表示第i个样本，有：

  = mini  (i=1，...n)

    然与此同时，问题就出来了。上述定义的函数间隔虽然可以表示分类预测的正确性和确信度，但在选择分类超平面时，只有函数间隔还远远不够，因为如果成比例的改变w和b，如将他们改变为2w和2b，虽然此时超平面没有改变，但函数间隔的值f(x)却变成了原来的2倍。

    其实，我们可以对法向量w加些约束条件，使其表面上看起来规范化，如此，我们很快又将引出真正定义点到超平面的距离--几何间隔geometrical margin的概念（很快你将看到，几何间隔就是函数间隔除以个||w||，即yf(x) / ||w||）。

1.3.2、点到超平面的距离定义：几何间隔Geometrical margin

 

 

    在给出几何间隔的定义之前，咱们首先来看下，如上图所示，对于一个点 x ，令其垂直投影到超平面上的对应的为 x0 ，由于 w 是垂直于超平面的一个向量，为样本x到分类间隔的距离，我们有

               （||w||表示的是范数，关于范数的概念参见这里）

    又由于 x0 是超平面上的点，满足 f(x0)=0 ，代入超平面的方程即可算出： 

γ

 

（有的书上会写成把||w|| 分开相除的形式，如本文参考文献及推荐阅读条目11，其中，||w||为w的二阶泛数）

   不过这里的是带符号的，我们需要的只是它的绝对值，因此类似地，也乘上对应的类别 y即可，因此实际上我们定义 几何间隔geometrical margin 为(注：别忘了，上面的定义，=y(wTx+b)=yf(x) )：

     （代人相关式子可以得出：yi*(w/||w|| + b/||w||)）

    正如本文评论下读者popol1991留言：函数间隔y*(wx+b)=y*f(x)实际上就是|f(x)|，只是人为定义的一个间隔度量；而几何间隔|f(x)|/||w||才是直观上的点到超平面距离。

    想想二维空间里的点到直线公式：假设一条直线的方程为ax+by+c=0,点P的坐标是(x0,y0)，则点到直线距离为|ax0+by0+c|/sqrt(a^2+b^2)。如下图所示：
                                 
    那么如果用向量表示，设w=(a,b),f(x)=wx+c,那么这个距离正是|f(p)|/||w||。

1.4、最大间隔分类器Maximum Margin Classifier的定义

    于此，我们已经很明显的看出，函数间隔functional margin 和 几何间隔geometrical margin 相差一个的缩放因子。按照我们前面的分析，对一个数据点进行分类，当它的 margin 越大的时候，分类的 confidence 越大。对于一个包含 n 个点的数据集，我们可以很自然地定义它的 margin 为所有这 n 个点的 margin 值中最小的那个。于是，为了使得分类的 confidence 高，我们希望所选择的超平面hyper plane 能够最大化这个 margin 值。

    通过上节，我们已经知道：

1、functional margin 明显是不太适合用来最大化的一个量，因为在 hyper plane 固定以后，我们可以等比例地缩放 w 的长度和 b 的值，这样可以使得的值任意大，亦即 functional margin可以在 hyper plane 保持不变的情况下被取得任意大，

2、而 geometrical margin 则没有这个问题，因为除上了这个分母，所以缩放 w 和 b 的时候的值是不会改变的，它只随着 hyper plane 的变动而变动，因此，这是更加合适的一个 margin 。

    这样一来，我们的 maximum margin classifier 的目标函数可以定义为：

 

    当然，还需要满足一些条件，根据 margin 的定义，我们有

 

    其中 (等价于=  /||w||，故有稍后的  =1 时，  = 1 / ||w||)，处于方便推导和优化的目的，我们可以令=1(对目标函数的优化没有影响，至于为什么，请见本文评论下第42楼回复) ，此时，上述的目标函数转化为(其中，s.t.，即subject to的意思，它导出的是约束条件)：

 

    通过求解这个问题，我们就可以找到一个 margin 最大的 classifier ，如下图所示，中间的红色线条是 Optimal Hyper Plane ，另外两条线到红线的距离都是等于的(便是上文所定义的geometrical margin，当令=1时，便为1/||w||，而我们上面得到的目标函数便是在相应的约束条件下，要最大化这个1/||w||值)：

    通过最大化 margin ，我们使得该分类器对数据进行分类时具有了最大的 confidence，从而设计决策最优分类超平面。

1.5、到底什么是Support Vector

    上节，我们介绍了Maximum Margin Classifier，但并没有具体阐述到底什么是Support Vector，本节，咱们来重点阐述这个概念。咱们不妨先来回忆一下上节1.4节最后一张图：

 

 

    可以看到两个支撑着中间的 gap 的超平面，它们到中间的纯红线separating hyper plane 的距离相等，即我们所能得到的最大的 geometrical margin，而“支撑”这两个超平面的必定会有一些点，而这些“支撑”的点便叫做支持向量Support Vector。

   或亦可看下来自此PPT中的一张图，Support Vector便是那蓝色虚线和粉红色虚线上的点：

 

    很显然，由于这些 supporting vector 刚好在边界上，所以它们满足（还记得我们把 functional margin 定为 1 了吗？上节中：“处于方便推导和优化的目的，我们可以令=1”），而对于所有不是支持向量的点，也就是在“阵地后方”的点，则显然有。当然，除了从几何直观上之外，支持向量的概念也可以从下文优化过程的推导中得到。

    OK，到此为止，算是了解到了SVM的第一层，对于那些只关心怎么用SVM的朋友便已足够，不必再更进一层深究其更深的原理。

 

第二层、深入SVM

2.1、从线性可分到线性不可分

2.1.1、从原始问题到对偶问题的求解

    虽然上文1.4节给出了目标函数，却没有讲怎么来求解。现在就让我们来处理这个问题。回忆一下之前得到的目标函数（subject to导出的则是约束条件）：

 

 

 

 

1. 转化到这个形式后，我们的问题成为了一个凸优化问题，或者更具体的说，因为现在的目标函数是二次的，约束条件是线性的，所以它是一个凸二次规划问题。这个问题可以用任何现成的 QP (Quadratic Programming) 的优化包进行求解，归结为一句话即是：在一定的约束条件下，目标最优，损失最小；
2. 但虽然这个问题确实是一个标准的 QP 问题，但是它也有它的特殊结构，通过 Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题之后，可以找到一种更加有效的方法来进行求解，而且通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。

    也就说，除了用解决QP问题的常规方法之外，还可以通过求解对偶问题得到最优解，这就是线性可分条件下支持向量机的对偶算法，这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题。

    至于上述提到，关于什么是Lagrange duality？简单地来说，通过给每一个约束条件加上一个 Lagrange multiplier(拉格朗日乘值)，即引入拉格朗日乘子，如此我们便可以通过拉格朗日函数将约束条件融和到目标函数里去(也就是说把条件融合到一个函数里头，现在只用一个函数表达式便能清楚的表达出我们的问题)：

 

   然后我们令

 

    容易验证，当某个约束条件不满足时，例如，那么我们显然有（只要令即可）。而当所有约束条件都满足时，则有，亦即我们最初要最小化的量。因此，在要求约束条件得到满足的情况下最小化，实际上等价于直接最小化（当然，这里也有约束条件，就是≥0,i=1,…,n）   ，因为如果约束条件没有得到满足，会等于无穷大，自然不会是我们所要求的最小值。具体写出来，我们现在的目标函数变成了：

 

    这里用表示这个问题的最优值，这个问题和我们最初的问题是等价的。不过，现在我们来把最小和最大的位置交换一下（稍后，你将看到，当下面式子满足了一定的条件之后，这个式子d 便是上式P 的对偶形式表示）：

 

    当然，交换以后的问题不再等价于原问题，这个新问题的最优值用来表示。并且，我们有≤ ，这在直观上也不难理解，最大值中最小的一个总也比最小值中最大的一个要大吧！  总之，第二个问题的最优值在这里提供了一个第一个问题的最优值的一个下界，在满足某些条件的情况下，这两者相等，这个时候我们就可以通过求解第二个问题来间接地求解第一个问题。

    也就是说，下面我们将先求L 对w、b的极小，再求L 对的极大。而且，之所以从minmax的原始问题，转化为maxmin的对偶问题，一者因为是的近似解，二者，转化为对偶问题后，更容易求解。

2.1.2、KKT条件

    与此同时，上段说“在满足某些条件的情况下”，这所谓的“满足某些条件”就是要满足KKT条件。那KKT条件的表现形式是什么呢？据维基百科：KKT 条件的介绍，一般地，一个最优化数学模型能够表示成下列标准形式：

 

 

    其中，f(x)是需要最小化的函数，h(x)是等式约束，g(x)是不等式约束，p和q分别为等式约束和不等式约束的数量。同时，我们得明白以下两个定理：

 

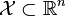• 凸优化的概念： 为一凸集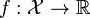，  为一凸函数。凸优化就是要找出一点  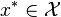，使得每一  满足  。
• KKT条件的意义：它是一个非线性规划（Nonlinear Programming）问题能有最优化解法的必要和充分条件。

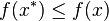    那到底什么是所谓Karush-Kuhn-Tucker条件呢？KKT条件就是指上面最优化数学模型的标准形式中的最小点 x* 必须满足下面的条件：

 

    经过论证，我们这里的问题是满足 KKT 条件的（首先已经满足Slater condition，再者f和gi也都是可微的，即L对w和b都可导），因此现在我们便转化为求解第二个问题。也就是说，现在，咱们的原问题通过满足一定的条件，已经转化成了对偶问题。而求解这个对偶学习问题，分为3个步骤，首先要让L(w，b，a) 关于 w 和 b 最小化，然后求对α的极大，最后利用SMO算法求解对偶因子。

2.1.3、对偶问题求解的3个步骤

    （1）、首先固定，要让 L 关于 w 和 b 最小化，我们分别对w，b求偏导数，即令 ∂L/∂w 和 ∂L/∂b 等于零（对w求导结果的解释请看本文评论下第45楼回复）：

 

    以上结果代回上述的 L： 

 

    得到：

 

 

    提醒：有读者可能会问上述推导过程如何而来？说实话，其具体推导过程是比较复杂的，如下图所示：

      最后，得到：

 

 

 

    如 jerrylead所说：“倒数第4步”推导到“倒数第3步”使用了线性代数的转置运算，由于ai和yi都是实数，因此转置后与自身一样。“倒数第3步”推导到“倒数第2步”使用了(a+b+c+…)(a+b+c+…)=aa+ab+ac+ba+bb+bc+…的乘法运算法则。最后一步是上一步的顺序调整。

 

    从上面的最后一个式子，我们可以看出，此时的拉格朗日函数只包含了一个变量，那就是，然后下文的第2步，求出了便能求出w，和b，由此可见，上文第1.2节提出来的核心问题：分类函数也就可以轻而易举的求出来了。

    （2）、求对的极大，即是关于对偶问题的最优化问题，从上面的式子得到：

    (不得不提醒下读者：经过上面第一个步骤的求w和b，得到的拉格朗日函数式子已经没有了变量w，b，只有，而反过来，求得的将能导出w，b的解，最终得出分离超平面和分类决策函数。为何呢？因为如果求出了，根据，即可求出w。然后通过，即可求出b )

   如前面所说，这个问题有更加高效的优化算法，即我们常说的SMO算法。

 

2.1.5、线性不可分的情况

    OK，为过渡到下节2.2节所介绍的核函数，让我们再来看看上述推导过程中得到的一些有趣的形式。首先就是关于我们的 hyper plane ，对于一个数据点 x 进行分类，实际上是通过把 x 带入到算出结果然后根据其正负号来进行类别划分的。而前面的推导中我们得到 

 

    因此分类函数为：

    这里的形式的有趣之处在于，对于新点 x的预测，只需要计算它与训练数据点的内积即可（表示向量内积），这一点至关重要，是之后使用 Kernel 进行非线性推广的基本前提。此外，所谓 Supporting Vector 也在这里显示出来——事实上，所有非Supporting Vector 所对应的系数都是等于零的，因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。

    为什么非支持向量对应的等于零呢？直观上来理解的话，就是这些“后方”的点——正如我们之前分析过的一样，对超平面是没有影响的，由于分类完全有超平面决定，所以这些无关的点并不会参与分类问题的计算，因而也就不会产生任何影响了。

    回忆一下我们2.1.1节中通过 Lagrange multiplier得到的目标函数：

 

     注意到如果 xi 是支持向量的话，上式中红颜色的部分是等于 0 的（因为支持向量的 functional margin 等于 1 ），而对于非支持向量来说，functional margin 会大于 1 ，因此红颜色部分是大于零的，而又是非负的，为了满足最大化，必须等于 0 。这也就是这些非Supporting Vector 的点的局限性。 

    从1.5节到上述所有这些东西，便得到了一个maximum margin hyper plane classifier，这就是所谓的支持向量机（Support Vector Machine）。当然，到目前为止，我们的 SVM 还比较弱，只能处理线性的情况，不过，在得到了对偶dual 形式之后，通过 Kernel 推广到非线性的情况就变成了一件非常容易的事情了(相信，你还记得本节开头所说的：“通过求解对偶问题得到最优解，这就是线性可分条件下支持向量机的对偶算法，这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题”)。

2.2、核函数Kernel

 

2.2.1、特征空间的隐式映射：核函数

 

    咱们首先给出核函数的来头：

 

• 在上文中，我们已经了解到了SVM处理线性可分的情况，而对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。由于核函数的优良品质，这样的非线性扩展在计算量上并没有比原来复杂多少，这一点是非常难得的。当然，这要归功于核方法——除了 SVM 之外，任何将计算表示为数据点的内积的方法，都可以使用核方法进行非线性扩展。

   

    现在让我们再回到 SVM 的情形，假设原始的数据时非线性的，我们通过一个映射 ?(⋅) 将其映射到一个高维空间中，数据变得线性可分了，这个时候，我们就可以使用原来的推导来进行计算，只是所有的推导现在是在新的空间，而不是原始空间中进行。当然，推导过程也并不是可以简单地直接类比的，例如，原本我们要求超平面的法向量 w ，但是如果映射之后得到的新空间的维度是无穷维的（确实会出现这样的情况，比如后面会提到的 高斯核Gaussian Kernel ），要表示一个无穷维的向量描述起来就比较麻烦。