标签:
T1 bzoj1132[POI2008]TRO
还是太弱了。。。。测试时看到这题直接懵逼,极角排序什么的根本想不起来,只会n^3暴力怎么破。。。。。。不过竟然有84。。。。。QAQ
正解是n^2logn的,首先为了避免算重,以点的x坐标为第一关键字和y坐标为第二关键字排好序,然后O(n)枚举当前点计算以当前点为三角形的一个顶点的三角形面积之和。
显然不能n^2枚举,于是想到nlogn极角排序,以当前点为原点建一个平面直角坐标系,加一个前缀和将计算优化到O(n),于是就是n^2logn的了
至于怎么前缀和优化,因为一个点j,向量ij与前面所有的向量的叉积之和就是向量ij的贡献。
然后稍微手推一下就可以得出ans+=sumx*a[j].y-sumy*a[j].x就可以O(n)了。。。。。
精度问题什么的考虑一下就好了。。。。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 #define maxn 10000 8 9 int n,tot; 10 long long sumx,sumy,ans; 11 12 struct point{ 13 int x,y; 14 double slope; 15 }a[maxn],b[maxn]; 16 17 bool cmp(point a,point b){ 18 return a.x<b.x||(a.x==b.x&&a.y<b.y); 19 } 20 21 bool cmp_slope(point a,point b){ 22 return a.slope<b.slope; 23 } 24 25 int main(){ 26 scanf("%d",&n); 27 for (int i=1;i<=n;i++) 28 scanf("%d%d",&a[i].x,&a[i].y); 29 sort(a+1,a+n+1,cmp); 30 for (int i=1;i<=n;i++){ 31 tot=0,sumx=0,sumy=0; 32 for (int j=i+1;j<=n;j++) b[++tot].slope=atan2(a[j].y-a[i].y,a[j].x-a[i].x),b[tot].x=a[j].x-a[i].x,b[tot].y=a[j].y-a[i].y; 33 sort(b+1,b+tot+1,cmp_slope); 34 for (int j=1;j<=tot;j++){ 35 ans+=sumx*b[j].y-sumy*b[j].x; 36 sumx+=b[j].x,sumy+=b[j].y; 37 } 38 } 39 printf("%lld.%d",ans>>1,(ans&1)?5:0); 40 return 0; 41 }
T2 bzoj1038[ZJOI2008]瞭望塔
测试时看到这题认为最可写,于是码了1h+杂技写法,以为用一个单调栈维护斜率什么的搞一搞就行了,然而并没有看到瞭望塔能建在[x1,xn]的任意位置。。。。。
然后发现这就是一道半平面交的题,对每个拐点求出它左右最远能望到哪个点,然后连两条直线,对于所有在这条直线上方的点,它都可以看到,由于光路可逆原理,直线上方任意的点也能看到它。
然后这就是许多个半平面,求半平面交就好了。。。
然而测试时傻叉的以为半平面内y最小的点一定最优。。。。。于是狗带。。。。竟然还有80。。。
正解是半平面交的下凸壳可以看成分段一次函数,折线下方村落的折线也可以看成分段一次函数,然后求两段一次函数之间的最小距离,必定会在端点上而不会是直线上的某一点的距离。
因为折线可以分解为一段一段的直线,对于每一段直线,它所对应的直线斜率无论是比它大还是小,最短距离都取决于端点,平行也是一样,YY一下就会觉得它很正确。。。很显然。。。
于是上半平面交。。。

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 #define maxn 330 8 const double inf=1e10; 9 10 int n,tot,sum,head,tail; 11 double ans; 12 13 struct point{ 14 double x,y; 15 }p[20*maxn],a[20*maxn],pa[20*maxn]; 16 17 struct line{ 18 point from,to; 19 double slope; 20 }l[20*maxn],q[20*maxn]; 21 22 point operator -(point a,point b){return(point){a.x-b.x,a.y-b.y};} 23 double operator *(point a,point b){return a.x*b.y-a.y*b.x;} 24 bool operator <(line a,line b){ 25 return (a.slope==b.slope)?((a.to-a.from)*(b.to-a.from)<0):a.slope<b.slope; 26 } 27 bool operator ==(line a,line b){ 28 return a.slope==b.slope; 29 } 30 31 point getpoint(line a,line b){ 32 double t1=(a.to-a.from)*(b.to-a.from),t2=(b.from-a.from)*(a.to-a.from); 33 double t=t1/(t1+t2); 34 return (point){b.to.x+t*(b.from.x-b.to.x),b.to.y+t*(b.from.y-b.to.y)}; 35 } 36 37 bool check(line a,line b,line c){ 38 point d=getpoint(a,b); 39 return ((c.to-c.from)*(d-c.from)<0); 40 } 41 42 double find1(double x){ 43 for (int i=1;i<=n;i++) 44 if (x>=a[i].x && x<a[i+1].x){ 45 line tmp1,tmp2; 46 tmp1.from=(point){x,0},tmp1.to=(point){x,max(a[i].y,a[i+1].y)}; 47 tmp2.from=(point){a[i].x,a[i].y},tmp2.to=(point){a[i+1].x,a[i+1].y}; 48 point ttt=getpoint(tmp1,tmp2); 49 return ttt.y; 50 } 51 return a[n].y; 52 } 53 54 double find2(double x){ 55 for (int i=head;i<=tail;i++) 56 if (x>=q[i].from.x && x<=q[i].to.x){ 57 line tmp; 58 tmp.from=(point){x,0},tmp.to=(point){x,max(q[i].from.y,q[i].to.y)}; 59 point ttt=getpoint(tmp,q[i]); 60 return ttt.y; 61 } 62 } 63 64 void solve(){ 65 head=1,tail=2; 66 q[1]=l[1],q[2]=l[2]; 67 for (int i=3;i<=sum;i++){ 68 while (head<tail && check(q[tail-1],q[tail],l[i])) tail--; 69 while (head<tail && check(q[head+1],q[head],l[i])) head++; 70 q[++tail]=l[i]; 71 } 72 while (head<tail && check(q[tail-1],q[tail],q[head])) tail--; 73 while (head<tail && check(q[head+1],q[head],q[tail])) head++; 74 q[tail+1]=q[head]; 75 for (int i=head;i<=tail;i++){ 76 point t=getpoint(q[i],q[i+1]); 77 q[i].to=q[i+1].from=t; 78 ans=min(ans,fabs(t.y-find1(t.x))); 79 } 80 for (int i=1;i<=n;i++) 81 ans=min(ans,fabs(a[i].y-find2(a[i].x))); 82 printf("%.3f",ans); 83 } 84 85 int main(){ 86 // freopen("input.txt","r",stdin); 87 // freopen("output.txt","w",stdout); 88 scanf("%d",&n); 89 ans=inf,inf; 90 for (int i=1;i<=n;i++) 91 scanf("%lf",&a[i].x); 92 for (int i=1;i<=n;i++) 93 scanf("%lf",&a[i].y); 94 l[++tot].from=(point){-inf,-inf},l[tot].to=(point){inf,-inf}; 95 l[++tot].from=(point){inf,inf},l[tot].to=(point){-inf,inf}; 96 for (int i=1;i<=n;i++){ 97 int k=0; 98 for (int j=i+1;j<=n;j++){ 99 if (a[j].y<=a[i].y) continue; 100 if (!k) k=j; 101 else if ((a[k]-a[i])*(a[j]-a[i])>0) k=j; 102 } 103 if (k) l[++tot].from=a[i],l[tot].to=a[k]; 104 } 105 for (int i=n;i;i--){ 106 int k=0; 107 for (int j=i-1;j;j--){ 108 if (a[j].y<=a[i].y) continue; 109 if (!k) k=j; 110 else if ((a[k]-a[i])*(a[j]-a[i])<0) k=j; 111 } 112 if (k) l[++tot].to=a[i],l[tot].from=a[k]; 113 } 114 l[++tot].from=(point){a[1].x,inf},l[tot].to=(point){a[1].x,-inf}; 115 l[++tot].from=(point){a[n].x,-inf},l[tot].to=(point){a[n].x,inf}; 116 for (int i=1;i<=tot;i++) l[i].slope=atan2(l[i].to.y-l[i].from.y,l[i].to.x-l[i].from.x); 117 sort(l+1,l+tot+1); 118 sum=unique(l+1,l+tot+1)-l; 119 sum--; 120 solve(); 121 return 0; 122 }
T3 bzoj4677 network
zy加题果然神速。。。。。
测试时由于T2打太久了,而且样例都还没过。。。。于是情急之下5分钟打了一个T3 n^2暴力,发现过了样例开心得不得了,然而手抽多打一个0,MLE。。。。。。。QAQ
这是一个类似杨辉三角的转移过程,可以发现,对于f[x][y],能够转移的p[]的区间是[y-x+1,y],含义是第只有第(y-x+1)种运输线到第y种运输线可能在转移过程中出现。
发现这是一个区间的问题,于是就立马能想到线段树。。。然后开开心心地找到区间[y-x+1,y]的最小值,然后转移,开开心心submit,然后WA。。。。。
因为对于最小值转移正确性无法保证,因为你只能保证p[k]最小,不能保证sigma(p[k+1],p[y])+p[k]最小。
于是考虑最优解的形式,因为一旦起点确定,你要往下走多少次,往右走多少次也确定了,因为对于每一条运输线都要往下走,你可以选择的是竖直向下,也可以选择斜向下,而往斜要走多少次已经确定了,为什么不在这条路径上(注意,是这条路径上)走最多次最小的k呢?
那么对于任取一起点k的最优解,一定就是如下图所示的情况
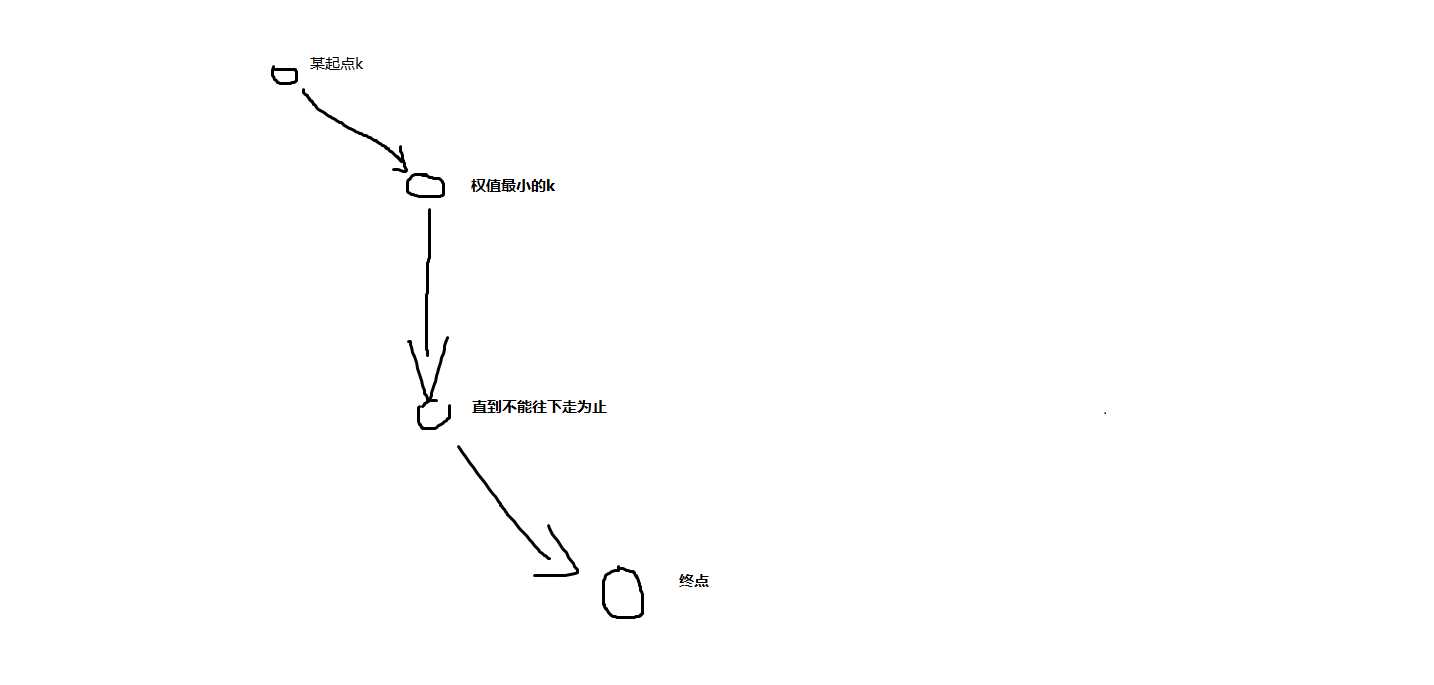
那么既然要从某k走到权值最优的k,那么为什么不直接以权值最优的k为起点呢?那么新的情况就如下图
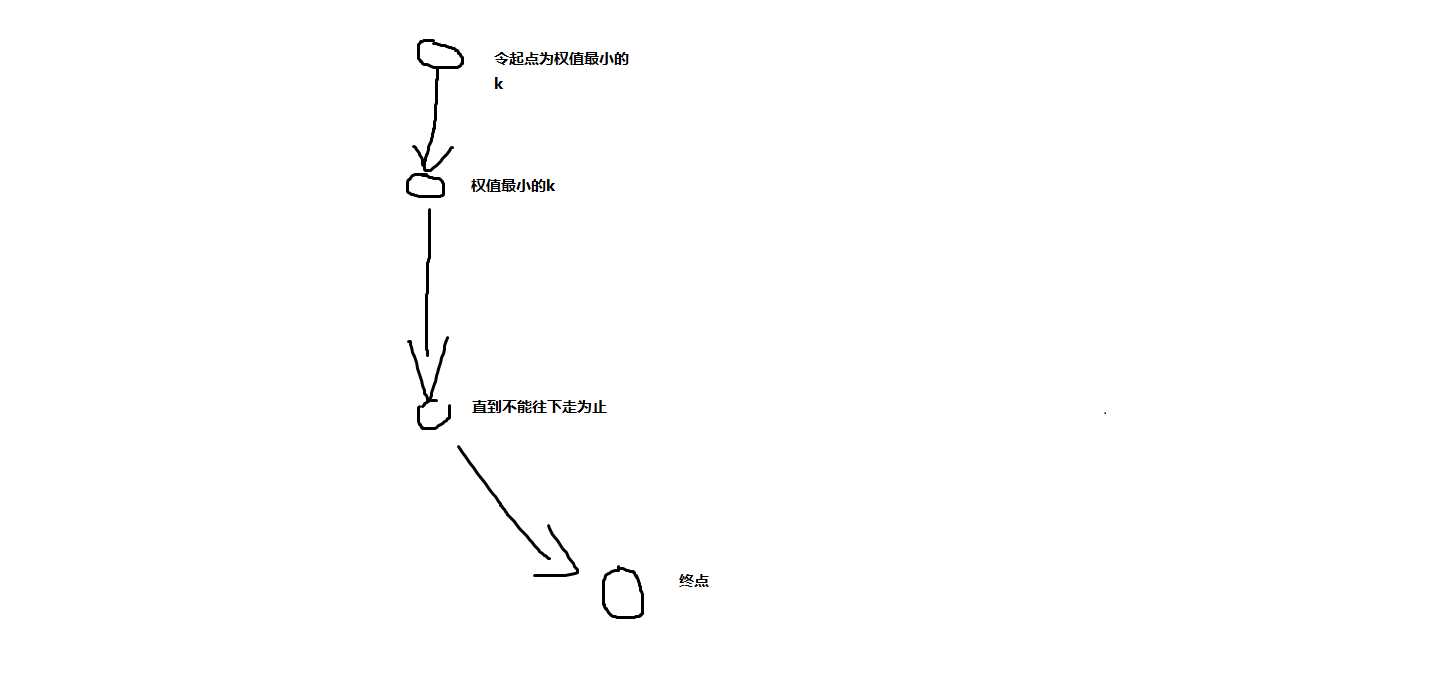
这样一来,无论如何对于这条路径也无法优化了,那么这一定就是最优解的形式。
因为如果要每次走到最优的k再不断往下走,不如选最优的k为起点,然而这也仅仅只是最优解的形式,并不能直接选取它作为最优解,而最优解的形式已经确定下来了,这就为我们解题带来了很大方便。
考虑对于每一个区间内的k,都令它直接往下走,走到不能走为止,再往左。
因为如果这个k它本身的权值是不够优的,还让它一直往下走,显然这不是以该k为起点的路径的最优解,但实际上选它作为起点的路径本就是没有意义的,因为完全可以以该路径上最优的点作为起点,因此即使该方案不够优,却不会影响到答案,因为已经确定了解的形式,且该决策本就是没有意义的。
但如果这个k足够优,那么显然如果让它一直往下走,它的决策不会比其他的方案差,所以对于能影响到答案的决策,它是最优的。
如果还是不能理解,换句话说,决策序列其实是非降的,因为对于k1<k2,还有p[k1]>p[k2],则k1一定没有k2优,而在决策序列元素l[i],l[i+1],对于它们在原来的p[]序列中中间夹的所有数p[j]都一定有p[j]>l[i] && p[j]>l[i+1](如果它能成为一个决策,那么就一定会有这样的一个性质),也就是说,如果用决策序列将原来的p[]序列分成若干块,块内的元素都是单调不升的。
而且每个块最后一个元素都要优于块内其余所有的元素。若对于每个元素的最优解显然是把它的路径先伸展到该块最后一个元素,但它们是一定没有该块最后一个元素优的,所以一路下来又有何妨。同样,每块最后一个元素无论是最优路径还是最优解形式的路径都是一样的,这也是能够更新答案的路径,它们的解都是最优的。
那么对于一个k,最优解形式就是k出现(x-y+k)次,其余[k+1,y]只出现一次。
也就是求一个min{(x-y+k)*p[k]+sigma(p[i]|(k+1<=i<=y))}
令sum[i]表示sigma(p[i]),那么就有相当于min{(x-y)*p[k]+k*p[k]-sum[k]}+sum[y]
令k=(x-y),x=p[k],y=k*p[k],即求kx+y。令kx+y=b,转化为直线令截距最小,即是用线段树维护一个上凸壳。
时间复杂度O(nlog^2n)

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 #define maxn 100010 8 #define inf 1e15 9 10 int top,n,m; 11 int p[maxn]; 12 long long ans; 13 long long sum[maxn]; 14 15 struct point{ 16 int x; 17 long long y; 18 }val[maxn],stack[maxn*20]; 19 20 point operator -(point a,point b){return(point){a.x-b.x,a.y-b.y};} 21 long long operator *(point a,point b){return a.x*b.y-a.y*b.x;} 22 23 struct segment_tree{ 24 int begin,end,size; 25 }tree[maxn<<3]; 26 27 void push(point x,int tmp){ 28 while (top>tmp && (stack[top]-stack[top-1])*(x-stack[top])<=0) top--; 29 stack[++top]=x; 30 } 31 32 void merge(int p){ 33 int lson=p<<1,rson=p<<1|1,lbeg=tree[lson].begin,rbeg=tree[rson].begin,tmp=top+1; 34 tree[p].begin=top+1; 35 while (lbeg<=tree[lson].end && rbeg<=tree[rson].end){ 36 point x; 37 if (stack[lbeg].x<stack[rbeg].x||(stack[lbeg].x==stack[rbeg].x && stack[lbeg].y<stack[rbeg].y)) x=stack[lbeg++]; 38 else x=stack[rbeg++]; 39 push(x,tmp); 40 } 41 while (lbeg<=tree[lson].end) push(stack[lbeg++],tmp); 42 while (rbeg<=tree[rson].end) push(stack[rbeg++],tmp); 43 tree[p].end=top; 44 } 45 46 void build(int p,int l,int r){ 47 if (l==r){ 48 tree[p].begin=tree[p].end=++top; 49 stack[top]=val[l]; 50 return; 51 } 52 int mid=(l+r)>>1; 53 build(p<<1,l,mid); 54 build(p<<1|1,mid+1,r); 55 merge(p); 56 } 57 58 long long calc(int p,int x,int y){return (long long)stack[p].x*(x-y)+stack[p].y+sum[y];} 59 60 void solve(int p,int x,int y){ 61 int l=tree[p].begin,r=tree[p].end; 62 while (r-l>=3){ 63 int mid=l+(r-l)/3,midmid=r-(r-l)/3; 64 if (calc(mid,x,y)<calc(midmid,x,y)) r=midmid; 65 else l=mid; 66 } 67 for (int i=l;i<=r;i++) ans=min(ans,calc(i,x,y)); 68 } 69 70 void query(int p,int l,int r,int x,int y,int tmpx,int tmpy){ 71 if (x<=l && r<=y){ 72 solve(p,tmpx,tmpy); 73 return; 74 } 75 int mid=(l+r)>>1; 76 if (x<=mid) query(p<<1,l,mid,x,y,tmpx,tmpy); 77 if (y>mid) query(p<<1|1,mid+1,r,x,y,tmpx,tmpy); 78 } 79 80 int main(){ 81 scanf("%d%d",&n,&m); 82 for (int i=1;i<=n;i++) scanf("%d",&p[i]),sum[i]=sum[i-1]+p[i],val[i]=(point){p[i],(long long)i*p[i]-sum[i]}; 83 build(1,1,n); 84 for (int i=1,x,y;i<=m;i++){ 85 scanf("%d%d",&x,&y); 86 x^=ans,y^=ans; 87 ans=inf; 88 query(1,1,n,y-x+1,y,x,y); 89 printf("%lld\n",ans); 90 } 91 return 0; 92 }
标签:
原文地址:http://www.cnblogs.com/DUXT/p/5751312.html