标签:
博弈(4)棋盘游戏
题目地址:http://acm.fafu.edu.cn/problem.php?id=1530
Description:
z和c想放松放松心情,想来玩个棋盘游戏,给你一个棋盘有n行m列的格子,有一枚五毛的硬币在(1,m)的位置。游戏规则:一、这枚硬币只能向下或者向左或者向左下45度移动一个格子;二、没法移动的人输。游戏总是由Z开始。(假设Z和C都很聪明,都用最好的策略)
Input:
输入包含多组测试数据,每组数据输入n,m两个非负整数,当n=0和m=0时,结束。(n不会超过32位)
Output:
对于每组测试数据输出一行,如果Z能赢输出“Z”,否则输出“C”。
Sample Input:
7 3
5 4
6 6
0 0
Sample Output:
C
Z
Z
题意分析:Z先从从(1,m)开始走,每次只能向左,下,左下走,谁先到左下角谁赢。
这里,我们引入必胜局面(1)和必输局面(0)。我们知道不管谁赢,当在左下角轮到他决策的时候,他已经无路可走,就像面临一个死棋的局面。那么,我们可以把左下角的状态记为0(即必输局面)。因为每次只能向左,下,左下走,所以左下角的状态与它右,上,右上的状态相反,将这3个状态都记为1(必胜局面)。下面举个例子,当n=7,m=6时,如图1:
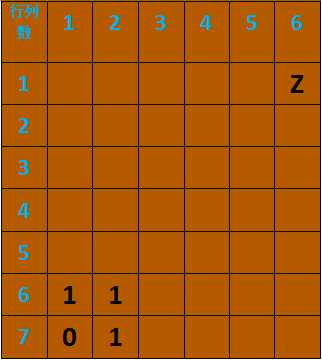
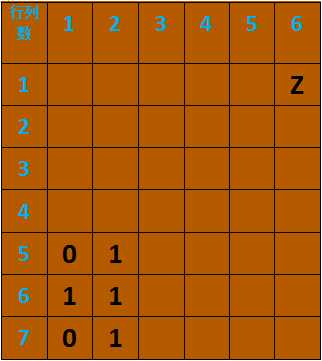
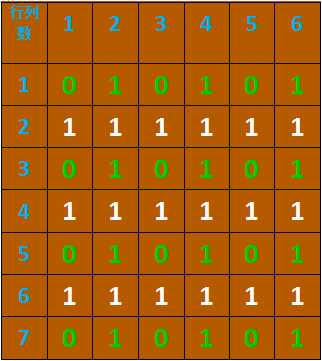
图1 图2 图3
接着我们再看,如果Z在(1,5)的时候,它只能向下走到(1,6),此时C也只能向下走到(1,7),而这时候轮到Z在(1,7)点进行决策,然而发现无路可走,所以(1,5)为0(必输局面);同样的,当Z在(2,5)的时候,它可以走到(1,5),(1,6),(2,6)但是他选最优决策(1,5),因为其它两点都会使Z输(看题目:Z和C都很聪明,都用最好的策略),而走(1,5)稳赢,所以(2,5)为1(必赢局面),如图2。其它的依次类推。当我们推出一些点后就可以发现规律,然后将整个图补齐即可。(找不到规律直接看图3,建议自己找一遍加深印象)最后,我们将(1,m)的状态打出来就可以了,最终如图3。如果状态为1,Z赢;状态为0,C赢。
总的来说,不管n和m的值为多少,我们只要将左下角记为0(即(1,n)的状态值为0),然后按规律推出(1,m)的状态值就可以解决问题。代码很容易实现,想怎么实现就怎么实现,这里就不贴出来了。
标签:
原文地址:http://www.cnblogs.com/Muia/p/5751250.html