标签:
4 5 2 2
3 361 649 676
588 992 762 156
993 169 662 34
638 89 543 525
165 254 809 280
思路:1:本来用的是直接求和从map[1][1]到map[x][y],结果真的超时了,所以还是要用DP;
2:sum的功能则是求从元素(1, 1)开始到(x, y)的总和,同样,可以求出任意一个子矩阵内的所有元素之和,即sum(x2, y2) - sum(x1-1, y2) - sum(x2, y1-1) + sum(x1-1, y1-1)
输入: map[i][j]=map[i-1][j]+p; 得下面的表
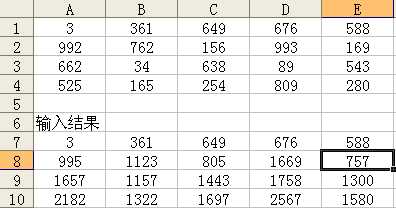
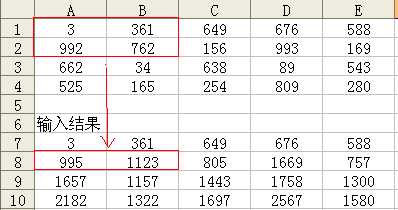
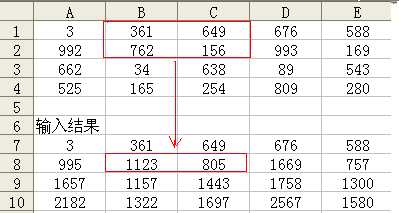


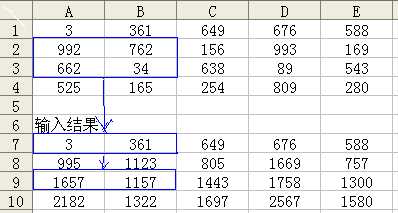
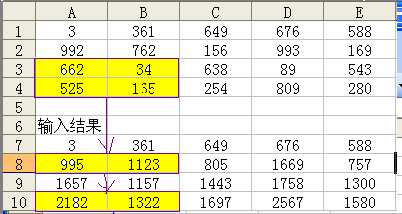
图 (4) 图(5)
AC代码:
1 #include<cstdio> 2 int m, n, x, y; 3 int map[1002][1002]={0}; 4 int sum[1002]={0}; 5 int main() 6 { 7 int p, t; 8 scanf("%d", &t); 9 while( t-- ){ 10 int i=0, j=0; 11 scanf("%d %d %d %d", &m, &n, &x, &y); 12 for(i = 1; i <= m; i++){ 13 14 for(j = 1; j <= n; j++){ 15 scanf("%d", &p); 16 map[i][j]=map[i-1][j]+p; 17 printf("%d ",map[i][j]); 18 }printf("\n");} 19 int max = 0; 20 for(i = x; i <= m; i++){ 21 //横向求矩阵的最大和 22 sum[y] = 0; 23 for(j = 1; j <= y; j++) 24 sum[y] += map[i][j] - map[i-x][j]; 25 max = max > sum[y] ? max : sum[y]; 26 //纵向求最大的矩阵和 27 for(j = y + 1; j <= n; j++){ 28 sum[j] = sum[j-1] + (map[i][j]-map[i-x][j]) - (map[i][j-y]-map[i-x][j-y]); 29 max = max > sum[j] ? max : sum[j]; 30 } 31 } 32 printf("%d\n", max); 33 } 34 return 0; 35 }
标签:
原文地址:http://www.cnblogs.com/123tang/p/5754438.html