标签：

一、矩阵消元

　　在解方程组时我们经常用到消元法，通过对方程的倍乘、加减等操作可以得到所求方程的解。既然方程组可以用消元法进行求解，那么方程组变成矩阵自然也可以使用消元法。

　　我们召唤一个方程组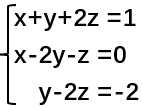 ，本来想先用方程组演示消元法的，但是方程组书写上太麻烦，所以，直接用矩阵演示了~~

　　我们拿出它的系数矩阵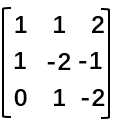

　消元的知识准备：对系数矩阵消元

　　我们保留矩阵的第一行，然后消去下方所有行的多余变量

　　先从x位置开始。

　　既然要消去x，那么我们只需要关心矩阵的第一列，如图。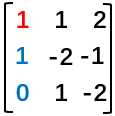

　　在图中我们可以看到，关键的位置是红色标记的1（我们将这种位置的数字称为“主元”，因为它是第一个出现的，所以叫它“主元一”），而我们的目的是将蓝色标记的位置都变成0。

　　操作很简单，第一行不变（因为它是主元行），第二行整体减去一倍的第一行，第三行不做变化（因为它本来就是0）。

　　于是我们得到了如下图的矩阵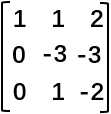，可以看到，第一列的元素除了第一行都变成了0。

　　然后，我们处理y。

　　继续观察矩阵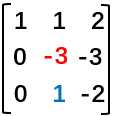

　　如今，-3是新的主元（主元二），而我们要消去的是蓝色位置的1。

　　操作依旧简单，第一、二行都不变，将第三行减去-1/3倍的第二行。

　　然后得到这样的一个矩阵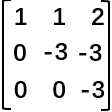。（把主元标记一下）

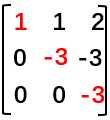　　事实上对系数矩阵的消元到这里就结束了，我们得到了一个上三角矩阵（因为它只有上半部分的三角形里有数字），我们用U表示它。

　　顺便一提，消元时主元不能为0，如果主元为0，可以将主元所在的行与它下面的主元位置非0的行进行交换（比如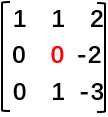 变成）。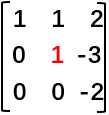

　　再顺便一提，行列式的值就是主元的乘积，所以该矩阵行列式得9

　　如果没有可以进行交换的行，方程无解，这种情况以后再讨论。

　消元的第一步：对增广矩阵消元

　　在正常的对方程组的消元过程中，等号右边的项与左边进行相同的操作，在矩阵中也是一样。

　　对于方程组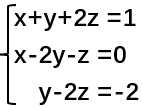，我们得到了它的系数矩阵A：，然后，我们把它等号右边的部分b：放到A中，得到一个新矩阵：

　　我们管这个新矩阵叫做“增广矩阵”，因为它相对于原矩阵增加了一列。

　　对于增广矩阵的每一行，我们作与上方系数矩阵消元相同的操作（换句话说，就是在对系数矩阵消元的过程中连带着变换增加的那一列）

　　注：正常的消元直接操作增广矩阵即可，上面对系数矩阵单独消元只是为了加深各位的理解。

　消元的第二布：回代

　　经过上面的变换，增广矩阵变成了这个样子：。

　　把它改写成方程组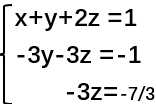

　　求解，得到x=-1/9,y=-4/9,z=7/9（WTF）

 二、消元矩阵

　　上方我们讨论了如何进行矩阵消元，现在，让我们换一种思考方式，用矩阵来表示消元的过程。

　（1）预备知识

　　之前我们曾讨论过矩阵乘向量的问题，我们的结论是：矩阵乘向量的结果实际是矩阵列的线性组合。

　　但是，矩阵消元用到的都是矩阵的行，那么，矩阵的行之间是否也有相似的性质呢？按套路来讲，如果没有这种性质我就不会问这个问题了。

　　事实上，当一个向量乘一个矩阵时，得到的结果就是该矩阵行的线性组合。

　　比如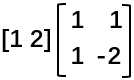，其结果相当于1*[1 1] + 2*[1 -2] = [3 -3]。

　　这里加上一些略微超前的概念：在一个矩阵A的左边乘一个矩阵，就是对A进行行变换，而在A右边乘一个矩阵，就是对A进行列变换。

　（2）用矩阵消元

　　我们依然用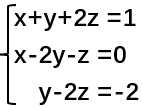这个方程进行演示，拿出它的系数矩阵A：

　　还记得我们的步骤么？

　　首先，保持第一行不变，第二行整体减去一倍的第一行，第三行同样不变。

　　总结一下，我们需要拿出-1倍的第一行，然后将它和第二行进行线性组合（相加），然后其他行不变（注意，在矩阵消元时我们是用两行相减，而“线性组合”是相加）。

 　　按照需求，我们只需要在A的左边乘上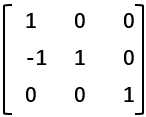（我们用E₁表示这个矩阵）

　　为什么是这个矩阵？我们一行一行地看。

　　首先，A的第一行不变，因此我们需要拿出A的1个第一行，0个第二行，0个第三行（进行线性组合），于是1 0 0组成了E₁的第一行。

　　然后，我们需要-1个A的第一行，1个第二行，0个第三行进行线性组合，所以 -1 1 0组成了E₁的第二行。

　　第三行不变，因此需要0个第一行，0个第二行，1个第三行，所以E₁的第三行是0 0 1

　　经过变换，我们得到了。

　　然后，我们保持一、二行不变，将1/3个第二行与第三行进行线性组合

　　可以自己写出需要左乘的矩阵吗？尝试着自己推导一下

　　你的结果是它吗 ？我们用E₂来表示这个矩阵。

　　经过这次变换，我们得到了我们想要的矩阵U：。

　　现在，我们可以用一个式子来表达消元的全过程了：

　　E₂(E₁A)=U

　　看到这里，可能有的强迫症患者或者完美主义者会发发牢骚：这个式子还是太过臃肿

　　所以

　　最后，我们合并消元步骤

　　我们想要的结果是类似于EA=U这样的干净整洁的式子，怎么做到呢？

　　在这里需要引入一条新的有关矩阵乘法的性质：矩阵乘法满足结合律（但不满足交换律）

　　换句话说，E₂(E₁A)=(E₂E₁)A。（但AB≠BA）

　　于是E=(E₂E₁)，我们管E叫做消元矩阵。

三、置换矩阵

　　此为附加内容

　行交换

　　我们消元时通过左乘矩阵实现了行与行的线性组合，那么，如果想要将两行进行交换，需要怎么做呢？

　　召唤个矩阵先：

　　假设我们想要这个矩阵的第一二行（得到）

　　对于新矩阵的第一行，我们相当于拿出了0个原矩阵的第一行，1个原矩阵的第二行，0个原矩阵的第三行。

　　对于新矩阵的第二行，我们相当于拿出了1个原矩阵的第一行，0个原矩阵的第二行，0个原矩阵的第三行。

　　对于新矩阵的第三行，我们相当于拿出了0个原矩阵的第一行，0个原矩阵的第二行，1个原矩阵的第三行。

　　因此，我们只需在原矩阵的基础上左乘一个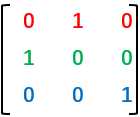。（各行颜色不同是为了便于理解其构成方式，没有其他特别含义）

　　我们管左乘的这个矩阵叫做置换矩阵，用P表示。

　列交换

　　之前提到过，左乘即操作行，右乘即操作列

　　召唤一个矩阵：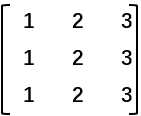

　　想要交换这个矩阵的第一二列，得到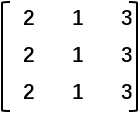

　　对于新矩阵的第一列，我们相当于拿出了0个原矩阵的第一列，1个原矩阵的第二列，0个原矩阵的第三列。

　　对于新矩阵的第二列，我们相当于拿出了1个原矩阵的第一列，0个原矩阵的第二列，0个原矩阵的第三列。

　　对于新矩阵的第三列，我们相当于拿出了0个原矩阵的第一列，0个原矩阵的第二列，1个原矩阵的第三列。

　　所以，只需要右乘

　　注意：这个矩阵虽然和上面交换行的置换矩阵长相相同，但性质与构成的方式却完全不同（行交换的置换矩阵是一行一行构成的，而列交换的却是一列一列构成的）

第二节、矩阵消元

标签：

原文地址：http://www.cnblogs.com/Dumblidor/p/5751579.html